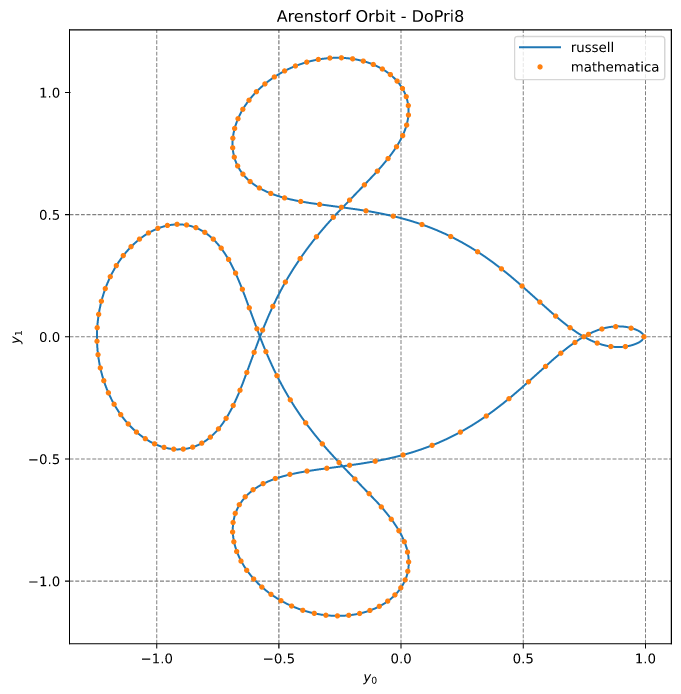14 个稳定版本
| 1.6.2 | 2024年7月23日 |
|---|---|
| 1.6.0 | 2024年5月21日 |
| 1.4.0 | 2024年4月30日 |
| 1.0.0 | 2024年3月30日 |
| 0.9.2 | 2024年3月17日 |
在 数学 中排名 #183
每月下载量 159
3MB
41K SLoC
Russell ODE - 常微分方程和微分代数方程求解器
该crate是Russell - Rust 科学库的一部分
内容
简介
此库(使用原生 Rust)实现了常微分方程(ODE)和微分代数方程(DAE)的求解器。具体来说,它实现了几种显式 Runge-Kutta 方法(例如,Dormand-Prince 公式)和两种隐式 Runge-Kutta 方法,即 Backward Euler 和五阶 Radau IIA(即 Radau5)。Radau5 求解器可以通过接受所谓的质量矩阵来解决索引为 1 的 DAE。
此库中的代码基于 Hairer-Nørsett-Wanner 书籍和相应的 Fortran 代码(见参考文献 [1] 和 [2])。然而,Dormand-Prince 5(4) 和 Dormand-Prince 8(5,3) 的实现与 Fortran 对应版本不同。Radau5 的代码紧密遵循参考文献 [2];然而,也考虑了一些细微的差异。尽管代码存在差异,数值结果与 Fortran 结果非常吻合。
推荐的方法是
DoPri5用于使用适度容忍度的 ODE 系统和非刚性问题DoPri8用于使用严格容忍度的 ODE 系统和非刚性问题Radau5用于可能刚性或非刚性的 ODE 和 DAE 系统以及适度到严格的容忍度
可以使用 System 数据结构轻松定义 ODE/DAE 系统;见下面的示例。
文档
参考文献
- Hairer E, Nørsett SP, Wanner G (2008) 常微分方程求解 I. 非刚性问题。第二版修订。2008年第三次印刷。Springer 计算数学系列,528页
- Hairer E, Wanner G (2002) 常微分方程求解 II. 刚性及微分代数问题。第二版修订。2002年第二次印刷。Springer 计算数学系列,614页
- Kreyszig E (2011) 高等工程数学;与Kreyszig H,Edward JN 合作,2011年第10版,新泽西州霍布肯,Wiley
安装
本crate依赖于一些非Rust的高性能库。有关安装这些依赖项的步骤,请参阅主要README文件
设置 Cargo.toml
👆检查crate版本并相应更新Cargo.toml
[dependencies]
russell_ode = "*"
可选特性
以下(Rust)功能可用
intel_mkl:使用Intel MKL代替OpenBLASlocal_suitesparse:使用本地编译的SuiteSparse版本with_mumps:启用MUMPS求解器(本地编译)
请注意,主要README文件展示了根据每个功能编译所需库的步骤。
🌟 示例
本节说明了如何使用russell_ode。另请参阅
单方程的简单常微分方程
使用Dormand-Prince 8(5,3)求解简单的ODE
dy
y' = —— = 1 with y(x=0)=0 thus y(x) = x
dx
请参阅代码simple_ode_single_equation.rs;如下所示复现
use russell_lab::{vec_approx_eq, StrError, Vector};
use russell_ode::prelude::*;
fn main() -> Result<(), StrError> {
// system
let ndim = 1;
let system = System::new(ndim, |f, x, y, _args: &mut NoArgs| {
f[0] = x + y[0];
Ok(())
});
// solver
let params = Params::new(Method::DoPri8);
let mut solver = OdeSolver::new(params, system)?;
// initial values
let x = 0.0;
let mut y = Vector::from(&[0.0]);
// solve from x = 0 to x = 1
let x1 = 1.0;
let mut args = 0;
solver.solve(&mut y, x, x1, None, &mut args)?;
println!("y =\n{}", y);
// check the results
let y_ana = Vector::from(&[f64::exp(x1) - x1 - 1.0]);
vec_approx_eq(&y, &y_ana, 1e-7);
// print stats
println!("{}", solver.stats());
Ok(())
}
输出如下
y =
┌ ┐
│ 0.718281815054018 │
└ ┘
DoPri8: Dormand-Prince method (explicit, order 8(5,3), embedded)
Number of function evaluations = 84
Number of performed steps = 7
Number of accepted steps = 7
Number of rejected steps = 0
Last accepted/suggested stepsize = 0.40139999999999776
Max time spent on a step = 7.483µs
Total time = 65.462µs
具有质量矩阵的简单系统
使用Radau5求解
y0' + y1' = -y0 + y1
y0' - y1' = y0 + y1
y2' = 1/(1 + x)
y0(0) = 1, y1(0) = 0, y2(0) = 0
因此
M y' = f(x, y)
使用
┌ ┐ ┌ ┐
│ 1 1 0 │ │ -y0 + y1 │
M = │ 1 -1 0 │ f = │ y0 + y1 │
│ 0 0 1 │ │ 1/(1 + x) │
└ ┘ └ ┘
雅可比矩阵是
┌ ┐
df │ -1 1 0 │
J = —— = │ 1 1 0 │
dy │ 0 0 0 │
└ ┘
解析解是
y0(x) = cos(x)
y1(x) = -sin(x)
y2(x) = log(1 + x)
请参阅代码simple_system_with_mass.rs;如下所示复现
use russell_lab::{vec_approx_eq, StrError, Vector};
use russell_ode::prelude::*;
use russell_sparse::{CooMatrix, Sym};
fn main() -> Result<(), StrError> {
// ODE system
let ndim = 3;
let jac_nnz = 4;
let mut system = System::new(ndim, |f: &mut Vector, x: f64, y: &Vector, _args: &mut NoArgs| {
f[0] = -y[0] + y[1];
f[1] = y[0] + y[1];
f[2] = 1.0 / (1.0 + x);
Ok(())
});
// function to compute the Jacobian matrix
let symmetric = Sym::No;
system.set_jacobian(
Some(jac_nnz),
symmetric,
move |jj: &mut CooMatrix, alpha: f64, _x: f64, _y: &Vector, _args: &mut NoArgs| {
jj.reset();
jj.put(0, 0, alpha * (-1.0))?;
jj.put(0, 1, alpha * (1.0))?;
jj.put(1, 0, alpha * (1.0))?;
jj.put(1, 1, alpha * (1.0))?;
Ok(())
},
)?;
// mass matrix
let mass_nnz = 5;
system.set_mass(Some(mass_nnz), symmetric, |mm: &mut CooMatrix| {
mm.put(0, 0, 1.0).unwrap();
mm.put(0, 1, 1.0).unwrap();
mm.put(1, 0, 1.0).unwrap();
mm.put(1, 1, -1.0).unwrap();
mm.put(2, 2, 1.0).unwrap();
})?;
// solver
let params = Params::new(Method::Radau5);
let mut solver = OdeSolver::new(params, system)?;
// initial values
let x = 0.0;
let mut y = Vector::from(&[1.0, 0.0, 0.0]);
// solve from x = 0 to x = 20
let x1 = 20.0;
let mut args = 0;
solver.solve(&mut y, x, x1, None, &mut args)?;
println!("y =\n{}", y);
// check the results
let y_ana = Vector::from(&[f64::cos(x1), -f64::sin(x1), f64::ln(1.0 + x1)]);
vec_approx_eq(&y, &y_ana, 1e-3);
// print stats
println!("{}", solver.stats());
Ok(())
}
输出如下
y =
┌ ┐
│ 0.40864108577398206 │
│ -0.9136567566808349 │
│ 3.044521229909652 │
└ ┘
Radau5: Radau method (Radau IIA) (implicit, order 5, embedded)
Number of function evaluations = 203
Number of Jacobian evaluations = 1
Number of factorizations = 8
Number of lin sys solutions = 52
Number of performed steps = 46
Number of accepted steps = 46
Number of rejected steps = 0
Number of iterations (maximum) = 2
Number of iterations (last step) = 1
Last accepted/suggested stepsize = 0.5055117216674699
Max time spent on a step = 40.817µs
Max time spent on the Jacobian = 558ns
Max time spent on factorization = 199.895µs
Max time spent on lin solution = 53.101µs
Total time = 2.653323ms
Brusselator 常微分方程
本例对应于参考#1第116页的图16.4。问题定义在参考#1第116页的方程(16.12)中。
该系统是
y0' = 1 - 4 y0 + y0² y1
y1' = 3 y0 - y0² y1
with y0(x=0) = 3/2 and y1(x=0) = 3
雅可比矩阵是
┌ ┐
df │ -4 + 2 y0 y1 y0² │
J = —— = │ │
dy │ 3 - 2 y0 y1 -y0² │
└ ┘
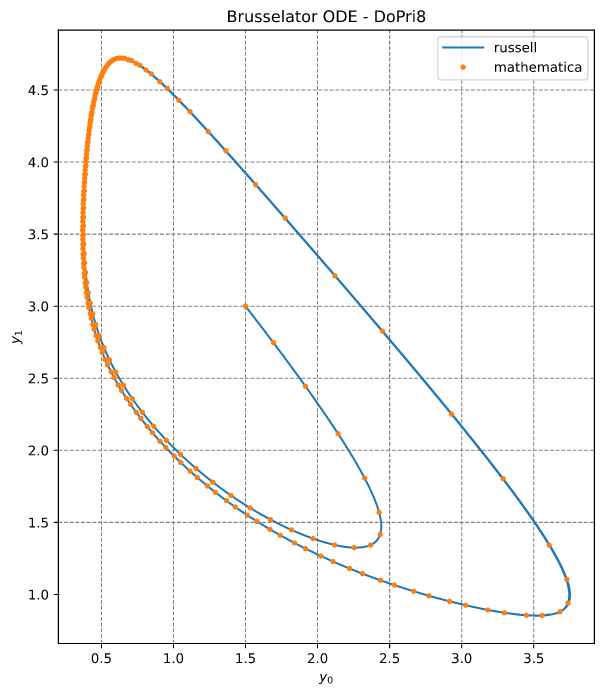
使用 DoPri8 -- 8(5,3) -- 稠密输出的求解
这是一个由两个ODE组成的系统,在参考#1中有很好的解释。这个问题使用DoPri8方法求解(它有一个5阶和3阶的混合误差估计器;见参考#1)。
本例还展示了如何启用密集输出。
请参阅代码brusselator_ode_dopri8.rs;如下所示复现(不带绘图命令)
输出如下
y_russell = [0.4986435155366857, 4.596782273713258]
y_mathematica = [0.49863707126834783, 4.596780349452011]
DoPri8: Dormand-Prince method (explicit, order 8(5,3), embedded)
Number of function evaluations = 647
Number of performed steps = 45
Number of accepted steps = 38
Number of rejected steps = 7
Last accepted/suggested stepsize = 2.1617616186304227
Max time spent on a step = 47.643µs
Total time = 898.347µs
以下显示了(密集)解的图像
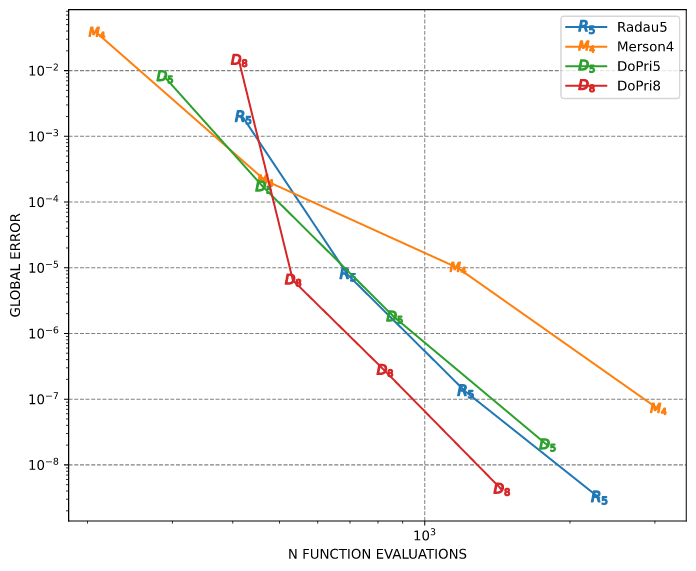
可变步长
本例使用不同容忍度求解Brusselator ODE的可变步长。在本例中,tol = abs_tol = rel_tol。全局误差是Russell的结果与使用高精度获得的Mathematica的结果之间的差异。Mathematica代码是
Needs["DifferentialEquations`NDSolveProblems`"];
Needs["DifferentialEquations`NDSolveUtilities`"];
sys = GetNDSolveProblem["BrusselatorODE"];
sol = NDSolve[sys, Method -> "StiffnessSwitching", WorkingPrecision -> 32];
ref = First[FinalSolutions[sys, sol]]
请参阅代码brusselator_ode_var_step.rs
结果如下
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
tol = 1.00E-02 1.00E-04 1.00E-06 1.00E-08
Method Error Error Error Error
────────────────────────────────────────────────────
Radau5 1.9E-03 7.9E-06 1.3E-07 3.2E-09
Merson4 3.8E-02 2.1E-04 9.9E-06 7.1E-08
DoPri5 8.0E-03 1.7E-04 1.8E-06 2.0E-08
DoPri8 1.4E-02 6.4E-06 2.7E-07 4.2E-09
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
收敛图如下
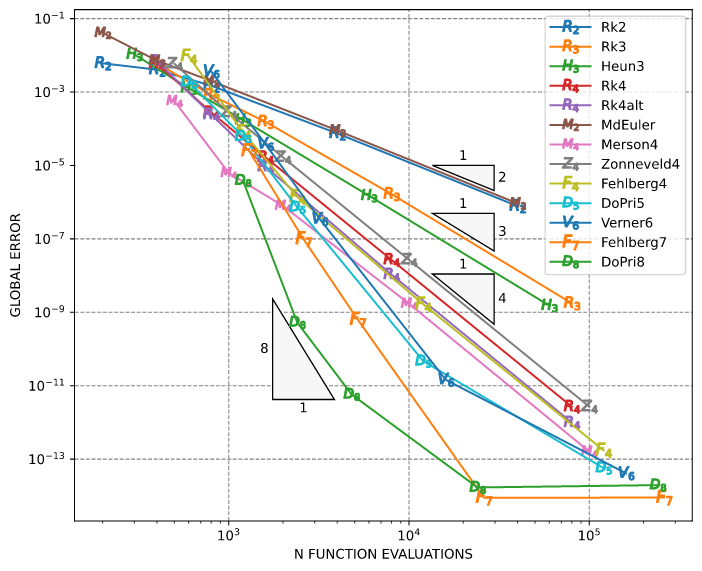
固定步长
本例使用固定步长和显式Runge-Kutta方法求解Brusselator ODE。全局误差也与上一节中的Russell和Mathematica的差异一样。
请参阅代码brusselator_ode_fix_step.rs
结果如下
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
h = 2.00E-01 1.00E-01 5.00E-02 1.00E-02 1.00E-03
Method Error Error Error Error Error
────────────────────────────────────────────────────────
Rk2 6.1E-03 4.1E-03 1.5E-03 7.4E-05 7.8E-07
Rk3 6.1E-03 8.2E-04 1.5E-04 1.7E-06 1.8E-09
Heun3 1.1E-02 1.3E-03 1.7E-04 1.5E-06 1.5E-09
Rk4 5.9E-03 2.8E-04 1.7E-05 2.7E-08 2.7E-12
Rk4alt 7.0E-03 2.4E-04 9.3E-06 1.1E-08 9.9E-13
MdEuler 4.1E-02 7.2E-03 2.0E-03 9.0E-05 9.2E-07
Merson4 5.7E-04 6.3E-06 7.9E-07 1.7E-09 1.6E-13
Zonneveld4 5.9E-03 2.8E-04 1.7E-05 2.7E-08 2.7E-12
Fehlberg4 9.4E-03 8.1E-05 1.4E-06 1.7E-09 1.7E-13
DoPri5 1.9E-03 6.1E-05 7.3E-07 4.7E-11 5.7E-14
Verner6 3.6E-03 3.8E-05 3.5E-07 1.4E-11 4.1E-14
Fehlberg7 2.5E-05 9.9E-08 6.3E-10 8.9E-15 8.9E-15
DoPri8 3.9E-06 5.3E-10 5.8E-12 1.7E-14 2.0E-14
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
收敛图如下
Brusselator 偏微分方程
本例对应于参考文献#1第250页和第251页的图10.4(a,b)。问题在参考文献#1的第248页和第249页的公式(10.10-10.14)中定义。
如果second_book为真,则此例对应于参考文献#2第151页的图10.7。此外,在这种情况下,问题在参考文献#2的第151页和第152页的公式(10.15-10.16)中定义。
在第一本书中,边界条件是Neumann类型,而在第二本书中,边界条件是周期性的。此外,第二本书中的初始值与第一本书中的不同。
模型如下所示
∂u ⎛ ∂²u ∂²u ⎞
——— = 1 - 4.4 u + u² v + α ⎜ ——— + ——— ⎟ + I(t,x,y)
∂t ⎝ ∂x² ∂y² ⎠
∂v ⎛ ∂²v ∂²v ⎞
——— = 3.4 u - u² v + α ⎜ ——— + ——— ⎟
∂t ⎝ ∂x² ∂y² ⎠
with: t ≥ 0, 0 ≤ x ≤ 1, 0 ≤ y ≤ 1
其中I(t,x,y)是不均匀函数(第二本书),由以下公式给出
⎧ 5 if (x-0.3)²+(y-0.6)² ≤ 0.1² and t ≥ 1.1
I(t,x,y) = ⎨
⎩ 0 otherwise
第一本书考虑以下Neumann边界条件
∂u ∂v
——— = 0 ——— = 0
→ →
∂n ∂n
以及以下初始条件(第一本书)
u(t=0,x,y) = 0.5 + y v(t=0,x,y) = 1 + 5 x
第二本书考虑对u的周期性边界条件。然而,在这里我们假设对u和v都是周期性的
u(t, 0, y) = u(t, 1, y)
u(t, x, 0) = u(t, x, 1)
v(t, 0, y) = v(t, 1, y) ← Not in the book
v(t, x, 0) = v(t, x, 1) ← Not in the book
第二本书考虑以下初始条件
u(0, x, y) = 22 y pow(1 - y, 1.5)
v(0, x, y) = 27 x pow(1 - x, 1.5)
标量场u(x, y)和v(x, y)被映射到一个矩形网格上,其离散对应物由以下表示
pᵢⱼ(t) := u(t, xᵢ, yⱼ)
qᵢⱼ(t) := v(t, xᵢ, yⱼ)
因此,ndim = 2 npoint²,其中npoint是x或y线上点的数量。
使用有限差分法(FDM)对x和y上的二阶偏导数(拉普拉斯算子)进行近似。
将pᵢⱼ和qᵢⱼ的值映射到向量U和V上,如下所示
pᵢⱼ → Uₘ
qᵢⱼ → Vₘ
with m = i + j nx
然后,它们被存储在一个单独的向量Y中
┌ ┐
│ U │
Y = │ │
│ V │
└ ┘
因此
Uₘ = Yₘ and Vₘ = Yₛ₊ₘ
where 0 ≤ m ≤ s - 1 and (shift) s = npoint²
就分量而言,我们可以写成
⎧ Uₐ if a < s
Yₐ = ⎨
⎩ Vₐ₋ₛ if a ≥ s
where 0 ≤ a ≤ ndim - 1 and ndim = 2 s
方程组的分量由以下定义:(撇号表示时间导数;对重复索引不进行求和)
Uₘ' = 1 - 4.4 Uₘ + Uₘ² Vₘ + Σ Aₘₖ Uₖ
k
Vₘ' = 3.4 Uₘ - Uₘ² Vₘ + Σ Aₘₖ Uₖ
k
where Aₘₖ are the elements of the discrete Laplacian matrix
构建雅可比矩阵的分量如下:(对重复索引不进行求和)
∂Uₘ'
———— = -4.4 δₘₙ + 2 Uₘ δₘₙ Vₘ + Aₘₙ
∂Uₙ
∂Uₘ'
———— = Uₘ² δₘₙ
∂Vₙ
∂Vₘ'
———— = 3.4 δₘₙ - 2 Uₘ δₘₙ Vₘ
∂Uₙ
∂Vₘ'
———— = -Uₘ² δₘₙ + Aₘₙ
∂Vₙ
where δₘₙ is the Kronecker delta
使用Fₐ := ∂Yₐ/∂t,雅可比矩阵的分量可以如下“组装”
⎧ ⎧ ∂Uₐ'/∂Uₑ if e < s
│ ⎨ if a < s
∂Fₐ │ ⎩ ∂Uₐ'/∂Vₑ₋ₛ if e ≥ s
——— = ⎨
∂Yₑ │ ⎧ ∂Vₐ₋ₛ'/∂Uₑ if e < s
│ ⎨ if a ≥ s
⎩ ⎩ ∂Vₐ₋ₛ'/∂Vₑ₋ₛ if e ≥ s
where 0 ≤ a ≤ ndim - 1 and 0 ≤ e ≤ ndim - 1
第一本书
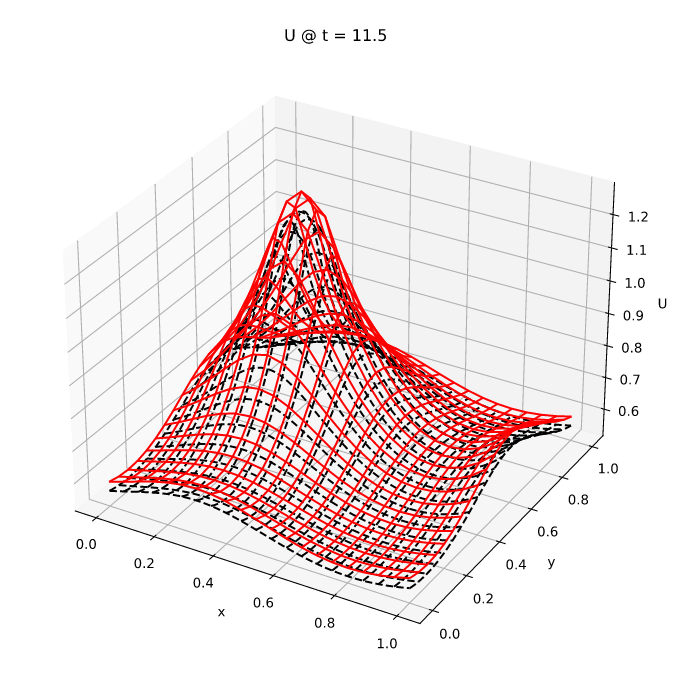
我们使用Radau5求解此问题。使用npoint = 21生成近似解,并在brusselator_pde_radau5.rs中实现,该文件位于此处。此代码将为每个(密集)输出时间生成一系列文件,每个文件对应一个,h_out = 0.5。
然后可以使用brusselator_pde_plot.rs绘制结果
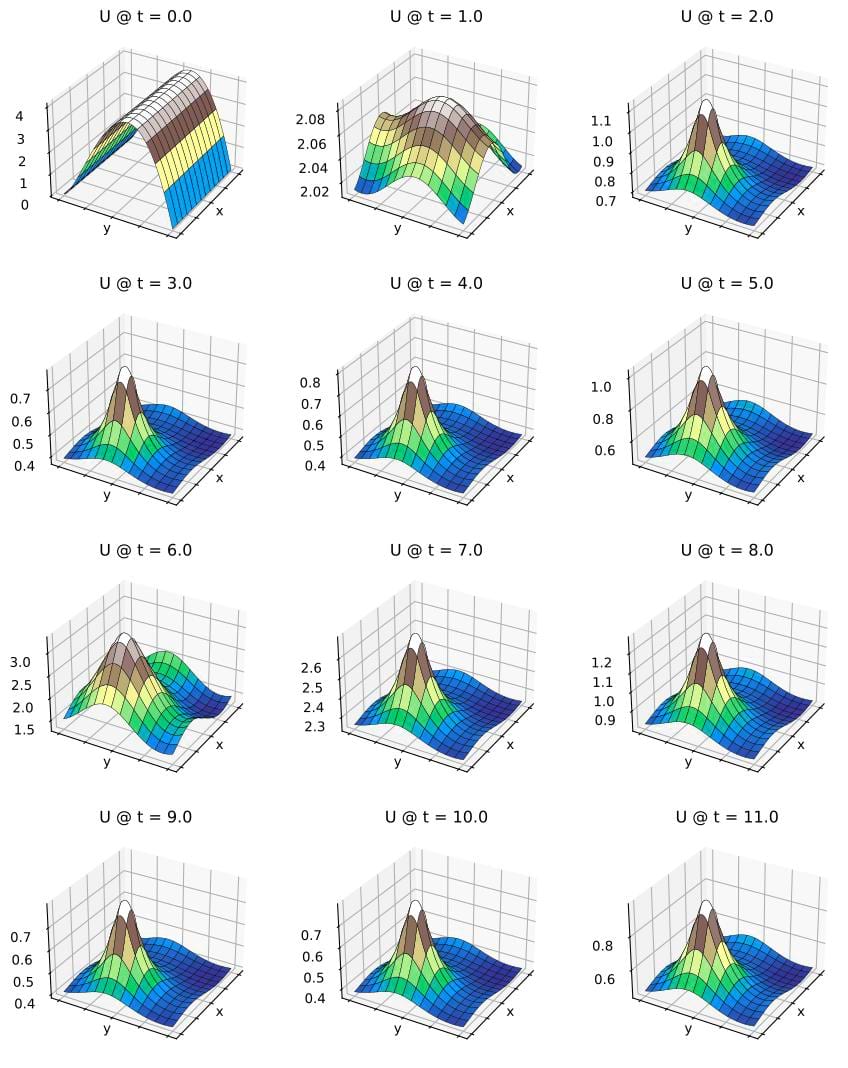
以下为U场的图形结果
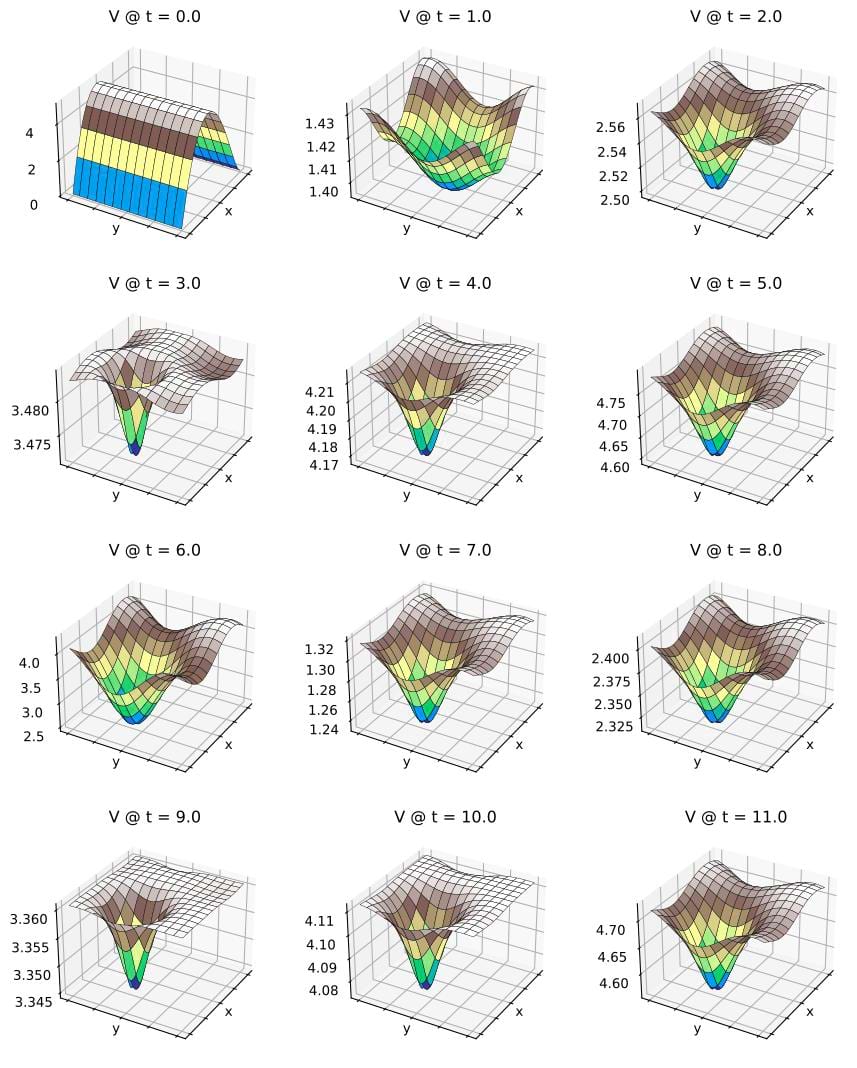
以下为V场的图形结果
这些图与参考文献#1第250页和第251页上的对应图非常吻合。
使用russell的计算结果也与使用Mathematica获得的结果进行比较。验证在test_radau5_brusselator_pde中实现,该文件位于此处。
以下图显示了russell(黑色虚线)和Mathematica(红色实线)对U场的计算结果
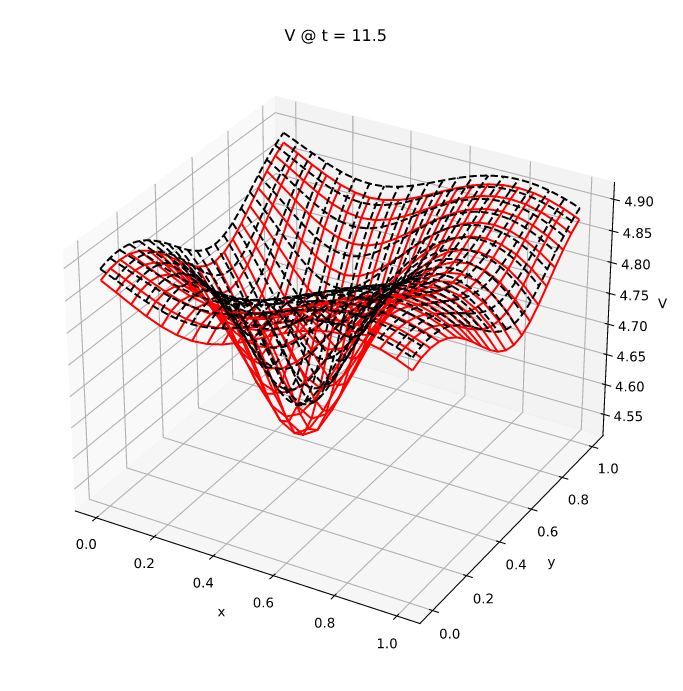
以下图显示了russell(黑色虚线)和Mathematica(红色实线)对V场的计算结果
第二本书
对于第二本书中的问题,我们运行了brusselator_pde_radau5_2nd.rs,其中npoint = 129和h_out = 1.0。
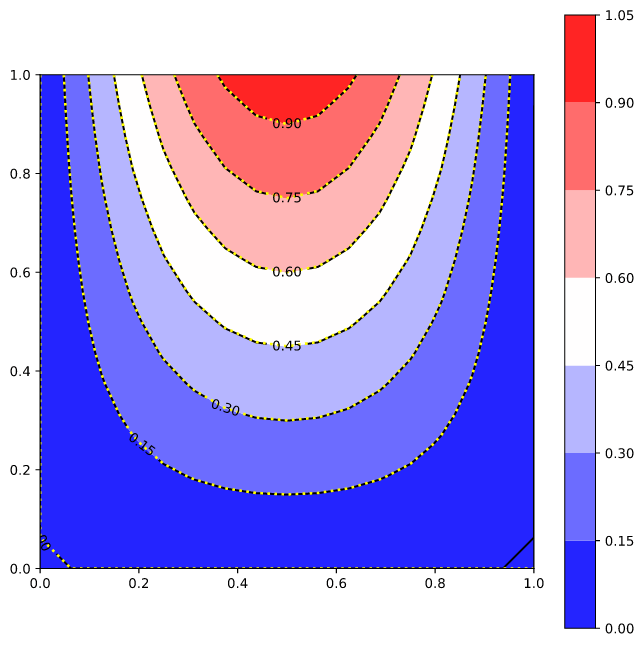
以下为U场的图形结果
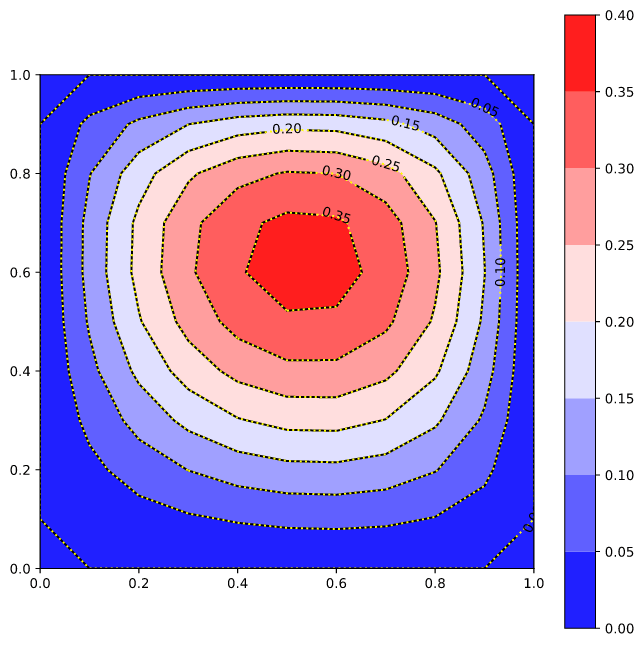
以下为V场的图形结果
代码brusselator_pde_2nd_comparison.rs将russell的结果与Mathematica的结果进行比较。
以下图显示了russell(黑色虚线)和Mathematica(红色实线)对U场的计算结果
以下图显示了russell(黑色虚线)和Mathematica(红色实线)对V场的计算结果
Arenstorf 轨道
本例与参考#1第130页的图0.1相对应。该问题在参考#1第129页和第130页的方程(0.1)和(0.2)中定义。
从Hairer-Nørsett-Wanner
"(...) 来自天文学的例子,限制性三体问题。(...) 质量为μ' = 1 − μ和μ的两个物体在一个平面上做圆周运动,第三个质量可忽略不计的物体在同一平面上运动。(...)"
系统方程为
y0'' = y0 + 2 y1' - μ' (y0 + μ) / d0 - μ (y0 - μ') / d1
y1'' = y1 - 2 y0' - μ' y1 / d0 - μ y1 / d1
赋值如下
y2 := y0' ⇒ y2' = y0''
y3 := y1' ⇒ y3' = y1''
我们得到一个4维问题
f0 := y0' = y2
f1 := y1' = y3
f2 := y2' = y0 + 2 y3 - μ' (y0 + μ) / d0 - μ (y0 - μ') / d1
f3 := y3' = y1 - 2 y2 - μ' y1 / d0 - μ y1 / d1
代码输出为
y_russell = [0.9943002573065823, 0.000505756322923528, 0.07893182893575335, -1.9520617089599261]
y_mathematica = [0.9939999999999928, 2.4228439406717e-14, 3.6631563591513e-12, -2.0015851063802006]
DoPri8: Dormand-Prince method (explicit, order 8(5,3), embedded)
Number of function evaluations = 870
Number of performed steps = 62
Number of accepted steps = 47
Number of rejected steps = 15
Last accepted/suggested stepsize = 0.005134142939114363
Max time spent on a step = 10.538µs
Total time = 1.399021ms
结果如下所示
Hairer-Wanner 方程 (1.1)
本例与参考#2第2页的图1.1和图1.2相对应。该问题在参考#2第2页的方程(1.1)中定义。
该系统是
y0' = -50 (y0 - cos(x))
with y0(x=0) = 0
雅可比矩阵是
df ┌ ┐
J = —— = │ -50 │
dy └ ┘
本例说明了当步长超过稳定性极限时,前向Euler方法的稳定性。方程如下(参考#2,第2页)
本例还展示了如何启用接受步骤的输出。
结果如下所示
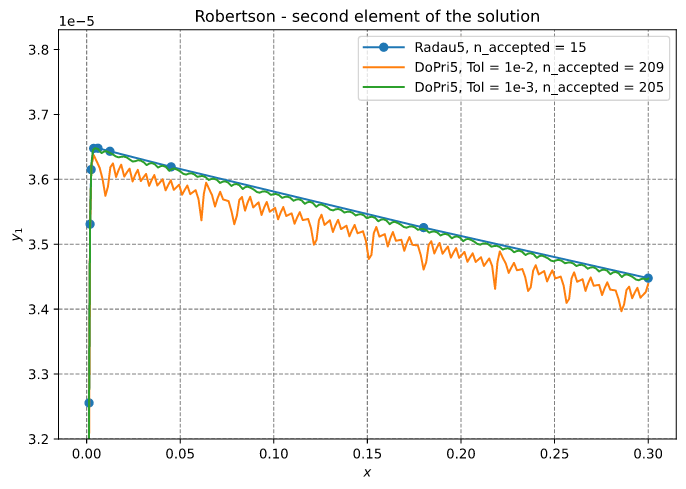
Robertson 方程
本例与参考#2第4页的图1.3相对应。该问题在参考#2第3页的方程(1.4)中定义。
该系统是
y0' = -0.04 y0 + 1.0e4 y1 y2
y1' = 0.04 y0 - 1.0e4 y1 y2 - 3.0e7 y1²
y2' = 3.0e7 y1²
with y0(0) = 1, y1(0) = 0, y2(0) = 0
本例说明了Robertson方程。在此问题中,DoPri5使用许多步骤(大约200步)。另一方面,Radau5使用17个接受步骤解决了该问题。
本例还展示了如何启用接受步骤的输出。
参见代码robertson.rs
使用两组容差,用Radau5和DoPri5近似求解。
输出如下
Radau5: Radau method (Radau IIA) (implicit, order 5, embedded)
Number of function evaluations = 88
Number of Jacobian evaluations = 8
Number of factorizations = 15
Number of lin sys solutions = 24
Number of performed steps = 17
Number of accepted steps = 15
Number of rejected steps = 1
Number of iterations (maximum) = 2
Number of iterations (last step) = 1
Last accepted/suggested stepsize = 0.8160578540023586
Max time spent on a step = 117.916µs
Max time spent on the Jacobian = 1.228µs
Max time spent on factorization = 199.151µs
Max time spent on lin solution = 56.767µs
Total time = 1.922108ms
Tol = 1e-2
DoPri5: Dormand-Prince method (explicit, order 5(4), embedded)
Number of function evaluations = 1585
Number of performed steps = 264
Number of accepted steps = 209
Number of rejected steps = 55
Last accepted/suggested stepsize = 0.0017137362591141277
Max time spent on a step = 2.535µs
Total time = 2.997516ms
Tol = 1e-3
DoPri5: Dormand-Prince method (explicit, order 5(4), embedded)
Number of function evaluations = 1495
Number of performed steps = 249
Number of accepted steps = 205
Number of rejected steps = 44
Last accepted/suggested stepsize = 0.0018175194753331549
Max time spent on a step = 1.636µs
Total time = 3.705391ms
结果如下所示
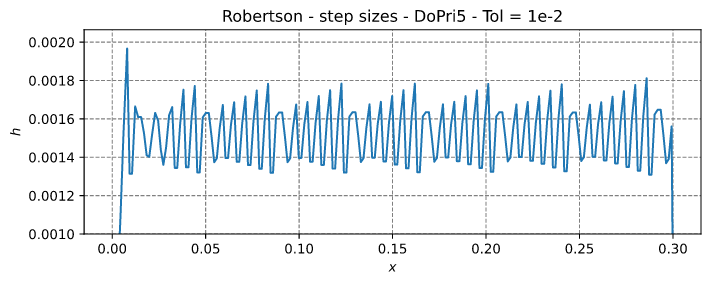
DoPri解的步长如下所示(Tol = 1e-2)
Van der Pol 方程
本例与参考#2第5页的方程(1.5')相对应。
该系统是
y0' = y1
y1' = ((1.0 - y[0] * y[0]) * y[1] - y[0]) / ε
其中ε定义了问题的刚度 + 条件(方程 + 初始条件 + 步长 + 方法)。
DoPri5
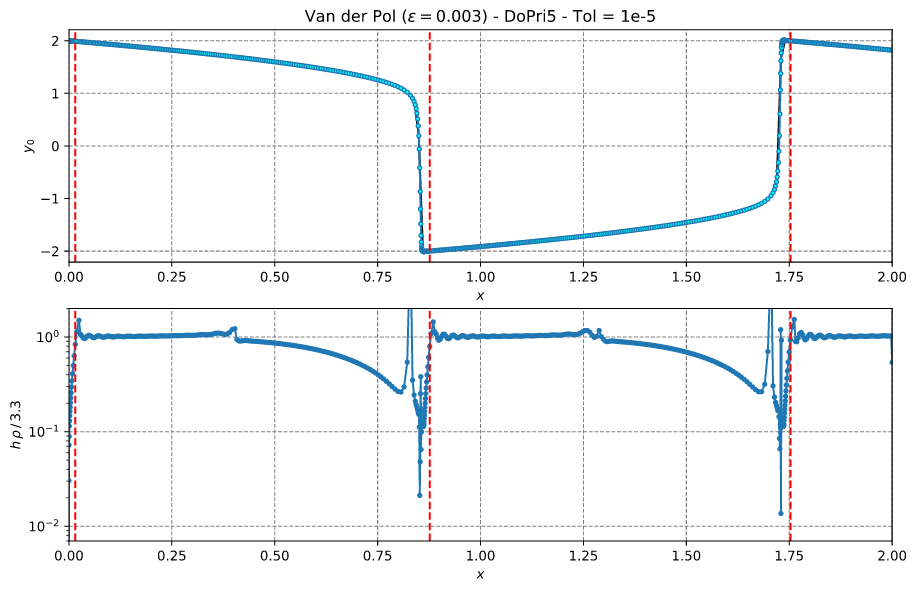
本例与参考#2第23页的图2.6相对应。该问题在参考#2第5页的方程(1.5')中定义。
本例说明了ε = 0.003的Van der Pol问题的刚度。在此示例中,使用Tol = 1e-3的DoPri5。
本例还展示了如何启用刚度检测。
输出如下所示
y =
┌ ┐
│ 1.819918013289893 │
│ -0.7863062155442466 │
└ ┘
DoPri5: Dormand-Prince method (explicit, order 5(4), embedded)
Number of function evaluations = 3133
Number of performed steps = 522
Number of accepted steps = 498
Number of rejected steps = 24
Last accepted/suggested stepsize = 0.004363549192919735
Max time spent on a step = 2.558µs
Total time = 1.715917ms
结果如下所示
图中红色虚线标记了首次检测到刚度的时刻。经过15个接受步骤并重复达到刚度阈值后,确认刚度。当h·ρ大于相应的因子·max(h·ρ)---稳定性极限的值(DoPri5为3.3;因子约为0.976)时,计算正阈值。请注意,ρ是Jacobian的主特征值的近似。经过6个接受步骤,如果没有达到阈值,则刚度检测标志设置为false。
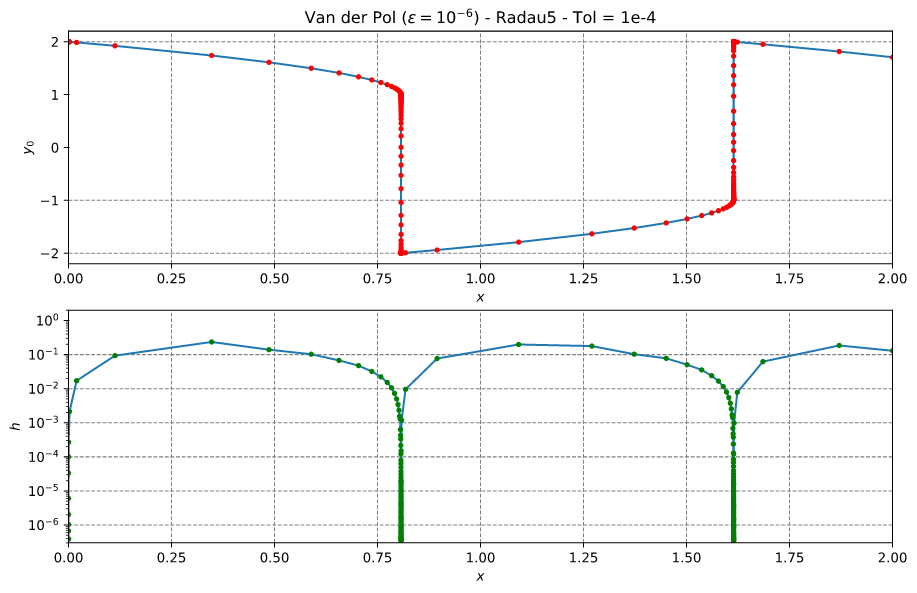
Radau5
本例与参考#2第125页的图8.1相对应。该问题在参考#2第5页的方程(1.5')中定义。
本例使用了较小的 ε = 1e-6,这使得问题 + 条件变得非常刚性。它使用 Radau5 求解器进行求解,该求解器可以很好地处理刚性问题。请注意,DoPri5 除非考虑了非常高的步数(以及阶数配置),否则不会使用如此小的 ε 来解决这个问题。
输出如下所示
y =
┌ ┐
│ 1.7061626037853908 │
│ -0.892799551109113 │
└ ┘
Radau5: Radau method (Radau IIA) (implicit, order 5, embedded)
Number of function evaluations = 2237
Number of Jacobian evaluations = 160
Number of factorizations = 252
Number of lin sys solutions = 663
Number of performed steps = 280
Number of accepted steps = 241
Number of rejected steps = 7
Number of iterations (maximum) = 6
Number of iterations (last step) = 3
Last accepted/suggested stepsize = 0.2466642610579514
Max time spent on a step = 136.487µs
Max time spent on the Jacobian = 949ns
Max time spent on factorization = 223.917µs
Max time spent on lin solution = 4.010536ms
Total time = 37.8697ms
结果如下所示
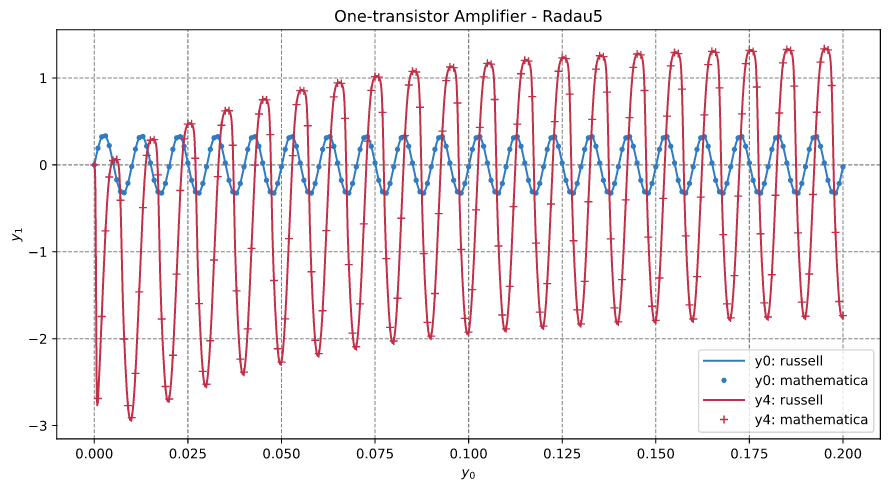
单晶体管放大器
本例对应于参考 #2 第 377 页的图 1.3 和第 379 页的图 1.4。问题在参考 #2 第 377 页的公式 (1.14) 中定义。
这是一个建模一晶体管放大器节点电压的微分代数问题。
DAE 以所谓的 质量矩阵 形式表示(ndim = 5)
M y' = f(x, y)
with: y0(0)=0, y1(0)=Ub/2, y2(0)=Ub/2, y3(0)=Ub, y4(0)=0
其中右手边函数的元素是
f0 = (y0 - ue) / R
f1 = (2 y1 - UB) / S + γ g12
f2 = y2 / S - g12
f3 = (y3 - UB) / S + α g12
f4 = y4 / S
with:
ue = A sin(ω x)
g12 = β (exp((y1 - y2) / UF) - 1)
与公式 (1.14) 相比,我们将所有电阻 Rᵢ 设置为 S,除了第一个(R := R₀)。
质量矩阵是
┌ ┐
│ -C1 C1 │
│ C1 -C1 │
M = │ -C2 │
│ -C3 C3 │
│ C3 -C3 │
└ ┘
雅可比矩阵是
┌ ┐
│ 1/R │
│ 2/S + γ h12 -γ h12 │
J = │ -h12 1/S + h12 │
│ α h12 -α h12 │
│ 1/S │
│ 1/S │
└ ┘
with:
h12 = β exp((y1 - y2) / UF) / UF
注意: 在这个库中,只有 Radau5 可以求解这样的 DAE。
请参阅代码 amplifier1t_radau5.rs
输出如下所示
y_russell = [-0.022267, 3.068709, 2.898349, 1.499405, -1.735090]
y_mathematica = [-0.022267, 3.068709, 2.898349, 1.499439, -1.735057]
Radau5: Radau method (Radau IIA) (implicit, order 5, embedded)
Number of function evaluations = 6007
Number of Jacobian evaluations = 480
Number of factorizations = 666
Number of lin sys solutions = 1840
Number of performed steps = 666
Number of accepted steps = 481
Number of rejected steps = 39
Number of iterations (maximum) = 6
Number of iterations (last step) = 1
Last accepted/suggested stepsize = 0.00007705697843645314
Max time spent on a step = 55.281µs
Max time spent on the Jacobian = 729ns
Max time spent on factorization = 249.11µs
Max time spent on lin solution = 241.201µs
Total time = 97.951021ms
结果如下所示
PDE:2D 中的离散拉普拉斯算子
为了方便(例如,在基准测试中),russell_ode 实现了一个基于有限差分法(FDM)的离散拉普拉斯算子(2D)。
此算子可用于解决简单的偏微分方程(PDE)问题。
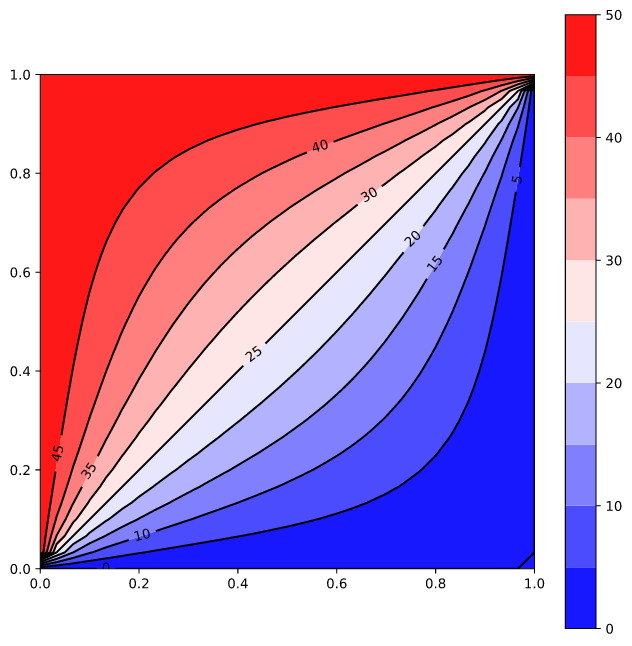
拉普拉斯方程
使用有限差分法(FDM)近似求解以下在 (1.0 × 1.0) 矩形上的解
∂²ϕ ∂²ϕ
——— + ——— = 0
∂x² ∂y²
具有以下基本(Dirichlet)边界条件
left: ϕ(0.0, y) = 50.0
right: ϕ(1.0, y) = 0.0
bottom: ϕ(x, 0.0) = 0.0
top: ϕ(x, 1.0) = 50.0
请参阅代码 pde_laplace_equation.rs
结果如下所示
泊松方程 1
使用有限差分法(FDM)近似求解以下在 (1.0 × 1.0) 矩形上的解
∂²ϕ ∂²ϕ
——— + ——— = 2 x (y - 1) (y - 2 x + x y + 2) exp(x - y)
∂x² ∂y²
在 (1.0 × 1.0) 正方形上,具有齐次边界条件。
解析解是
ϕ(x, y) = x y (x - 1) (y - 1) exp(x - y)
请参阅代码 test_pde_poisson_1.rs
结果如下所示
泊松方程 2
使用有限差分法(FDM)近似求解以下在 (1.0 × 1.0) 矩形上的解
∂²ϕ ∂²ϕ
——— + ——— = - π² y sin(π x)
∂x² ∂y²
在 (1.0 × 1.0) 正方形上,具有以下基本边界条件
left: ϕ(0.0, y) = 0.0
right: ϕ(1.0, y) = 0.0
bottom: ϕ(x, 0.0) = 0.0
top: ϕ(x, 1.0) = sin(π x)
解析解是
ϕ(x, y) = y sin(π x)
参考:Olver PJ (2020) - 第 210 页 - 偏微分方程导论,Springer
请参阅代码 test_pde_poisson_2.rs
结果如下所示
泊松方程 3
使用有限差分法(FDM)近似求解以下在 (1.0 × 1.0) 矩形上的解
∂²ϕ ∂²ϕ
——— + ——— = source(x, y)
∂x² ∂y²
在 (1.0 × 1.0) 正方形上,具有齐次基本边界条件
源项由以下给出(对于人工解)
source(x, y) = 14y³ - (16 - 12x) y² - (-42x² + 54x - 2) y + 4x³ - 16x² + 12x
解析解是
ϕ(x, y) = x (1 - x) y (1 - y) (1 + 2x + 7y)
请参阅代码 test_pde_poisson_3.rs
结果如下所示
依赖项
~3–4MB
~77K SLoC