8个版本 (2个稳定版)
| 2.0.2 | 2024年6月18日 |
|---|---|
| 2.0.1 | 2024年6月5日 |
| 0.1.5 | 2023年10月6日 |
| 0.1.4 | 2023年9月6日 |
| 0.1.1 | 2023年8月12日 |
#165 in 数学
每月下载量 445次
1MB
256 行
RayBNN_DiffEq
基于CUDA、OpenCL和oneAPI使用GPU、CPU和FPGA进行微分方程求解
需要Arrayfire和Arrayfire Rust
支持f16、f32、f64、Complexf16、Complexf32、Complexf64
还支持矩阵微分方程和稀疏矩阵微分方程
矩阵大小可达100000x100000
安装Arrayfire
在https://arrayfire.com/binaries/安装Arrayfire 3.9.0的二进制文件
或从源代码构建https://github.com/arrayfire/arrayfire/wiki/Getting-ArrayFire
首次运行Arrayfire可能会比较慢,因为它需要编译CUDA和OpenCL内核。后续运行将更快。
添加到您的Cargo.toml
arrayfire = { version = "3.8.1", package = "arrayfire_fork" }
num = "0.4.1"
num-traits = "0.2.16"
half = { version = "2.3.1" , features = ["num-traits"] }
RayBNN_DataLoader = "2.0.3"
RayBNN_DiffEq = "2.0.2"
示例列表
- 使用CUDA f64的线性常微分方程
- 使用CUDA f64的3x3线性矩阵常微分方程
- 使用CUDA f64的1000x1000线性矩阵常微分方程
- 使用CUDA f32的线性常微分方程
- 插值求解结果
- 在CPU、OpenCL和CUDA之间选择
使用Float 64位精度在CUDA上求解简单线性常微分方程
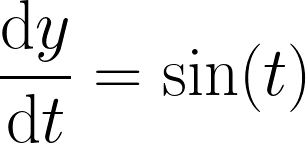
//cargo run --example Linear_ODE --release
use arrayfire;
use RayBNN_DiffEq;
//Select CUDA and GPU Device 0
const BACK_END: arrayfire::Backend = arrayfire::Backend::CUDA;
const DEVICE: i32 = 0;
fn main() {
arrayfire::set_backend(BACK_END);
arrayfire::set_device(DEVICE);
// Set the Linear Differentail Equation
// dy/dt = sin(t)
let diffeq = |t: &arrayfire::Array<f64>, y: &arrayfire::Array<f64>| -> arrayfire::Array<f64> {
arrayfire::sin(&t)
};
//Start at t=0 and end at t=1000
//Step size of 0.001
//Relative error of 1E-9
//Absolute error of 1E-9
//Error Type compute the total error of every element in y
let options: RayBNN_DiffEq::ODE::ODE45::ODE45_Options<f64> = RayBNN_DiffEq::ODE::ODE45::ODE45_Options {
tstart: 0.0f64,
tend: 1000.0f64,
tstep: 0.001f64,
rtol: 1.0E-9f64,
atol: 1.0E-9f64,
error_select: RayBNN_DiffEq::ODE::ODE45::error_type::TOTAL_ERROR
};
let t_dims = arrayfire::Dim4::new(&[1,1,1,1]);
let mut t = arrayfire::constant::<f64>(0.0,t_dims);
let y0_dims = arrayfire::Dim4::new(&[1,1,1,1]);
let mut y = arrayfire::constant::<f64>(0.0,y0_dims);
let mut dydt = arrayfire::constant::<f64>(0.0,y0_dims);
//Initial Point of Differential Equation
//Set y(t=0) = 1.0
let y0 = arrayfire::constant::<f64>(1.0,y0_dims);
println!("Running");
arrayfire::sync(DEVICE);
let starttime = std::time::Instant::now();
//Run Solver
RayBNN_DiffEq::ODE::ODE45::solve(
&y0
,diffeq
,&options
,&mut t
,&mut y
,&mut dydt
);
arrayfire::sync(DEVICE);
let elapsedtime = starttime.elapsed();
arrayfire::sync(DEVICE);
arrayfire::print_gen("y".to_string(), &y,Some(6));
arrayfire::print_gen("t".to_string(), &t,Some(6));
println!("Computed {} Steps In: {:.6?}", y.dims()[1],elapsedtime);
//Error Analysis
let actualy = 2.0f64 - arrayfire::cos(&t);
let error = y - actualy;
//arrayfire::print_gen("error".to_string(), &error,Some(6));
}
Computed 11704 Steps In: 4.623646s
使用Float 64位精度在CUDA上求解3x3矩阵线性常微分方程
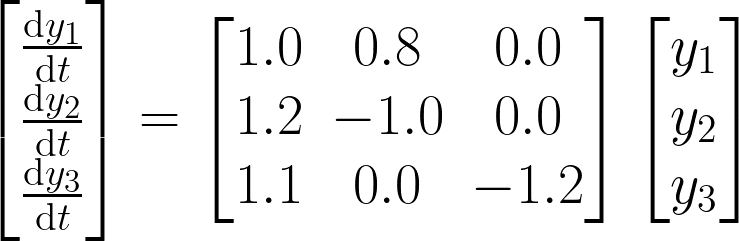
//cargo run --example Linear_Matrix_ODE --release
use arrayfire;
use RayBNN_DiffEq;
//Select CUDA and GPU Device 0
const BACK_END: arrayfire::Backend = arrayfire::Backend::CUDA;
const DEVICE: i32 = 0;
fn main() {
arrayfire::set_backend(BACK_END);
arrayfire::set_device(DEVICE);
//Create A matrix
let A_vec:Vec<f64> = vec![1.0, 1.2, 1.1, 0.8, -1.0, 0.0, 0.0, 0.0, -1.2];
let mut A = arrayfire::Array::new(&A_vec, arrayfire::Dim4::new(&[3, 3, 1, 1]));
arrayfire::print_gen("A".to_string(), &A,Some(6));
//A
//1.000000 0.800000 0.000000
//1.200000 -1.000000 0.000000
//1.100000 0.000000 -1.200000
// Set the Linear Matrix Differentail Equation
// dy1/dt = 1.0y1 + 0.8y2 + 0.0y3
// dy2/dt = 1.2y1 + -1.0y2 + 0.0y3
// dy3/dt = 1.1y1 + 0.0y2 + -1.2y3
let diffeq = |t: &arrayfire::Array<f64>, y: &arrayfire::Array<f64>| -> arrayfire::Array<f64> {
arrayfire::matmul(&A, y, arrayfire::MatProp::NONE, arrayfire::MatProp::NONE)
};
//Start at t=0 and end at t=10
//Step size of 0.001
//Relative error of 1E-9
//Absolute error of 1E-9
//Error Type compute the total error of every element in y
let options: RayBNN_DiffEq::ODE::ODE45::ODE45_Options<f64> = RayBNN_DiffEq::ODE::ODE45::ODE45_Options {
tstart: 0.0f64,
tend: 10.0f64,
tstep: 0.001f64,
rtol: 1.0E-9f64,
atol: 1.0E-9f64,
error_select: RayBNN_DiffEq::ODE::ODE45::error_type::TOTAL_ERROR
};
let t_dims = arrayfire::Dim4::new(&[1,1,1,1]);
let mut t = arrayfire::constant::<f64>(0.0,t_dims);
let y0_dims = arrayfire::Dim4::new(&[3,1,1,1]);
let mut y = arrayfire::constant::<f64>(0.0,y0_dims);
let mut dydt = arrayfire::constant::<f64>(0.0,y0_dims);
//Initial Point of Differential Equation
//Set y1(0) = 0.1
//Set y2(0) = 0.2
//Set y3(0) = -0.3
let y0_vec:Vec<f64> = vec![0.1, 0.2, -0.3];
let y0 = arrayfire::Array::new(&y0_vec, y0_dims);
println!("Running");
arrayfire::sync(DEVICE);
let starttime = std::time::Instant::now();
//Run Solver
RayBNN_DiffEq::ODE::ODE45::solve(
&y0
,diffeq
,&options
,&mut t
,&mut y
,&mut dydt
);
arrayfire::sync(DEVICE);
let elapsedtime = starttime.elapsed();
arrayfire::sync(DEVICE);
arrayfire::print_gen("y".to_string(), &y,Some(6));
arrayfire::print_gen("t".to_string(), &t,Some(6));
println!("Computed {} Steps In: {:.6?}", y.dims()[1],elapsedtime);
}
Computed 983 Steps In: 391.827121ms
使用Float 64位精度在CUDA上求解1000x1000矩阵线性常微分方程
//cargo run --example Linear_Matrix_ODE --release
use arrayfire;
use RayBNN_DiffEq;
//Select CUDA and GPU Device 0
const BACK_END: arrayfire::Backend = arrayfire::Backend::CUDA;
const DEVICE: i32 = 0;
fn main() {
arrayfire::set_backend(BACK_END);
arrayfire::set_device(DEVICE);
//Create A matrix from random normal numbers
let A_dims = arrayfire::Dim4::new(&[1000,1000,1,1]);
let A = arrayfire::randn::<f64>(A_dims)/100.0f64;
// Set the Linear Matrix Differentail Equation
// dy/dt = A*y
let diffeq = |t: &arrayfire::Array<f64>, y: &arrayfire::Array<f64>| -> arrayfire::Array<f64> {
arrayfire::matmul(&A, y, arrayfire::MatProp::NONE, arrayfire::MatProp::NONE)
};
//Start at t=0 and end at t=50
//Step size of 0.001
//Relative error of 1E-9
//Absolute error of 1E-9
//Error Type compute the individual error of every element in y
let options: RayBNN_DiffEq::ODE::ODE45::ODE45_Options<f64> = RayBNN_DiffEq::ODE::ODE45::ODE45_Options {
tstart: 0.0f64,
tend: 50.0f64,
tstep: 0.001f64,
rtol: 1.0E-9f64,
atol: 1.0E-9f64,
error_select: RayBNN_DiffEq::ODE::ODE45::error_type::INDIVIDUAL_ERROR
};
let t_dims = arrayfire::Dim4::new(&[1,1,1,1]);
let mut t = arrayfire::constant::<f64>(0.0,t_dims);
let y0_dims = arrayfire::Dim4::new(&[1000,1,1,1]);
let mut y = arrayfire::constant::<f64>(0.0,y0_dims);
let mut dydt = arrayfire::constant::<f64>(0.0,y0_dims);
//Initial Point of Differential Equation
let y0 = arrayfire::randn::<f64>(y0_dims)/100.0f64;
println!("Running");
arrayfire::sync(DEVICE);
let starttime = std::time::Instant::now();
//Run Solver
RayBNN_DiffEq::ODE::ODE45::solve(
&y0
,diffeq
,&options
,&mut t
,&mut y
,&mut dydt
);
arrayfire::sync(DEVICE);
let elapsedtime = starttime.elapsed();
arrayfire::sync(DEVICE);
//let lasty = arrayfire::col(&y, y.dims()[1] as i64);
//arrayfire::print_gen("lasty".to_string(), &lasty,Some(6));
//arrayfire::print_gen("t".to_string(), &t,Some(6));
println!("Computed {} Steps In: {:.6?}", y.dims()[1],elapsedtime);
}
Computed 3366 Steps In: 4.635253s
使用Float 32位精度在CUDA上求解简单线性常微分方程
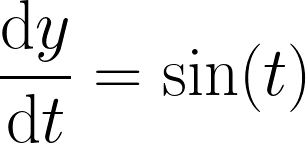
//cargo run --example Linear_ODE_f32 --release
use arrayfire;
use RayBNN_DiffEq;
//Select CUDA and GPU Device 0
const BACK_END: arrayfire::Backend = arrayfire::Backend::CUDA;
const DEVICE: i32 = 0;
fn main() {
arrayfire::set_backend(BACK_END);
arrayfire::set_device(DEVICE);
// Set the Linear Differentail Equation
// dy/dt = sin(t)
let diffeq = |t: &arrayfire::Array<f32>, y: &arrayfire::Array<f32>| -> arrayfire::Array<f32> {
arrayfire::sin(&t)
};
//Start at t=0 and end at t=1000
//Step size of 0.0001
//Relative error of 1E-4
//Absolute error of 1E-4
//Error Type compute the total error of every element in y
let options: RayBNN_DiffEq::ODE::ODE45::ODE45_Options<f32> = RayBNN_DiffEq::ODE::ODE45::ODE45_Options {
tstart: 0.0f32,
tend: 1000.0f32,
tstep: 0.0001f32,
rtol: 1.0E-4f32,
atol: 1.0E-4f32,
error_select: RayBNN_DiffEq::ODE::ODE45::error_type::TOTAL_ERROR
};
let t_dims = arrayfire::Dim4::new(&[1,1,1,1]);
let mut t = arrayfire::constant::<f32>(0.0,t_dims);
let y0_dims = arrayfire::Dim4::new(&[1,1,1,1]);
let mut y = arrayfire::constant::<f32>(0.0,y0_dims);
let mut dydt = arrayfire::constant::<f32>(0.0,y0_dims);
//Initial Point of Differential Equation
//Set y(t=0) = 1.0
let y0 = arrayfire::constant::<f32>(1.0,y0_dims);
println!("Running");
arrayfire::sync(DEVICE);
let starttime = std::time::Instant::now();
//Run Solver
RayBNN_DiffEq::ODE::ODE45::solve(
&y0
,diffeq
,&options
,&mut t
,&mut y
,&mut dydt
);
arrayfire::sync(DEVICE);
let elapsedtime = starttime.elapsed();
arrayfire::sync(DEVICE);
arrayfire::print_gen("y".to_string(), &y,Some(6));
arrayfire::print_gen("t".to_string(), &t,Some(6));
println!("Computed {} Steps In: {:.6?}", y.dims()[1],elapsedtime);
//Error Analysis
let actualy = 2.0f32 - arrayfire::cos(&t);
let error = y - actualy;
//arrayfire::print_gen("error".to_string(), &error,Some(6));
}
Computed 712 Steps In: 450.653767ms
插值求解结果
use arrayfire;
use RayBNN_DataLoader;
use RayBNN_DiffEq;
const BACK_END: arrayfire::Backend = arrayfire::Backend::CUDA;
const DEVICE: i32 = 0;
#[test]
fn test_ODE() {
arrayfire::set_backend(BACK_END);
arrayfire::set_device(DEVICE);
let n:u64 = 10;
let steps:u64 = 10001;
let A_dims = arrayfire::Dim4::new(&[10,10,1,1]);
let mut A = RayBNN_DataLoader::Dataset::CSV::file_to_arrayfire::<f64>(
"./test_data/ODE_A.csv",
);
A = arrayfire::transpose(&A, false);
let D_dims = arrayfire::Dim4::new(&[1,10,1,1]);
let mut D = RayBNN_DataLoader::Dataset::CSV::file_to_arrayfire::<f64>(
"./test_data/ODE_D.csv",
);
D = arrayfire::transpose(&D, false);
let tspan_dims = arrayfire::Dim4::new(&[1,10001,1,1]);
let mut tspan = RayBNN_DataLoader::Dataset::CSV::file_to_arrayfire::<f64>(
"./test_data/ODE_tspan.csv",
);
//tspan = arrayfire::transpose(&tspan, false);
let x0_dims = arrayfire::Dim4::new(&[1,10,1,1]);
let mut x0 = RayBNN_DataLoader::Dataset::CSV::file_to_arrayfire::<f64>(
"./test_data/ODE_x0.csv",
);
x0 = arrayfire::transpose(&x0, false);
let xeval_dims = arrayfire::Dim4::new(&[10001,10,1,1]);
let mut xeval = RayBNN_DataLoader::Dataset::CSV::file_to_arrayfire::<f64>(
"./test_data/ODE_xeval.csv",
);
xeval = arrayfire::transpose(&xeval, false);
let diffeq = |t: &arrayfire::Array<f64>, x: &arrayfire::Array<f64>| -> arrayfire::Array<f64> {
D.clone() + arrayfire::matmul(&A, x, arrayfire::MatProp::NONE, arrayfire::MatProp::NONE)
};
let options: RayBNN_DiffEq::ODE::ODE45::ODE45_Options<f64> = RayBNN_DiffEq::ODE::ODE45::ODE45_Options {
tstart: 0.0,
tend: 100.0,
tstep: 1E-5,
rtol: 1E-15,
atol: 1.0,
error_select: RayBNN_DiffEq::ODE::ODE45::error_type::TOTAL_ERROR
};
let starttime = std::time::Instant::now();
let mut t = arrayfire::constant::<f64>(0.0,A_dims);
let mut f = arrayfire::constant::<f64>(0.0,A_dims);
let mut dfdt = arrayfire::constant::<f64>(0.0,A_dims);
RayBNN_DiffEq::ODE::ODE45::solve(
&x0
,diffeq
,&options
,&mut t
,&mut f
,&mut dfdt
);
let xpred = RayBNN_DiffEq::Interpolate::Linear::run(
&t
,&f
,&dfdt
,&tspan
);
let elapsedtime = starttime.elapsed();
println!("Computed {} Steps In: {:.6?}", xpred.dims()[1], elapsedtime);
let mut relerror = xpred - xeval.clone();
relerror = relerror/xeval;
relerror = arrayfire::abs(&relerror);
let (maxerr,_) = arrayfire::max_all(&relerror);
assert!(maxerr <= 2E-3);
}
在CPU、OpenCL和CUDA之间选择
//Select CPU Device 0
const BACK_END: arrayfire::Backend = arrayfire::Backend::CPU;
const DEVICE: i32 = 0;
//Select OpenCL Device 0
const BACK_END: arrayfire::Backend = arrayfire::Backend::OpenCL;
const DEVICE: i32 = 0;
//Select CUDA Device 0
const BACK_END: arrayfire::Backend = arrayfire::Backend::CUDA;
const DEVICE: i32 = 0;
依赖关系
~7MB
~141K SLoC