Whittaker Smoother

又称 Whittaker-Henderson 或 Whittaker-Eilers 平滑器，是完美的平滑器。它是一种针对等间隔数据的样条平滑的离散时间版本。它最小化以下泛函

$$\sum_{i=0}^n (z_i - y_i)^2 + \lambda \sum_{i=0}^n (\delta ^p z)_i ^2 $$

其中 y 是数据点，z 是平滑函数，$\delta^2 z$ 是 $z_i$ 的 p 阶导数，通过数值方法进行评估。对非平滑函数施加惩罚，$\lambda$ 的值越高，惩罚越重，输出越平滑。

通过求解线性系统 $$x = (W + \lambda * D^T D )^{-1} W y $$ 可以获得平滑输出。其中 W 是权重矩阵（实践中是单位矩阵）和 D 是差分矩阵（参见 difference_matrix 了解其构造）。

示例

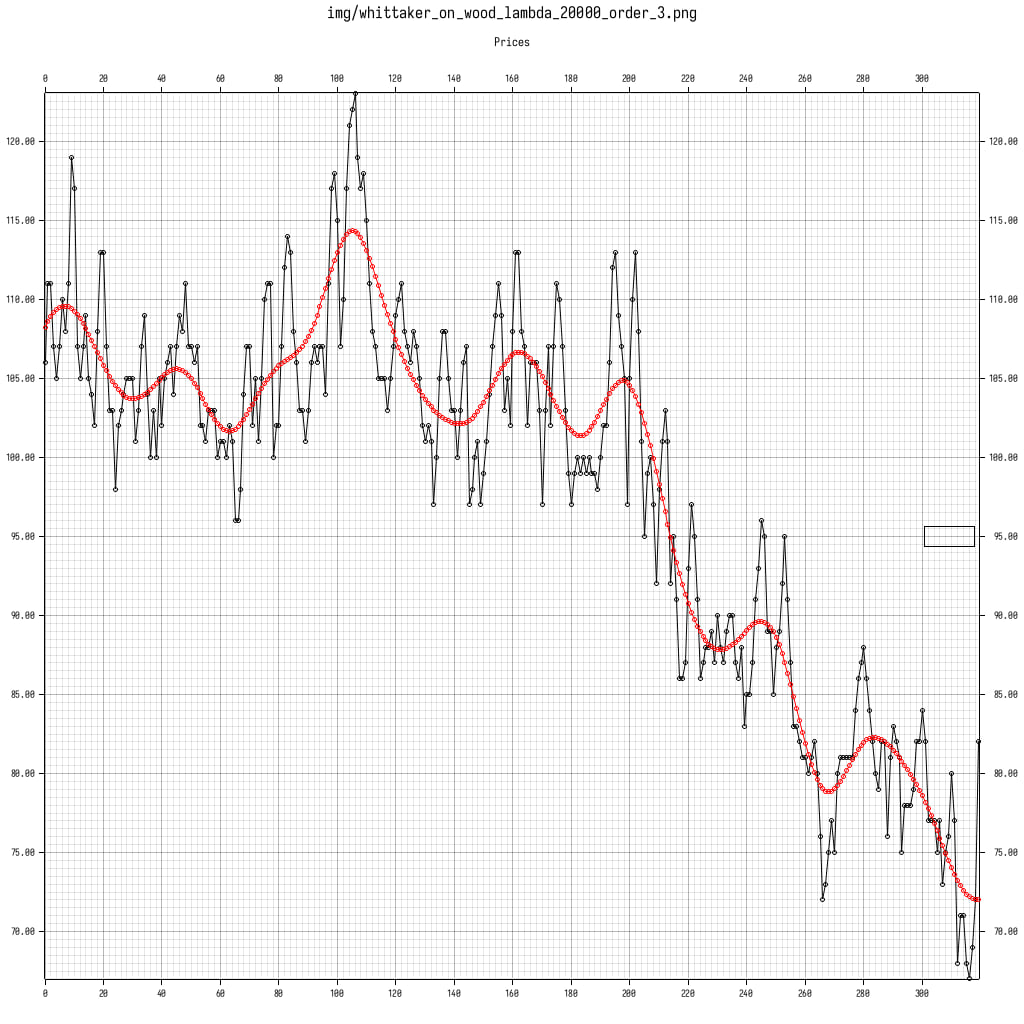
这里我们看到了使用 2 和 3 阶的 wood 数据集进行平滑。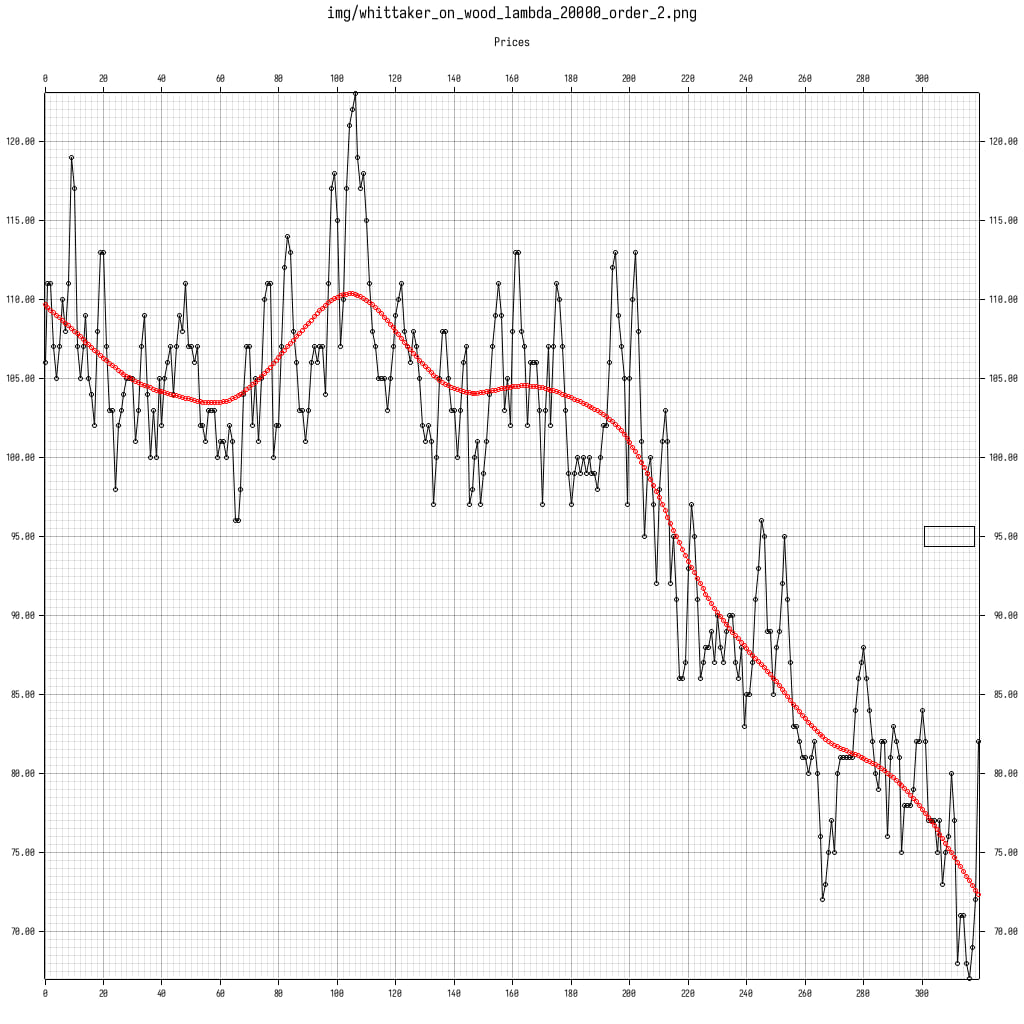

与移动平均和卷积核的比较

与移动平均平滑器相比，这种方法不会受到群延迟的影响。

与 savitzky-golay 滤波器等卷积核相比，边缘值定义良好，无需插值。Savitzky-Golay 滤波器有一个很好的平坦通带，但高频噪声处理不满意，没有足够抑制。当数据导数很重要时，这是一个特别的问题。

用法

要在项目中使用此平滑器，请将以下内容添加到您的 Cargo.toml

[dependencies]
whittaker_smoother = "0.1"

进一步阅读

请参阅 论文 文件夹中的两篇论文，这些论文展示了该方法的更多详细信息。

此实现受到了 一个 Python 实现 的启发。

许可

版权（C）2020 <Mathis Wellmann [email protected]>

本程序是自由软件：您可以按照自由软件基金会发布的GNU Affero通用公共许可证的条款重新分发和/或修改它，无论是许可证的第3版，还是（根据您的选择）任何更新的版本。

本程序的发布是为了希望它是有用的，但没有任何保证；甚至没有关于其商业性或针对特定目的的适用性的暗示性保证。有关更多详细信息，请参阅GNU Affero通用公共许可证。

您应该已经收到随本程序一起提供的GNU Affero通用公共许可证副本。如果没有，请参阅https://www.gnu.org/licenses/。