3个版本 (重大更改)

0.3.0	2023年10月15日
0.2.1	2023年7月30日
0.1.0	2022年2月1日

#835 in 数学

MIT许可证

1.5MB
7.5K SLoC

基于有限元方法的多孔介质模拟器

🚧 进行中...

简介

此代码实现了使用有限元方法对固体、结构和多孔介质行为的模拟器。

请参阅文档以获取更多信息

pmsim文档 - 包含API参考和示例

安装

此crate依赖于russell_lab，因此需要一些外部库。请参阅russell_lab上的所需依赖的安装。

设置Cargo.toml

👆 检查crate版本并相应更新您的Cargo.toml

[dependencies]
gemlab = "*"

示例

对于所有模拟

Legend:
✅ : converged
👍 : converging
🥵 : diverging
😱 : found NaN or Inf
❋  : non-scaled max(R)
?  : no info abut convergence

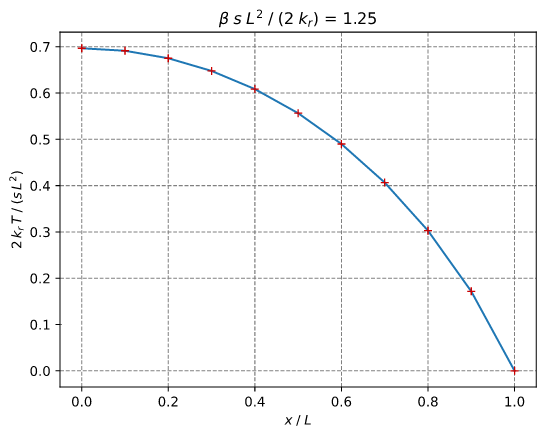
热：Arpaci非线性1d

Arpaci在第130页的示例3-8（变量导热系数）

Arpaci V. S. (1966) 导热传热，Addison-Wesley，551页

测试目标

此测试验证了具有变量导热系数的非线性扩散方程求解器。

网格

Mesh

初始条件

所有点的温度T = 0

边界条件

右侧的x = L处的温度T = 0

配置和参数

稳态模拟
源 = 5
变量导热系数（k = (1 + β T) kᵣ I）其中kᵣ = 2

注意

右侧的温度T = 0（T_inf）必须为零，以便结果为k(T_inf) = kᵣ，这是解析解所要求的。

模拟和结果

heat_arpaci_nonlinear_1d.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    2.50e0❋ 
       .             .             .     2    1.28e0? 
       .             .             .     3   9.36e-2👍
       .             .             .     4   1.25e-3👍
       .             .             .     5   1.42e-7👍
       .             .             .     6  1.35e-14✅

T(0) = 87.08286933869708  (87.08286933869707)

以下图表比较了数值结果与解析结果。

Results

热：Bhatti示例1.5对流

Bhatti在第28页的示例1.5

Bhatti, M.A. (2005) 基本有限元分析和应用，Wiley，700页。

测试目标

此测试验证了具有指定温度和对流的稳态热方程。

网格

Mesh

边界条件

对流 Cc = (27, 20) 在右侧边缘
规定温度 T = 300 在左侧边缘

配置和参数

稳态模拟
无源
恒定导热系数 kx = ky = 1.4

模拟和结果

heat_bhatti_1d5_convection.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    1.05e3❋ 
       .             .             .     2  1.71e-15✅

热：Bhatti 示例 6.22 对流

第 449 页 Bhatti 的示例 6.22

Bhatti, M.A. (2005) 基本有限元分析和应用，Wiley，700页。

测试目标

此测试验证了规定温度、对流、通量和体积源项的稳态热方程。此外，它还检查了 Qua8 元素的使用。

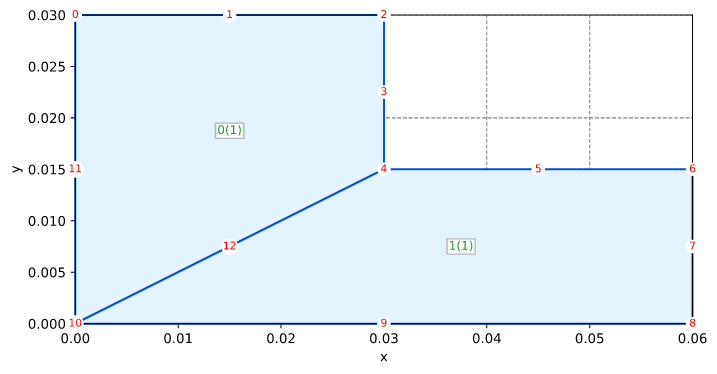
网格

Mesh

边界条件（见第 445 页）

通量 Qt = 8,000 在左侧边缘，边 (0,10,11)
对流 Cc = (55, 20) 在顶部边缘（0,2,1）、（2,4,3）和（4,6,5）
规定温度 T = 110 在底部边缘（8,10,9）

配置和参数

稳态模拟
源 = 5e6 在该区域内
恒定导热系数 kx = ky = 45

模拟和结果

heat_bhatti_6d22_convection.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    3.09e4❋ 
       .             .             .     2  6.09e-16✅

热：Lewis 示例 6.4.2 瞬态 1d

第 159 页 Lewis 的示例 6.4.2

Lewis R, Nithiarasu P, 和 Seetharamu KN（2004）有限元法在热和流体流动中的应用基础，Wiley，341页

测试目标

此测试验证了 1D 中的瞬态扩散

网格

o-----------------------------------------------------------o
|    |    |    |    |    |    |    |    |    |    .....     | h = 1
o-----------------------------------------------------------o
                     <-  L = 20 ->

Mesh

初始条件

所有点的温度T = 0

边界条件

通量 Qt = 1 在 x = 0 的左侧

配置和参数

瞬态模拟
无源
恒定导热系数 kx = ky = 1
系数 ρ = 1

模拟和结果

heat_lewis_transient_1d.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1   6.67e-1❋ 
       .             .             .     2  2.36e-16✅
       2   2.000000e-1   1.000000e-1     .        .  
       .             .             .     1    1.24e0❋ 
       .             .             .     2  6.07e-16✅
       3   3.000000e-1   1.000000e-1     .        .  
       .             .             .     1    1.08e0❋ 
       .             .             .     2  2.55e-16✅
       4   4.000000e-1   1.000000e-1     .        .  
       .             .             .     1   9.73e-1❋ 
       .             .             .     2  3.38e-16✅
       5   5.000000e-1   1.000000e-1     .        .  
       .             .             .     1   8.94e-1❋ 
       .             .             .     2  3.25e-16✅
       6   6.000000e-1   1.000000e-1     .        .  
       .             .             .     1   8.33e-1❋ 
       .             .             .     2  4.24e-16✅
       7   7.000000e-1   1.000000e-1     .        .  
       .             .             .     1   7.84e-1❋ 
       .             .             .     2  6.89e-16✅
       8   8.000000e-1   1.000000e-1     .        .  
       .             .             .     1   7.44e-1❋ 
       .             .             .     2  4.46e-16✅
       9   9.000000e-1   1.000000e-1     .        .  
       .             .             .     1   7.09e-1❋ 
       .             .             .     2  5.85e-16✅
      10    1.000000e0   1.000000e-1     .        .  
       .             .             .     1   6.79e-1❋ 
       .             .             .     2  1.03e-15✅

point = 0, x = 0.00, T = 1.105099, diff = 2.3280e-2
point = 3, x = 0.00, T = 1.105099, diff = 2.3280e-2
point = 7, x = 0.00, T = 1.105099, diff = 2.3280e-2
point = 4, x = 1.00, T = 0.376835, diff = 2.2447e-2
point = 6, x = 1.00, T = 0.376835, diff = 2.2447e-2
point = 1, x = 2.00, T = 0.085042, diff = 1.5467e-2
point = 2, x = 2.00, T = 0.085042, diff = 1.5467e-2

热：Mathematica 轴对称 Nafems

来自 Mathematica 热传递模型验证测试（HeatTransfer-FEM-Stationary-2DAxisym-Single-HeatTransfer-0002）

NAFEMS 基准测试

https://reference.wolfram.com/language/PDEModels/tutorial/HeatTransfer/HeatTransferVerificationTests.html

测试目标

此测试验证了具有局部通量边界条件的稳态热方程

MESH (not-to-scale, not-equal-axis)

0.14     ||++++++++++++++++++++++++
         ||   |    |    |    |    +
         ||-----------------------+
         ||   |    |    |    |    +
0.10  →→ |------------------------+  yb
      →→ |    |    |    |    |    +
      →→ |------------------------+
      →→ |    |    |    |    |    +
      →→ |------------------------+
      →→ |    |    |    |    |    +
0.04  →→ |--------(#)-------------+  ya
         ||   |    |    |    |    +
         ||-----------------------+
         ||   |    |    |    |    +
0.00     ||++++++++++++++++++++++++
        0.02     0.04            0.10
        rin      rref            rout

'+' indicates sides with T = 273.15
|| means insulated
→→ means flux with Qt = 5e5
(#) indicates a reference point to check the results

Mesh

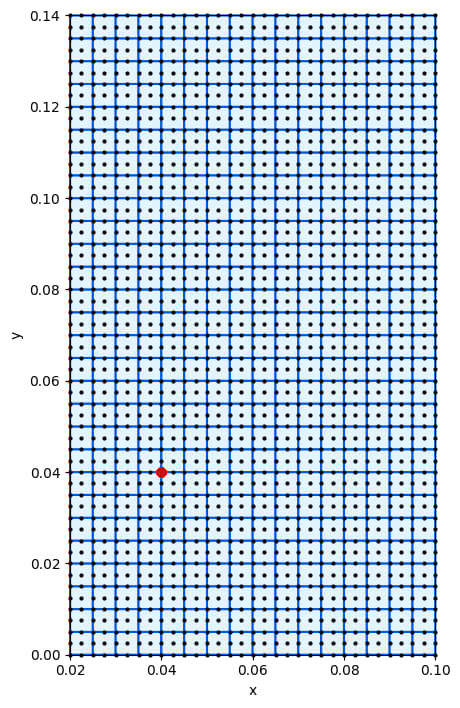
初始条件

所有点的温度T = 0

边界条件

温度 T = 273.15 在顶部、底部和右侧边缘
通量 Qt = 5e5 在中间左侧边缘（y=0.04 到 y=0.10）

配置和参数

稳态模拟
无源
恒定导热系数 kx = ky = 52

模拟和结果

heat_mathematica_axisym_nafems.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    4.45e3❋ 
       .             .             .     2  3.23e-12✅

T = 332.9704335048643, reference = 332.97, rel_error = 0.00013019 %

热：Mathematica 轴对称简单

来自 Mathematica 热传递模型验证测试（HeatTransfer-FEM-Stationary-2DAxisym-Single-HeatTransfer-0001）

2D 轴对称单方程

https://reference.wolfram.com/language/PDEModels/tutorial/HeatTransfer/HeatTransferVerificationTests.html

测试目标

此测试验证了具有规定通量的 1D 中稳态热方程

网格

  →→ ---------------------
  →→ |    |    |    |    |  h
  →→ ---------------------
    1.0                 2.0
    rin                rout

Mesh

初始条件

所有点的温度T = 0

边界条件

温度 T = 10.0 在右侧边缘
通量 Qt = 100.0 在左侧边缘

配置和参数

稳态模拟
无源
恒定导热系数 kx = ky = 10.0

模拟和结果

heat_mathematica_axisym_simple.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    3.51e2❋ 
       .             .             .     2  3.55e-13✅

杆：Bhatti 示例 1.4 拉杆

第 25 页 Bhatti 的示例 1.4

Bhatti, M.A. (2005) 基本有限元分析和应用，Wiley，700页。

测试目标

此测试验证了一个带有杆单元和集中力的 2D 框架

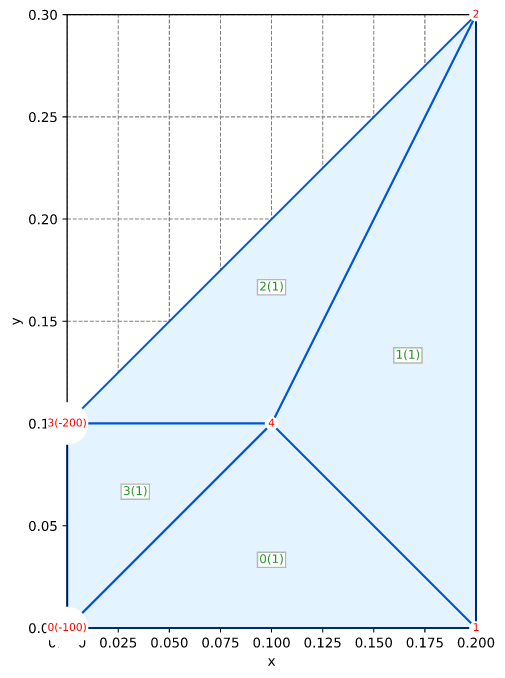
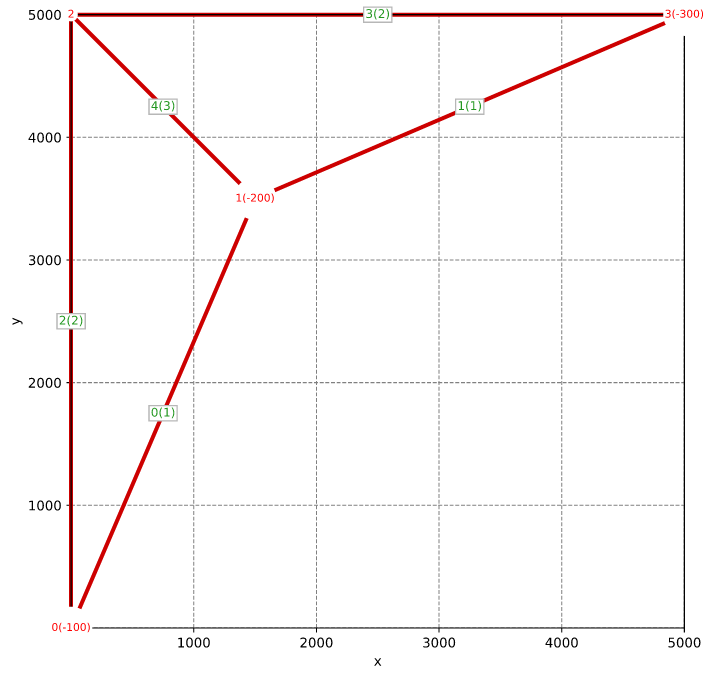
网格

Mesh

边界条件

在点 0 和 3 处完全固定
在点 1 上有集中载荷，Fy = -150,000

配置和参数

静态模拟
属性 1：面积 = 4,000；杨氏模量 = 200,000
属性 2：面积 = 3,000；杨氏模量 = 200,000
属性 3：面积 = 2,000；杨氏模量 = 70,000

模拟和结果

rod_bhatti_1d4_truss.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    1.50e5❋ 
       .             .             .     2  1.46e-11✅

固体 Bhatti 示例 1.6 平面应力

第 32 页 Bhatti 的示例 1.6

Bhatti, M.A. (2005) 基本有限元分析和应用，Wiley，700页。

测试目标

此测试验证了一个通过假设平面应力建模的薄梁模型的平衡

网格

Mesh

边界条件

在点 0 和 1 处完全固定
在边缘（1,3）和（3,5）上沿分布载荷 Qn = -20

配置和参数

静态模拟
杨氏模量 = 10,000
泊松比 = 0.2
平面应力，厚度 = 0.25

模拟和结果

solid_bhatti_1d6_plane_stress.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    1.00e1❋ 
       .             .             .     2  3.91e-14✅

固体 Felippa 厚圆柱轴对称

第 14-3 页 Felippa 的基准 14.1（图 14.1）

Felippa C，高级有限元法

测试目标

此测试验证了内部压力下鸡圆柱管轴对称建模。存在一个解析解，是为平面应变情况开发的。然而，此测试采用轴对称表示。

网格

            Uy FIXED
 →o------o------o------o------o
 →|      |   .......   |      |
 →o------o------o------o------o
            Uy FIXED

边界条件

垂直固定底部边缘
垂直固定顶部边缘
在左侧边缘施加分布载荷 Qn = -PRESSURE

配置和参数

静态模拟
杨氏模量 = 1000，泊松比 = 0.0
轴对称
注意：使用 4 个积分点，因为它与 Qua8 一起给出更好的结果

模拟和结果

solid_felippa_thick_cylinder_axisym.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    5.33e1❋ 
       .             .             .     2  3.16e-13✅

point = 0, r = 4.0, Ux = 0.055238095238095454, diff = 2.1510571102112408e-16
point = 1, r = 7.0, Ux = 0.040544217687075015, diff = 1.8735013540549517e-16
point = 4, r = 5.5, Ux = 0.04510822510822529, diff = 1.8041124150158794e-16
point = 8, r = 10.0, Ux = 0.03809523809523828, diff = 1.8041124150158794e-16
point = 10, r = 8.5, Ux = 0.03859943977591054, diff = 1.8041124150158794e-16

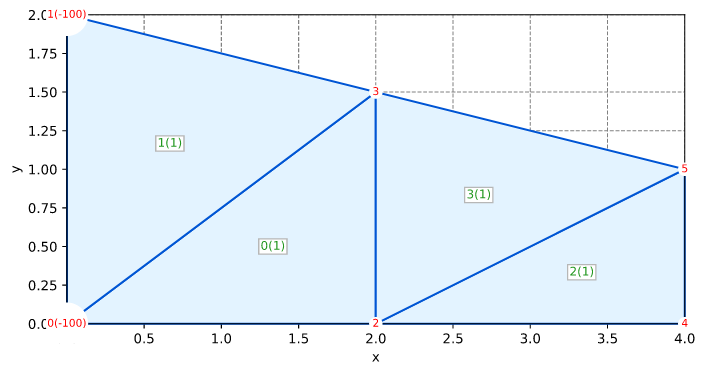
固体 Smith 图 5.2 三角3 平面应力

第 173 页 Smith 的示例 5.2（图 5.2）

Smith IM，Griffiths DV，和 Margetts L（2014）有限元法编程，Wiley，第五版，664页

测试目标

此测试验证了使用 Tri3 元素的平面应变模拟

网格

              1.0 kN/m²
        ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
 0.0   ▷0---------1---------2
        |       ,'|       ,'|   E = 1e6 kN/m²
        |  0  ,'  |  2  ,'  |   ν = 0.3
        |   ,'    |   ,'    |
        | ,'   1  | ,'  3   |   connectivity:
-0.5   ▷3'--------4'--------5     0 : 1 0 3
        |       ,'|       ,'|     1 : 3 4 1
        |  4  ,'  |  6  ,'  |     2 : 2 1 4
        |   ,'    |   ,'    |     3 : 4 5 2
        | ,'   5  | ,'   7  |     4 : 4 3 6
-1.0   ▷6'--------7'--------8     5 : 6 7 4
        △         △         △     6 : 5 4 7
                                  7 : 7 8 5
       0.0       0.5       1.0

Mesh

边界条件

水平固定左侧边缘
垂直固定底部边缘
顶部边缘分布载荷Qn = -1.0

配置和参数

静态模拟
E = 1e6
Poisson = 0.3
平面应变

模拟和结果

solid_smith_5d2_tri3_plane_strain.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1   5.00e-1❋ 
       .             .             .     2  5.55e-16✅

固体Smith图5.7 Tri15平面应变

Smith的例子5.7（图5.7）在第178页

Smith IM，Griffiths DV，和 Margetts L（2014）有限元法编程，Wiley，第五版，664页

测试目标

本测试验证了使用Tri15单元的平面应变模拟

MESH
        1.0 kN/m²
         ↓↓↓↓↓↓
 0.0  Ux o----o---------------o Ux
      F  |   /|           _.-'| F
      I  |  / |       _.-'    | I    15-node
      X  | /  |   _.-'        | X    triangles
      E  |/   |.-'            | E
-2.0  D  o----o---------------o D
        0.0  1.0             6.0
            Ux and Uy FIXED

Mesh

边界条件

水平固定左侧边缘
水平固定右边缘
水平垂直固定底边缘
点0、5、10、15、20的集中载荷（Fy）分别等于-0.0778、-0.3556、-0.1333、-0.3556、-0.0778

注意：分布载荷通过集中力直接建模，以便我们可以将数值结果与书中的结果进行比较。

配置和参数

静态模拟
E = 1e5
泊松比 = 0.2
平面应变

注意：书中图中的Poisson系数与代码中的系数不同。书中图5.8给出的结果对应于代码中的系数（Poisson = 0.2）

模拟和结果

solid_smith_5d7_tri15_plane_strain.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1   3.56e-1❋ 
       .             .             .     2  2.16e-15✅

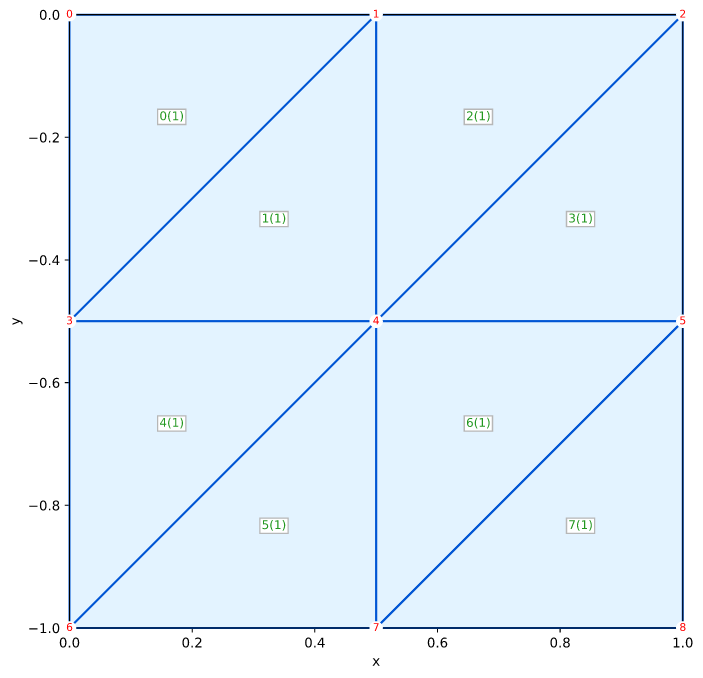
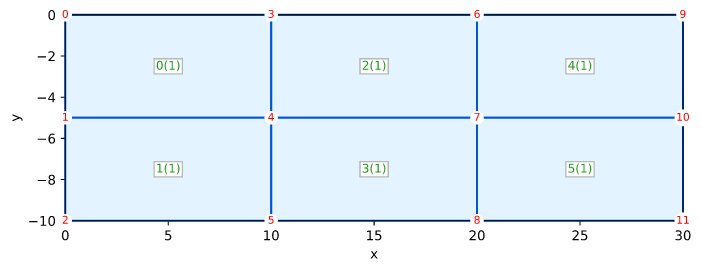
固体Smith图5.11 Qua4平面应变Uy

Smith的例子5.11（图5.11）在第180页

Smith IM，Griffiths DV，和 Margetts L（2014）有限元法编程，Wiley，第五版，664页

测试目标

本测试验证了指定位移的平面应变模拟

网格

       Uy DISPLACEMENT
 0.0      0----------3----------6----------9
       Ux |          |          |          | Ux
       F  |          |          |          | F
       I  1----------4----------7---------10 I
       X  |          |          |          | X
       E  |          |          |          | E
-10.0  D  2----------5----------8---------11 D
         0.0       10.0       20.0       30.0
                    Ux and Uy FIXED

Mesh

边界条件

水平固定左侧边缘
水平固定右边缘
水平垂直固定底边缘
在x ≤ 10的顶部边缘指定位移Uy = -1e-5

配置和参数

静态模拟
E = 1e6
Poisson = 0.3
平面应变

模拟和结果

solid_smith_5d11_qua4_plane_strain_uy.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    2.21e1❋ 
       .             .             .     2  4.50e-16✅

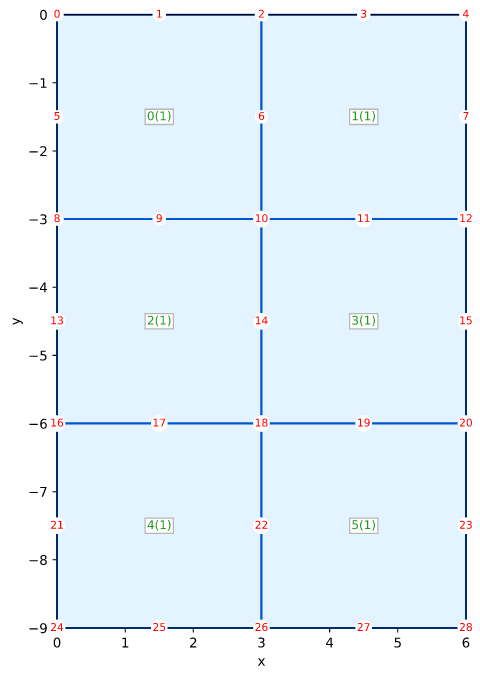
固体Smith图5.15 Qua8平面应变

Smith的例子5.15（图5.15）在第183页

Smith IM，Griffiths DV，和 Margetts L（2014）有限元法编程，Wiley，第五版，664页

测试目标

本测试验证了使用Qua8单元和降阶积分的平面应变模拟

网格

         1.0 kN/m²
        ↓↓↓↓↓↓↓↓↓↓↓
 0.0    0----1----2----3----4
        |         |         |
        5         6         7
        |         |         |
-3.0 Ux 8----9---10---11---12 Ux
     F  |         |         | F
     I 13        14        15 I
     X  |         |         | X
-6.0 E 16---17---18---19---20 E
     D  |         |         | D
       21        22        23
        |         |         |
-9.0   24---25---26---27---28
       0.0       3.0       6.0
           Ux and Uy FIXED

Mesh

边界条件

水平固定左侧边缘
水平固定右边缘
水平垂直固定底边缘
顶部边缘（x ≤ 3）分布载荷Qn = -1

配置和参数

静态模拟
E = 1e6
Poisson = 0.3
平面应变
注意：使用4个点的降阶积分

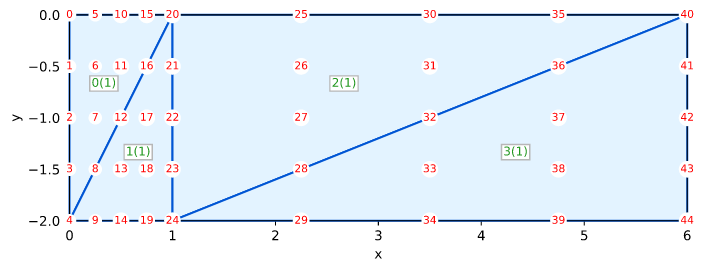
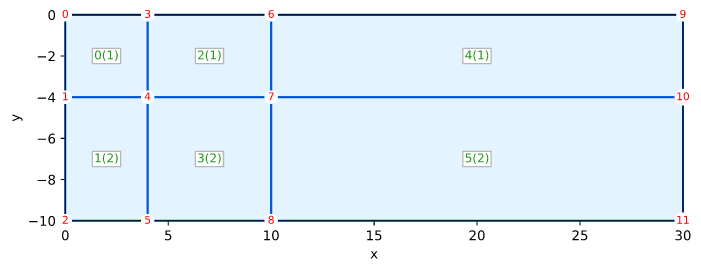
固体Smith图5.17 Qua4轴对称

Smith的例子5.17（图5.17）在第187页

Smith IM，Griffiths DV，和 Margetts L（2014）有限元法编程，Wiley，第五版，664页

测试目标

本测试验证了轴对称平衡问题

网格

              1.0 kN/m²
         ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
  0.0    0------3----------6-------------------9
      Ux | (0)  |   (2)    |        (4)        | Ux
      F  | [1]  |   [1]    |        [1]        | F
 -4.0 I  1------4----------7------------------10 I
      X  | (1)  |   (3)    |        (5)        | X
      E  | [2]  |   [2]    |        [2]        | E
-10.0 D  2------5----------8------------------11 D
        0.0    4.0       10.0                30.0
                     Ux and Uy FIXED

Mesh

边界条件

水平固定左侧边缘
水平固定右边缘
水平垂直固定底边缘
点0、3、6的集中载荷（Fy）分别等于
-2.6667、-23.3333、-24.0
顶部边缘（x ≤ 4）分布载荷Qn = -1

配置和参数

静态模拟
上层：E = 100，Poisson = 0.3
下层：E = 1000，Poisson = 0.45
平面应变
注意：使用9个积分点

模拟和结果

solid_smith_5d15_qua8_plane_strain.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    2.00e0❋ 
       .             .             .     2  7.16e-15✅

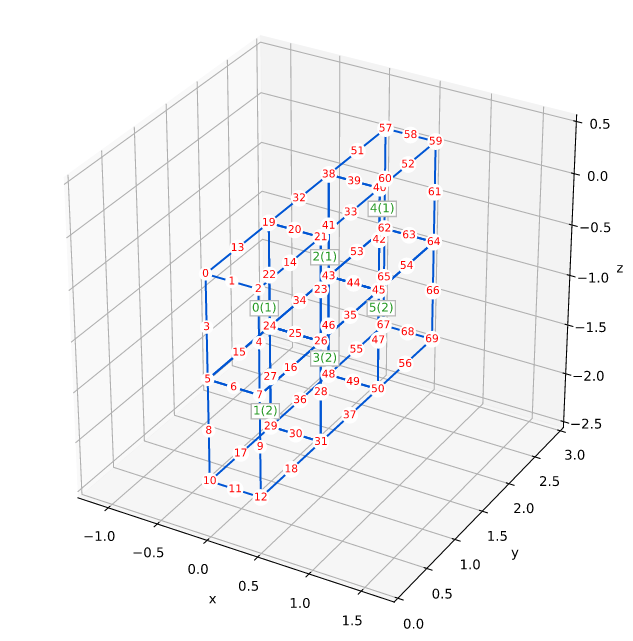
固体Smith图5.24 Hex20 3D

Smith的例子5.24（图5.24）在第195页

Smith IM，Griffiths DV，和 Margetts L（2014）有限元法编程，Wiley，第五版，664页

测试目标

本测试验证了使用Hex20的3D模拟

网格

Mesh

边界条件

水平固定“背面”上x=0的垂直边界面与x垂直
水平固定“左侧”上y=0的垂直边界面与y垂直
将所有Ux、Uy、Uz设置为0，对于“底部”上z=0的垂直边界面与z垂直
在顶部面上y ≤ 1的部分施加分布载荷Qn = -1
注意：“前面”和“右侧”面（x>0或y>0）没有固定。

配置和参数

上层：E = 100，Poisson = 0.3
下层：E = 50，Poisson = 0.3
使用8个点的降阶积分

模拟和结果

solid_smith_5d24_hex20_3d.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1   1.67e-1❋ 
       .             .             .     2  4.73e-16✅

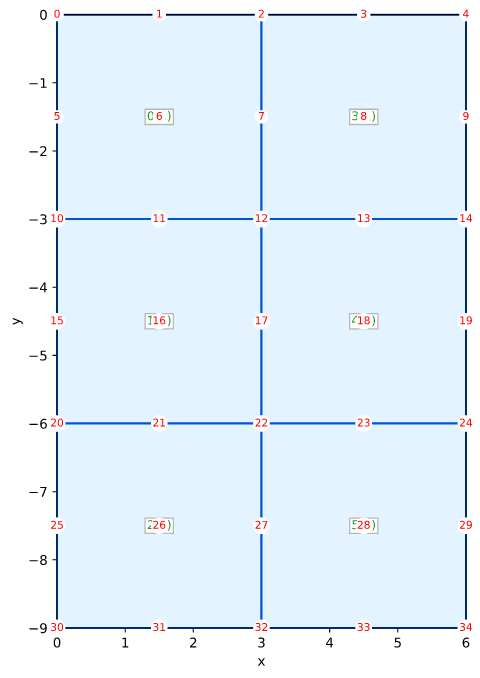
固体Smith图5.27 Qua9平面应变

Smith的例子5.27（图5.27）在第200页

Smith IM，Griffiths DV，和 Margetts L（2014）有限元法编程，Wiley，第五版，664页

测试目标

本测试验证了使用Qua9单元和全积分的平面应变模拟。注意：本例与例子5.15类似，区别在于使用了Qua9单元。

网格

          1.0 kN/m²
         ↓↓↓↓↓↓↓↓↓↓↓
 0.0     0----1----2----3----4
         |         |         |
         5    6    7    8    9
         |         |         |
-3.0 Ux 10---11---12---13---14 Ux
     F   |         |         | F
     I  15   16   17   18   19 I
     X   |         |         | X
-6.0 E  20---21---22---23---24 E
     D   |         |         | D
        25   26   27   28   29
         |         |         |
-9.0    30---31---32---33---34
        0.0       3.0       6.0
            Ux and Uy FIXED

Mesh

边界条件

水平固定左侧边缘
水平固定右边缘
水平垂直固定底边缘
顶部边缘（x ≤ 3）分布载荷Qn = -1

配置和参数

静态模拟
E = 1e6
Poisson = 0.3
平面应变

模拟和结果

solid_smith_5d27_qua9_plane_strain.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1    2.00e0❋ 
       .             .             .     2  5.66e-15✅

固体Smith图5.30 Tet4 3D

Smith的例子5.30（图5.30）在第202页

Smith IM，Griffiths DV，和 Margetts L（2014）有限元法编程，Wiley，第五版，664页

测试目标

本测试验证了使用Tet4的3D模拟

网格

Mesh

边界条件

水平固定“背面”上x=0的垂直边界面与x垂直
水平固定“左侧”上y=0的垂直边界面与y垂直
垂直固定“底部”上z=0的垂直边界面与z垂直
对顶部节点施加垂直（Fz）集中载荷
Fz @ 0和5 = -0.1667，Fz @ 1和4 = -0.3333
（不要使用更多的小数位数，如代码中所示，以便我们可以与书中的结果进行比较）

配置和参数

E = 100，Poisson = 0.3

模拟和结果

solid_smith_5d30_tet4_3d.rs

                                                  _   
timestep             t            Δt  iter    max(R)  
       1   1.000000e-1   1.000000e-1     .        .  
       .             .             .     1   3.33e-1❋ 
       .             .             .     2  9.30e-17✅

依赖项

~18–29MB
~426K SLoC

3个版本 (重大更改)

基于有限元方法的多孔介质模拟器

目录

简介

安装

设置Cargo.toml

示例

热：Arpaci非线性1d

测试目标

网格

初始条件

边界条件

配置和参数

注意

模拟和结果

热：Bhatti示例1.5对流

测试目标

网格

边界条件

配置和参数

模拟和结果

热：Bhatti 示例 6.22 对流

测试目标

网格

边界条件（见第 445 页）

配置和参数

模拟和结果

热：Lewis 示例 6.4.2 瞬态 1d

测试目标

网格

初始条件

边界条件

配置和参数

模拟和结果

热：Mathematica 轴对称 Nafems

测试目标

初始条件

边界条件

配置和参数

模拟和结果

热：Mathematica 轴对称简单

测试目标

网格

初始条件

边界条件

配置和参数

模拟和结果

杆：Bhatti 示例 1.4 拉杆

测试目标

网格

边界条件

配置和参数

模拟和结果

固体 Bhatti 示例 1.6 平面应力

测试目标

网格

边界条件

配置和参数

模拟和结果

固体 Felippa 厚圆柱轴对称

测试目标

网格

边界条件

配置和参数

模拟和结果

固体 Smith 图 5.2 三角3 平面应力

测试目标

网格

边界条件

配置和参数

模拟和结果

固体Smith图5.7 Tri15平面应变

测试目标

边界条件

配置和参数

模拟和结果

固体Smith图5.11 Qua4平面应变Uy

测试目标

网格

边界条件