5个版本
| 0.2.3 | 2023年10月31日 |
|---|---|
| 0.2.2 | 2023年5月11日 |
| 0.2.1 | 2023年4月17日 |
| 0.2.0 | 2023年3月27日 |
| 0.1.0 | 2023年3月13日 |
#361 in 算法
用于 mot-rs
190KB
321 行
用于目标跟踪的离散卡尔曼滤波器实现
卡尔曼滤波器通过考虑系统在时间k的状态是由时间k-1的状态演变而来,通过线性随机差分方程估计系统在时间k的状态。请参阅参考https://en.wikipedia.org/wiki/Kalman_filter
换句话说,卡尔曼滤波器的作用是通过使用当前状态的前置知识来预测下一个状态。
在这个仓库中,考虑到连续时间模型和离散时间测量,实现了混合卡尔曼滤波器。请参阅参考https://en.wikipedia.org/wiki/Kalman_filter#Hybrid_Kalman_filter
目录
主要算法和方程
定义所提到的 线性随机差分方程
$$\chi_{k} = A⋅\chi_{k-1} + B⋅u_{k-1} + w_{k-1} \tag{1}$$
定义测量模型:$$z_{k} = H⋅\chi_{k} + v_{k}\tag{2}$$
让我们定义变量
- $A$ (有时写成 $F$,但我更喜欢用 $A$) - 大小为 $n \times n$ 的 状态转换矩阵,它将状态 $k-1$ 与状态 $k$ 相关联
- $B$ - 大小为 $n \times l$ 的控制输入矩阵,它应用于 可选 控制输入 $u_{k-1}$
- $H$ - 大小为 $m \times n$ 的转换(观测)矩阵。
- $u_{k}$ - 控制输入
- $w_{k}$ - 带协方差 $Q$ 的过程噪声向量。高斯噪声,具有正态概率分布:$$w(t) \sim N(0, Q) \tag{3}$$
- $v_{k}$ - 带协方差 $R$ 的测量噪声向量(不确定性)。高斯噪声,具有正态概率分布:$$v(t) \sim N(0, R) \tag{4}$$
预测
让我们使用破折号“ - ”作为上标来表示先验状态。
矩阵表示中的先验状态定义为
$$\hat{\chi}^-_ {k} = A⋅\hat{\chi}_ {k-1} + B⋅u_ {k-1} \tag{5}$$
$$,其中 $\hat{\chi}^-_ {k}$ - 先验状态(也称为预测),$\hat{\chi}_ {k-1}$ - 后验状态(也称为上一个)$$
注意:0时刻(初始)的后验状态 $\hat{\chi}_{k-1}$ 应该被 猜测
误差协方差矩阵 $P^-$ 定义为
$$P^-_{k} = A⋅P_{k-1}⋅A^{T} + Q \tag{6}$$
$$\text{,其中 $P_{k-1}$ - 上一次估计的误差协方差矩阵,大小为 $n \times n$(应与转换矩阵维度相匹配),}$$ $$\text{Q - 过程噪声协方差}$$
注意: $P_{k-1}$ 在0时刻(初始)应该被 猜测
校正
卡尔曼增益(最小化估计方差)在矩阵表示法中定义为
$$K_{k} = P^-_{k}⋅H^{T}⋅(H⋅P^-_{k}⋅H^{T}+R)^{-1} \tag{7}$$
$$\text{,其中 H - 转换矩阵,R - 测量噪声协方差}$$
在评估卡尔曼增益后,我们需要更新先验状态 $\hat{\chi}^-_{k}$。为了做到这一点,我们需要计算测量残差
$$r_{k} = z_{k} - H⋅\hat{\chi}^-_{k} \tag{8}$$
$$\text{,其中 $z_{k}$ - 真实测量,$H⋅\hat{\chi}^-_{k}$ - 上一次估计的测量}$$
然后我们可以更新预测状态 $\hat{\chi}_{k}$
$$\hat{\chi}_{k} = \hat{\chi}^-_{k} + K_{k}⋅r_{k}$$
$$\text{或} \tag{9}$$
$$\hat{\chi}_{k} = \hat{\chi}^-_{k} + K_{k}⋅(z_{k} - H⋅\hat{\chi}^-_{k})$$
之后,我们应该更新误差协方差矩阵 $P_{k}$,它将在下一个时间步(以此类推)中使用:$$P_{k} = (I - K_{k}⋅H)⋅P^-_{k}\tag{10}$$ $$\text{,其中 $I$ - 单位矩阵(主对角线上的元素为1,其余元素为0的方阵)}$$
总体来说
整个算法可以用高级图来描述
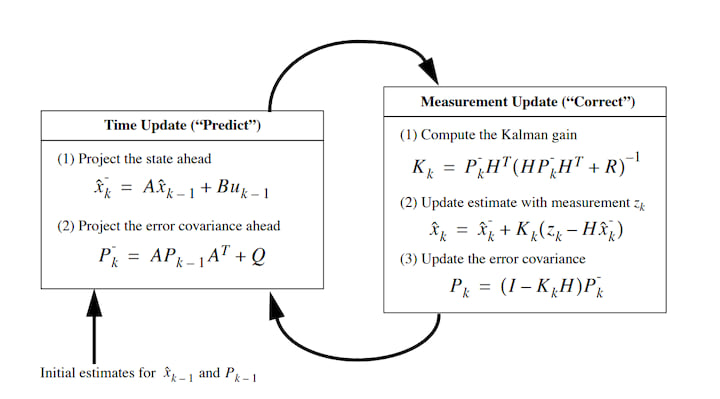
图1. 卡尔曼滤波器的工作原理。Welch & Bishop,《卡尔曼滤波简介》
一维卡尔曼滤波器
考虑加速度运动,让我们写下它的方程
速度:$$v = v_{0} + at \tag{11}$$ $$v(t) = x'(t) $$ $$a(t) = v'(t) = x''(t)$$
位置:$$x = x_{0} + v_{0}t + \frac{at^2}{2} \tag{12}$$
让我们将 $(11)$ 和 $(12)$ 写成拉格朗日形式
$$x'_{k} = x'_{k-1} + x''_{k-1}\Delta t \tag{13}$$
$$x_{k} = x_{k-1} + x'_{k-1}\Delta t + \frac{x''_{k-1}(\Delta t^2)}{2} \tag{14}$$
状态向量 $\chi_{k}$ 看起来像
$$\chi_{k} = \begin{bmatrix} x_{k} \ x'_{k} \end{bmatrix} = \begin{bmatrix} x_{k-1} + x'_{k-1}\Delta t + \frac{x''_{k-1}(\Delta t^2)}{2} \ x'_{k-1} + x''_{k-1}\Delta t \end{bmatrix} \tag{15}$$
状态向量 $\chi_{k}$ 的矩阵形式
$$\chi_{k} = \begin{bmatrix} x_{k} \ x'_{k} \end{bmatrix} = \begin{bmatrix} 1 & \Delta t \ 0 & 1 \end{bmatrix} ⋅ \begin{bmatrix} x_{k-1} \ x'_{k-1} \end{bmatrix} + \begin{bmatrix} \frac{\Delta t^2}{2} \ \Delta t \end{bmatrix} ⋅ x''_{k-1} = \begin{bmatrix} 1 & \Delta t \ 0 & 1 \end{bmatrix} ⋅ \chi_{k-1} + \begin{bmatrix} \frac{\Delta t^2}{2} \ \Delta t \end{bmatrix} ⋅ x''_{k-1} \tag{16}$$
仔细观察 $(16)$ 和 $(1)$,我们可以将转换矩阵 $A$ 和控制输入矩阵 $B$ 写成以下形式
$$A = \begin{bmatrix} 1 & \Delta t \ 0 & 1 \end{bmatrix} \tag{17}$$
$$B = \begin{bmatrix} \frac{\Delta t^2}{2} \ \Delta t \end{bmatrix} \tag{18}$$
让我们找到转换矩阵 $H$。根据 $(2)$
$$z_{k} = H⋅\chi_{k} + v_{k} = \begin{bmatrix} 1 & 0 \end{bmatrix} ⋅\begin{bmatrix} x_{k} \ {x'_{k}} \end{bmatrix} + v_{k} \tag{19}$$
$$H = \begin{bmatrix} 1 & 0 \end{bmatrix} \tag{20}$$
注意: $(19)$ 中的 $v_{k}$ 不是速度,而是测量噪声!不要与符号混淆。例如:
$$\text{ $ \chi_{k} = \begin{bmatrix} 375.74 \ 0 - \text{假设速度为零} \end{bmatrix} $,$ v_{k} = 2.64 => $}$$
$$\text{ $=> z_{k} = \begin{bmatrix} 1 & 0 \end{bmatrix} ⋅\begin{bmatrix} 375.74 \ 0 \end{bmatrix} + 2.64 = \begin{bmatrix} 378.38 & 2.64 \end{bmatrix} $ - 您可以看到,第一个向量参数只是噪声 $v_{k}$ 添加到观测 $x_{k}$ 上,第二个参数是噪声 $v_{k}$ 本身。}$$
$$\text{到观测 $x_{k}$ 和第二个参数是噪声 $v_{k}$ 本身。}$$
过程噪声协方差矩阵 $Q$
$$Q = \begin{matrix} & \begin{matrix}x && x'\end{matrix} \ \begin{matrix}x \ x'\end{matrix} & \begin{bmatrix} \sigma^2_{x} & \sigma_{x} \sigma_{x'} \ \sigma_{x'} \sigma_{x} & \sigma^2_{x'}\end{bmatrix} \\ \end{matrix} \tag{21}$$
$$\text{,其中} $$
$$ \text{$\sigma_{x}$ - 位置的标准偏差} $$
$$ \text{$\sigma_{x'}$ - 速度的标准偏差} $$
由于我们知道$(14)$,我们可以定义$\sigma_{x}$和$\sigma_{x'}$为
$$ \sigma_{x} = \sigma_{x''} \frac{\Delta t^2}{2} \tag{22}$$
$$ \sigma_{x'} = \sigma_{x''} \Delta t \tag{23}$$
$$\text{,其中 $\sigma_{x''}$ - 加速度的标准偏差(调整值)} $$
现在,过程噪声协方差矩阵$Q$可以定义为
$$ Q = \begin{bmatrix} (\sigma_{x''} \frac{\Delta t^2}{2})^2 & \sigma_{x''} \frac{\Delta t^2}{2} \sigma_{x''} \Delta t \ \sigma_{x''} \Delta t \sigma_{x''} \frac{\Delta t^2}{2} & (\sigma_{x''} \Delta t)^2 \end{bmatrix} = $$
$$ = \begin{bmatrix} (\sigma_{x''} \frac{\Delta t^2}{2})^2 & (\sigma_{x''})^2 \frac{\Delta t^2}{2} \Delta t \ (\sigma_{x''})^2 \Delta t \frac{\Delta t^2}{2} & (\sigma_{x''} \Delta t)^2 \end{bmatrix} = \begin{bmatrix} (\frac{\Delta t^2}{2})^2 & \frac{\Delta t^2}{2} \Delta t \ \Delta t \frac{\Delta t^2}{2} & \Delta t^2 \end{bmatrix} \sigma^2_{x''}$$
$$ = \begin{bmatrix} \frac{\Delta t^4}{4} & \frac{\Delta t^3}{2} \ \frac{\Delta t^3}{2} & \Delta t^2 \end{bmatrix} \sigma^2_{x''} \tag{24}$$
$$ \text{假设 $x''$ - 是加速度 $a$,$Q = \begin{bmatrix} \frac{\Delta t^4}{4} & \frac{\Delta t^3}{2} \ \frac{\Delta t^3}{2} & \Delta t^2 \end{bmatrix} \sigma^2_{a}$} \tag{25}$$
测量噪声协方差$R$是标量(大小为$1 \times 1$的矩阵),定义为测量噪声的方差
$$R = \begin{matrix} \begin{matrix}& x\end{matrix} \ \begin{matrix}x\end{matrix} \begin{bmatrix}\sigma^2_{z}\end{bmatrix} \\ \end{matrix} = \sigma^2_{z} \tag{26}$$
Rust实现见此处
使用示例
let dt = 0.1;
let u = 2.0;
let std_dev_a = 0.25;
let std_dev_m = 1.2;
let t: nalgebra::SVector::<f32, 1000> = nalgebra::SVector::<f32, 1000>::from_iterator(float_loop(0.0, 100.0, dt));
let track = t.map(|t| dt*(t*t - t));
let mut kalman = Kalman1D::new(dt, u, std_dev_a, std_dev_m);
let mut measurement: Vec<f32> = vec![];
let mut predictions: Vec<f32>= vec![];
for (t, x) in t.iter().zip(track.iter()) {
// Add some noise to perfect track
let v: f32 = StdRng::from_entropy().sample::<f32, Standard>(Standard) * (50.0+50.0) - 50.0; // Generate noise in [-50, 50)
let z = kalman.H.x * x + v;
measurement.push(z);
// Predict stage
kalman.predict();
predictions.push(kalman.x.x);
// Update stage
kalman.update(z).unwrap();
}
println!("time;perfect;measurement;prediction");
for i in 0..track.len() {
println!("{};{};{};{}", t[i], track[i], measurement[i], predictions[i]);
}
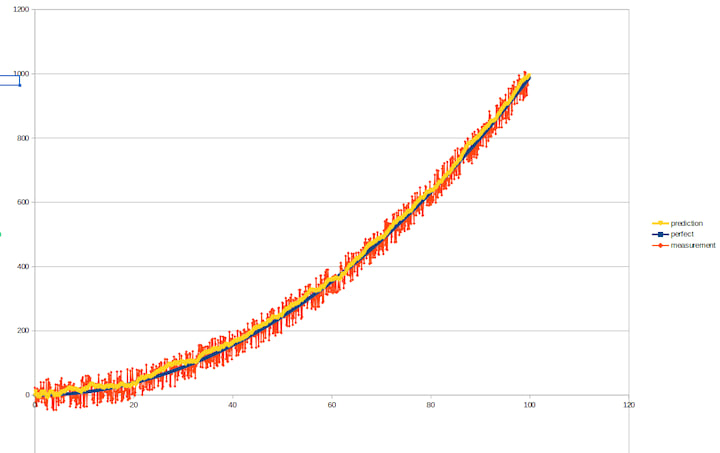
导出的图表看起来像这样
二维卡尔曼滤波器
考虑加速度运动,让我们写下其方程
考虑与$(13)$ - $(14)$相同的物理模型,让我们写下状态向量$\chi_{k}$
$$\chi_{k} = \begin{bmatrix} x_{k} \ y_{k} \ x'_ {k} \ y'_ {k} \end{bmatrix} = \begin{bmatrix} x_{k-1} + x'_ {k-1}\Delta t + \frac{x''_ {k-1}(\Delta t^2)}{2} \ y_{k-1} + y'_ {k-1}\Delta t + \frac{y''_ {k-1}(\Delta t^2)}{2} \ x'_ {k-1} + x''_ {k-1}\Delta t \ y'_ {k-1} + y''_ {k-1}\Delta t \end{bmatrix} \tag{27}$$
状态向量 $\chi_{k}$ 的矩阵形式
$$\chi_{k} = \begin{bmatrix} x_{k} \ y_{k} \ x'_ {k} \ y'_ {k} \end{bmatrix} = \begin{bmatrix} 1 & 0 & \Delta t & 0 \ 0 & 1 & 0 & \Delta t \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ⋅ \begin{bmatrix} x_{k-1} \ y_{k-1} \ x'_ {k-1} \ y'_ {k-1} \end{bmatrix} + \begin{bmatrix} \frac{\Delta t^2}{2} & 0 \ 0 & \frac{\Delta t^2}{2} \ \Delta t & 0 \ 0 & \Delta t \end{bmatrix} ⋅ \begin{bmatrix} x''_ {k-1} \ y''_{k-1} \end{bmatrix} = $$ $$ = \begin{bmatrix} 1 & 0 & \Delta t & 0 \ 0 & 1 & 0 & \Delta t \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ⋅ \chi_{k-1} + \begin{bmatrix} \frac{\Delta t^2}{2} & 0 \ 0 & \frac{\Delta t^2}{2} \ \Delta t & 0 \ 0 & \Delta t \end{bmatrix} ⋅ \begin{bmatrix} x''_ {k-1} \ y''_{k-1} \end{bmatrix} \tag{28}$$
$$ \text{假设 $x''$ 和 $y''$ - 是加速度 $a$,}$$
$$ a_{k-1} = \begin{bmatrix} x''_ {k-1} \ y''_{k-1} \end{bmatrix} \tag{29}$$
$$\chi_{k} = \begin{bmatrix} x_{k} \ y_{k} \ x'_ {k} \ y'_ {k} \end{bmatrix} = \begin{bmatrix} 1 & 0 & \Delta t & 0 \ 0 & 1 & 0 & \Delta t \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ⋅ \chi_{k-1} + \begin{bmatrix} \frac{\Delta t^2}{2} & 0 \ 0 & \frac{\Delta t^2}{2} \ \Delta t & 0 \ 0 & \Delta t \end{bmatrix} ⋅ a_{k-1} \tag{30}$$
仔细观察 $(16)$ 和 $(1)$,我们可以将转换矩阵 $A$ 和控制输入矩阵 $B$ 写成以下形式
$$A = \begin{bmatrix} 1 & 0 & \Delta t & 0 \\ 0 & 1 & 0 & \Delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \tag{31}$$
$$B = \begin{bmatrix} \frac{\Delta t^2}{2} & 0 \\ 0 & \frac{\Delta t^2}{2} \\ \Delta t & 0 \\ 0 & \Delta t \end{bmatrix} \tag{32}$$
让我们找到变换矩阵 $H$。根据 $(2)$ 和 $(19)$ - $(20)$
$$z_{k} = H⋅\chi_{k} + v_{k} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} ⋅\begin{bmatrix} x_{k} \\ y_{k} \\ {x'_ {k}} \\ {y'_ {k}} \end{bmatrix} + v_{k} \tag{33}$$
$$ H = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \tag{34}$$
过程噪声协方差矩阵 $Q$
$$Q = \begin{matrix} & \begin{matrix}x & y & x' & y' \end{matrix} \ \begin{matrix}x & y & x' & y' \end{matrix} & \begin{bmatrix} \sigma^2_{x} & 0 & \sigma_{x} \sigma_{x'} & 0 \\ 0 & \sigma^2_{y} & 0 & \sigma_{y} \sigma_{y'} \\ \sigma_{x'} \sigma_{x} & 0 & \sigma^2_{x'} & 0 \\ 0 & \sigma_{y'} \sigma_{y} & 0 & \sigma^2_{y'} \end{bmatrix} \\ \end{matrix} \tag{35}$$
$$\text{,其中} $$
$$ \text{其中,$\sigma_{x}$ - $x$ 方向位置的均方差} $$
$$ \text{其中,$\sigma_{y}$ - $y$ 方向位置的均方差} $$
$$ \text{其中,$\sigma_{x'}$ - $x$ 方向速度的均方差} $$
$$ \text{其中,$\sigma_{y'}$ - $y$ 方向速度的均方差} $$
由于我们已知 $(14)$,我们可以定义 $\sigma_{x}$,$\sigma_{y}$,$\sigma_{x'}$ 和 $\sigma_{y'}$ 如下
$$ \sigma_{x} = \sigma_{x''} \frac{\Delta t^2}{2} \tag{36}$$
$$ \sigma_{y} = \sigma_{y''} \frac{\Delta t^2}{2} \tag{37}$$
$$ \sigma_{x'} = \sigma_{x''} \Delta t \tag{38}$$
$$ \sigma_{y'} = \sigma_{y''} \Delta t \tag{39}$$
$$\text{,其中 $\sigma_{x''}$ 和 $\sigma_{y''}$ - 加速度的均方差(调整值)} $$
现在,过程噪声协方差矩阵$Q$可以定义为
$$ Q = \begin{bmatrix} (\sigma_{x''} \frac{\Delta t^2}{2})^2 & 0 & \sigma_{x''} \frac{\Delta t^2}{2} \sigma_{x''} \Delta t & 0 \\ 0 & (\sigma_{y''} \frac{\Delta t^2}{2})^2 & 0 & \sigma_{y''} \frac{\Delta t^2}{2} \sigma_{y''} \Delta t \\ \sigma_{x''} \frac{\Delta t^2}{2} \sigma_{x''} \Delta t & 0 & (\sigma_{x''} \Delta t)^2 & 0 \\ 0 & \sigma_{y''} \frac{\Delta t^2}{2} \sigma_{y''} \Delta t & 0 & (\sigma_{y''} \Delta t)^2 \end{bmatrix} = $$
$$ = \begin{bmatrix} (\sigma_{x''} \frac{\Delta t^2}{2})^2 & 0 & (\sigma_{x''})^2 \frac{\Delta t^2}{2} \Delta t & 0 \\ 0 & (\sigma_{y''} \frac{\Delta t^2}{2})^2 & 0 & (\sigma_{y''})^2 \frac{\Delta t^2}{2} \Delta t \\ (\sigma_{x''})^2 \frac{\Delta t^2}{2} \Delta t & 0 & (\sigma_{x''} \Delta t)^2 & 0 \\ 0 & (\sigma_{y''})^2 \frac{\Delta t^2}{2}\Delta t & 0 & (\sigma_{y''} \Delta t)^2 \end{bmatrix} = \text{| 知道 $x''$ 和 $y''$ - 加速度|} = $$ $$ = \begin{bmatrix} (\frac{\Delta t^2}{2})^2 & 0 & \frac{\Delta t^2}{2} \Delta t & 0 \\ 0 & (\frac{\Delta t^2}{2})^2 & 0 & \frac{\Delta t^2}{2} \Delta t \\ \frac{\Delta t^2}{2} \Delta t & 0 & \Delta t^2 & 0 \\ 0 & \Delta t \frac{\Delta t^2}{2} & 0 & \Delta t^2 \end{bmatrix} \sigma^2_{a''}$$
$$ = \begin{bmatrix} \frac{\Delta t^4}{4} & 0 & \frac{\Delta t^3}{2} & 0 \\ 0 & \frac{\Delta t^4}{4} & 0 & \frac{\Delta t^3}{2} \\ \frac{\Delta t^3}{2} & 0 & \Delta t^2 & 0 \\ 0 & \frac{\Delta t^3}{2} & 0 & \Delta t^2 \end{bmatrix} \sigma^2_{a''} \tag{40}$$
测量噪声的协方差 $R$ 是一个 $2 \times 2$ 的矩阵(因为有两个分量 - $x$ 和 $y$),并且定义为测量噪声的方差
$$R = \begin{matrix} \begin{matrix} & x & y \end{matrix} \ \begin{matrix}x & y \end{matrix} \begin{bmatrix}\sigma^2_{x} & 0 \\ 0 & \sigma^2_{y} \end{bmatrix} \\ \end{matrix} = \begin{bmatrix}\sigma^2_{x} & 0 \\ 0 & \sigma^2_{y} \end{bmatrix} \tag{41}$$
Rust实现在这里:链接
使用示例
let dt = 0.04; // 1/25 = 25 fps - just an example
let ux = 1.0;
let uy = 1.0;
let std_dev_a = 2.0;
let std_dev_mx = 0.1;
let std_dev_my = 0.1;
// Sample measurements
// Note: in this example Y-axis going from up to down
let xs = vec![311, 312, 313, 311, 311, 312, 312, 313, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 311, 311, 311, 311, 311, 310, 311, 311, 311, 310, 310, 308, 307, 308, 308, 308, 307, 307, 307, 308, 307, 307, 307, 307, 307, 308, 307, 309, 306, 307, 306, 307, 308, 306, 306, 306, 305, 307, 307, 307, 306, 306, 306, 307, 307, 308, 307, 307, 308, 307, 306, 308, 309, 309, 309, 309, 308, 309, 309, 309, 308, 311, 311, 307, 311, 307, 313, 311, 307, 311, 311, 306, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312];
let ys = vec![5, 6, 8, 10, 11, 12, 12, 13, 16, 16, 18, 18, 19, 19, 20, 20, 22, 22, 23, 23, 24, 24, 28, 30, 32, 35, 39, 42, 44, 46, 56, 58, 70, 60, 52, 64, 51, 70, 70, 70, 66, 83, 80, 85, 80, 98, 79, 98, 61, 94, 101, 94, 104, 94, 107, 112, 108, 108, 109, 109, 121, 108, 108, 120, 122, 122, 128, 130, 122, 140, 122, 122, 140, 122, 134, 141, 136, 136, 154, 155, 155, 150, 161, 162, 169, 171, 181, 175, 175, 163, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178];
let mut kalman = Kalman2D::new(dt, ux, uy, std_dev_a, std_dev_mx, std_dev_my);
// Assume that initial X,Y coordinates match the first measurement
kalman.x.x = xs[0] as f32;
kalman.x.y = ys[0] as f32;
let mut predictions: Vec<Vec<f32>> = vec![];
for (x, y) in xs.iter().zip(ys.iter()) {
// Considering that the measurements are noisy
let mx = *x as f32;
let my = *y as f32;
// Predict stage
kalman.predict();
predictions.push(vec![kalman.x.x, kalman.x.y]);
// Update stage
kalman.update(mx, my).unwrap();
}
println!("measurement X;measurement Y;prediction X;prediction Y");
for i in 0..xs.len() {
println!("{};{};{};{}", xs[i], ys[i], predictions[i][0], predictions[i][1]);
}
导出的图表看起来像这样
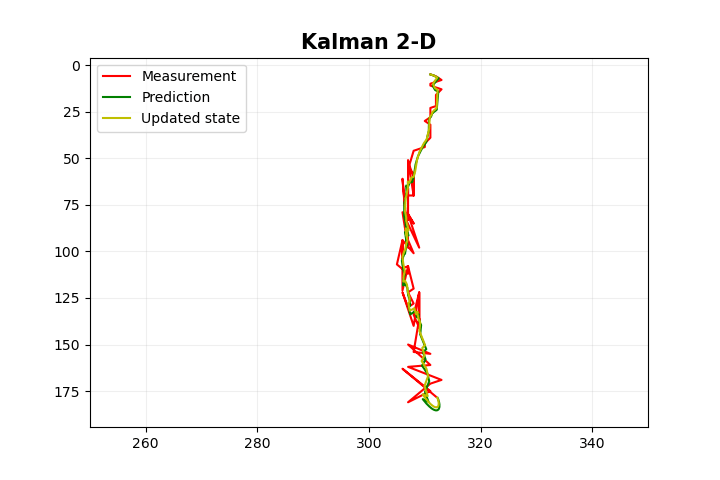
2D卡尔曼滤波器(包含加速度分量,无控制输入)
工作进行中
@待办:math-jax / Rust代码 / Rust测试 / 图表
如何使用
在您的Cargo.toml文件中添加依赖项
[package]
....
[dependencies]
...
kalman-rust = "0.2.2"
...
开始使用它,例如:Kalman2D
use kalman_rust::kalman::{
Kalman2D
};
fn main() {
let dt = 0.04; // 1/25 = 25 fps - just an example
let ux = 1.0;
let uy = 1.0;
let std_dev_a = 2.0;
let std_dev_mx = 0.1;
let std_dev_my = 0.1;
// Sample measurements
// Note: in this example Y-axis going from up to down
let xs = vec![311, 312, 313, 311, 311, 312, 312, 313, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 311, 311, 311, 311, 311, 310, 311, 311, 311, 310, 310, 308, 307, 308, 308, 308, 307, 307, 307, 308, 307, 307, 307, 307, 307, 308, 307, 309, 306, 307, 306, 307, 308, 306, 306, 306, 305, 307, 307, 307, 306, 306, 306, 307, 307, 308, 307, 307, 308, 307, 306, 308, 309, 309, 309, 309, 308, 309, 309, 309, 308, 311, 311, 307, 311, 307, 313, 311, 307, 311, 311, 306, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312, 312];
let ys = vec![5, 6, 8, 10, 11, 12, 12, 13, 16, 16, 18, 18, 19, 19, 20, 20, 22, 22, 23, 23, 24, 24, 28, 30, 32, 35, 39, 42, 44, 46, 56, 58, 70, 60, 52, 64, 51, 70, 70, 70, 66, 83, 80, 85, 80, 98, 79, 98, 61, 94, 101, 94, 104, 94, 107, 112, 108, 108, 109, 109, 121, 108, 108, 120, 122, 122, 128, 130, 122, 140, 122, 122, 140, 122, 134, 141, 136, 136, 154, 155, 155, 150, 161, 162, 169, 171, 181, 175, 175, 163, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178, 178];
// Assume that initial X,Y coordinates match the first measurement
let ix = xs[0] as f32; // Initial state for X
let iy = ys[0] as f32; // Initial state for Y
let mut kalman = Kalman2D::new_with_state(dt, ux, uy, std_dev_a, std_dev_mx, std_dev_my, ix, iy);
let mut predictions: Vec<Vec<f32>> = vec![];
let mut updated_states: Vec<Vec<f32>> = vec![];
for (x, y) in xs.iter().zip(ys.iter()) {
// Considering that the measurements are noisy
let mx = *x as f32;
let my = *y as f32;
// Predict stage
kalman.predict();
let state = kalman.get_vector_tate();
predictions.push(vec![state.x, state.y]);
// Update stage
kalman.update(mx, my).unwrap();
let updated_state = kalman.get_vector_tate();
updated_states.push(vec![updated_state.x, updated_state.y]);
}
println!("measurement X;measurement Y;prediction X;prediction Y;updated X;updated Y");
for i in 0..xs.len() {
println!("{};{};{};{};{};{}", xs[i], ys[i], predictions[i][0], predictions[i][1], updated_states[i][0], updated_states[i][1]);
}
}
参考
- Greg Welch 和 Gary Bishop,《卡尔曼滤波器简介》,2006年7月24日
- Alex Becker的《卡尔曼滤波器简介》
- 维基百科上的卡尔曼滤波器
- 状态转移矩阵
- Rahmad Sadli的Python实现
备注:
我在GitHub的MathJax markdown中显示矩阵时遇到了一些困难。如果您有更好的方法,欢迎提出
依赖项
~4.5MB
~89K SLoC