95个版本 (53个稳定版)
| 10.1.3 | 2024年5月26日 |
|---|---|
| 9.3.1 | 2024年5月7日 |
| 9.0.0 | 2024年3月9日 |
| 8.0.1 | 2024年2月21日 |
| 0.5.0 | 2021年7月20日 |
#42 in 无标准库
每月 106 次下载
用于 2 个Crates(通过 four-bar)
80KB
1.5K SLoC
EFD Rust库
椭圆傅里叶描述符 (EFD) 的Rust实现。此包实现了1D/2D/3D EFD及其相关函数。
此实现完全安全,并支持 no-std + alloc 环境。
关键词别名
- 椭圆傅里叶分析 (EFA)
- 椭圆傅里叶函数 (EFF)
重新描述新的封闭曲线的示例
let curve = vec![
[0., 0.],
[1., 1.],
[2., 2.],
[3., 3.],
[2., 2.],
[1., 1.],
];
assert!(efd::util::valid_curve(&curve).is_some());
let described_curve = efd::Efd2::from_curve(curve, false).recon(20);
谐波数可以通过 efd::Efd::from_curve_harmonic() 方法设置。以下图显示了使用1-8个谐波重建的二维封闭曲线。
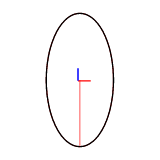
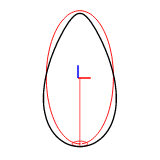
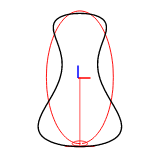
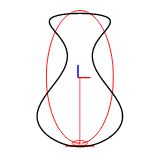
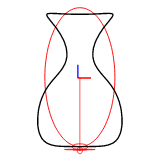
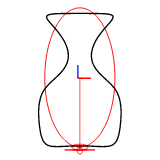
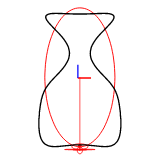
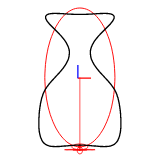
示例图像
2D和3D封闭曲线
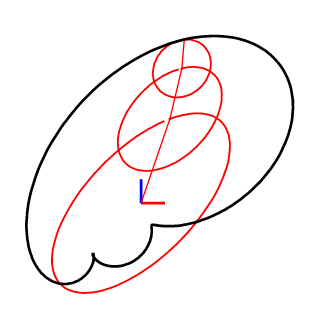
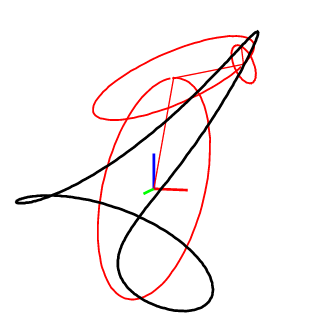
2D和3D开放曲线
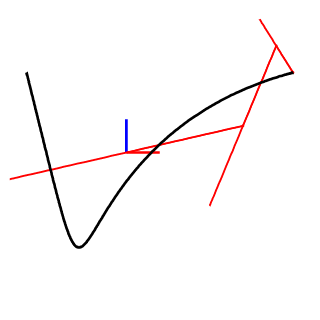
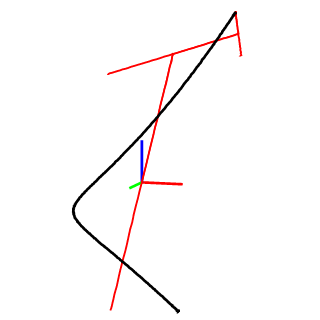
姿态EFD将曲线与姿态(单位向量)结合,以描述每个点的方向。
2D开放曲线及其完整重建
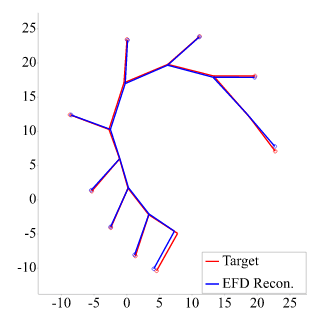
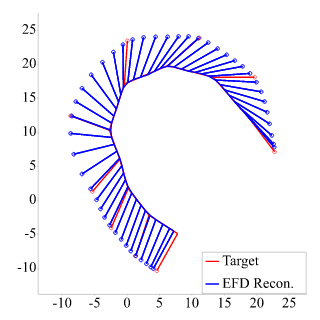
参考文献
原始
- Kuhl, FP and Giardina, CR (1982). Elliptic Fourier features of a closed contour. Computer graphics and image processing, 18(3), 236-258. https://doi.org/10.1016/0146-664X(82)90034-X
我的应用
- Chang, Y., Chang, JL., Lee, JJ. (2024). Atlas-Based Path Synthesis of Planar Four-Bar Linkages Using Elliptical Fourier Descriptors. In: Okada, M. (eds) Advances in Mechanism and Machine Science. IFToMM WC 2023. Mechanisms and Machine Science, vol 149. Springer, Cham. https://doi.org/10.1007/978-3-031-45709-8_20
- Chang, Y., Chang, JL. & Lee, JJ. Path Synthesis of Planar Four-bar Linkages for Closed and Open Curves Using Elliptical Fourier Descriptors. J Mech Sci Technol (2024). http://doi.org/10.1007/s12206-024-0436-y
依赖项
~4MB
~85K SLoC