pathfinding_astar

这是我对之前使用A星寻路算法的工作的增强和推广。

主要区别在于，在我的六边形工作中，库负责确定路径遍历的有效相邻节点，用户必须指定特定的坐标系和六边形空间的边界。例如，使用偏移几何体时，可以使用以下方式返回最佳路径

let start_node: (i32, i32) = (0, 0);
let mut nodes: HashMap<(i32, i32), f32> = HashMap::new();
nodes.insert((0, 0), 1.0);
// snip inserting all the nodes
let end_node: (i32, i32) = (3, 3);
let min_column = -1;
let max_column = 4;
let min_row = -1;
let max_row = 4;
let orientation = HexOrientation::FlatTopOddUp;
let path = astar_path(
    start_node,
    nodes,
    end_node,
    min_column,
    max_column,
    min_row,
    max_row,
    orientation,
);

如您所见，有min和max边界，这些边界必须提供，以及一个方向（您的六边形是平顶还是尖顶？哪个列/行已被移位以允许平整镶嵌？）。

这种新的方法旨在与任何“旅行点”或节点的排列一起工作。实现这一点需要使用一种数据结构，其中节点知道其邻居是什么以及它们有多远，而不是库即时计算这些值——这意味着它适用于多种几何体和抽象路线。

什么是A星？

对于许多相互连接的节点，A星涉及使用所谓的启发式（称为权重W）来引导计算，以便快速找到从一个点到另一个点的最佳路径。

如果我们从一个起点S移动到终点E，我们可以选择两条路径，到O1或到O2。

                        Length:22             W:4
                 S ----------------------> O1
                 |                         |
                 |                         |
        Length:5 |                         | Length:4
                 |                         |
                 ▼                         ▼
                 O2 ---------------------> E
            W:1          Length:20            W:2

每个点都有一个相关的权重W，这是一个旨在引导算法的通用度量。

为了找到最佳路径，我们发现了从起点S到给定点的可用路径，从S到该点的距离，并创建一个沿路径移动的A星得分。例如

• S和O1之间的距离是22
• 从 S 移动到 O1 的 A-Star 分数是移动距离与权重点的和，即 22 + 4 = 26

然后我们考虑从 S 到 O2 的替代路线

• S 和 O2 之间的距离是 5
• 因此 A-Star 分数是 5 + 1 = 6

我们可以看到，目前最优的路线是从 S 移动到 O2（它具有较低的 A-Star 分数）——因为移动到 O2 具有更好的 A-Star 分数，我们首先询问这个点。

从 O2 我们发现我们可以遍历到 E

• 现在覆盖的总距离是 20 + 5 = 25
• A-Star 分数是总距离和 E 权重的和，25 + 2 = 27

到目前为止，我们已经探索了

• S 到 O1，A-Star 分数为 26
• S 到 O2 到 E，A-Star 分数为 27

由于我们还有一条具有更好 A-Star 分数的路线，我们将其扩展，从 O1 到 E

• 总距离 22 + 4 = 26
• A-Star 分数是 26 + 2 = 28

在这个简单的用例中，我们已经探索了所有路径，并找到了最终的分数

• S 到 O1 到 E，A-Star 分数为 28
• S 到 O2 到 E，A-Star 分数为 27

现在我们知道哪条路径更好，通过 O2 移动具有更好的最终 A-Star 分数（它更小）。

这个想法是，对于大量点和路径，某些路线不会探索，因为它们的 A-Star 分数会高得多，这减少了搜索时间。

使用此库

给定一组节点，您可以通过提供以下信息找到从一个节点到另一个节点的最优化路径（如果存在）：

• 您的起始节点
• 您的终点或目标节点
• 包含它们的权重启发式以及它们各自的邻居和他们之间的距离的节点图。
  • 注意，权重设置为较大的权重值表示难以遍历的节点。

如果不存在路由，库将返回 None，否则您将获得 Some(Vec<T>)，其中包含最佳路径的节点标签，其中类型 T 与您用来唯一标记节点的内容相对应。注意 T 必须实现 Eq、Hash、Debug、Copy 和 Clone 特性，通常我使用 i32 或 (i32, i32) 作为标签，这满足这个条件。

请注意，如果您的节点权重非常相似，则算法可能会给出第二或第三高度优化的路径，而不是最佳路径。调整您的权重是确保最佳结果的方法，但在大多数情况下，第二/第三路线已经足够好——这源于多个节点最终具有相同的 A-Star 分数的情况，其中首先被处理的第一个节点为其末端节点生成良好的 A-Star 分数，然后返回。

因此，通常选择一个类型 T 来标记您的每个节点，指定您的起始节点和结束节点，然后通过以下函数与您所有节点的映射一起，您可以找到路径

pub fn astar_path<T>(
	start_node: T,
	nodes: HashMap<T, (Vec<(T, f32)>, f32)>,
	end_node: T,
) -> Option<Vec<T>>

其中 nodes 必须还包含您的 start_node 和 end_node。HashMap 的键也是您选择的用于唯一识别节点的标签，值元组有两个部分

• 一个具有相同类型标签的邻居向量以及该邻居与当前键之间的距离作为一个 f32
• 一个 f32 权重，该权重将引导算法

当与网格等一起工作时

________________________
| L:12| L:13| L:14| L:15|
| W:5 | W:8 | W:9 | W:4 |
|_____|_____|_____|_____|
| L:8 | L:9 | L:10| L:11|
| W:1 | W:1 | W:4 | W:3 |
|_____|_____|_____|_____|
| L:4 | L:5 | L:6 | L:7 |
| W:1 | W:9 | W:14| W:6 |
|_____|_____|_____|_____|
| L:0 | L:1 | L:2 | L:3 |
| W:1 | W:7 | W:3 | W:7 |
|_____|_____|_____|_____|

标记为 L:0 的正方形需要了解其邻居 L:1 和 L:4，从数据的角度来看，我们可以将其表达为

let start: i32 = 0;
let end: i32 = 15;
// Keys are the labels to uniquely identify a node
// Values contain a vec of neighbours you can move to with the distance to them, and an `f32` to weight to node.
// Note the distance from one square to its neighbour is the same so in our Vec tuple we use the unit distance `1.0`
let mut nodes: HashMap<i32, (Vec<(i32, f32)>, f32)> = HashMap::new();
// Node L:0 has neighbours L:4 with distance 1.0 and L:1 with distance 1.0, and a weight of 1.0
nodes.insert(0, (vec![(4, 1.0), (1, 1.0)], 1.0));
// Node L:1 has 3 neighbours and is itself weighted 7.0
nodes.insert(1, (vec![(5, 1.0), (2, 1.0), (0, 1.0)], 7.0));
nodes.insert(2, (vec![(6, 1.0), (3, 1.0), (1, 1.0)], 3.0));
// snip - the rest of this data is in the test `grid_like_path()`
let path = astar_path(start, nodes, end).unwrap();
let actual = vec![0, 4, 8, 9, 10, 11, 15];
assert_eq!(actual, path);

同样，如果事先知道哪些六边形相邻，这个库可以应用于六边形空间。

             _______
            /   0   \
    _______/         \_______
   /  -1   \       1 /   1   \
  /         \_______/         \
  \       1 /   q   \       0 /
   \_______/         \_______/
   /  -1   \       r /   1   \
  /         \_______/         \
  \       0 /   0   \      -1 /
   \_______/         \_______/
           \      -1 /
            \_______/

使用类似（轴向）标签的 (q, r) 标记节点及其可能邻居

let mut nodes: HashMap<(i32, i32), (Vec<((i32, i32), f32)>, f32)> = HashMap::new();
nodes.insert((0, 0), (vec![((0, 1), 1.0), ((1, 0), 1.0), ((1, -1), 1.0), ((0, -1), 1.0), ((-1, 0), 1.0), ((-1, 1), 1.0)], 1.0));
// snip

再次，从中心一个六边形到另一个六边形的距离总是相同的，所以我们使用了单位距离 1.0。

最后，它可以应用于更抽象的空间，考虑以下道路

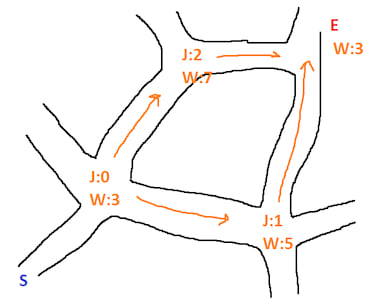
从外部来看，您可以使用一些数据来根据交通量计算每个交叉口/道路的权重，并且如果您知道每条道路的长度，您可以计算从 S 到 E 的最佳路径——就像一个卫星导航设备。

更进一步，您可以将权重视为复合值，其中您根据许多不同的因素进行计算，例如，您可以考虑不同类型的道路受到速度限制并且有不同的交通量水平。

let dirt_road_base_weight = 13.0; // slow
let main_road_base_weight = 5.0;  // fast

let dirt_road_traffic_weight = 4.0; // less busy
let main_road_traffic_weight = 15.0; // very busy

let dirt_road_weight = dirt_road_base_weight + dirt_road_traffic_weight;
let main_road_weight = main_road_base_weight + main_road_traffic_weight;

一个完整的抽象示例可能如下所示

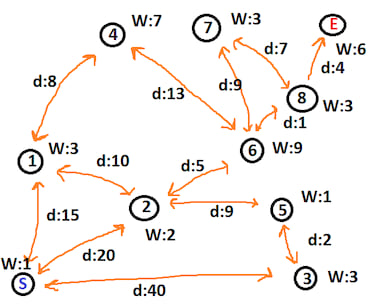
我们从节点 S（标签 0）开始，希望到达节点 E（标签 9）。每个节点都有一个权重 W，每条线都有一个距离 d。我们可以构造所需的数据如下

let start_node: i32 = 0;
let end_node: i32 = 9;
let mut nodes: HashMap<i32, (Vec<(i32, f32)>, f32)> = HashMap::new();
nodes.insert(0, (vec![(1, 15.0), (2, 20.0), (3, 40.0)], 1.0));
nodes.insert(1, (vec![(4, 8.0), (2, 10.0), (0, 15.0)], 3.0));
nodes.insert(2, (vec![(1, 10.0), (6, 5.0), (5, 9.0), (0, 20.0)], 2.0));
nodes.insert(3, (vec![(5, 2.0), (0, 40.0)], 3.0));
nodes.insert(4, (vec![(6, 13.0), (1, 8.0)], 7.0));
nodes.insert(5, (vec![(2, 9.0), (3, 2.0)], 1.0));
nodes.insert(6, (vec![(7, 9.0), (8, 1.0), (4, 13.0), (2, 5.0)], 9.0));
nodes.insert(7, (vec![(8, 7.0), (6, 9.0)], 3.0));
nodes.insert(8, (vec![(7, 7.0), (6, 1.0), (9, 4.0)], 3.0));
nodes.insert(9, (vec![(8, 4.0)], 6.0));
let path = astar_path(start_node, nodes, end_node).unwrap();
let actual = vec![0, 2, 6, 8, 9];
assert_eq!(actual, path);