13个版本 (1个稳定版)
| 1.0.0 | 2022年3月27日 |
|---|---|
| 0.9.0 | 2022年1月22日 |
| 0.8.4 | 2022年1月22日 |
| 0.7.0 | 2022年1月1日 |
| 0.4.2 | 2021年10月12日 |
#416 在 算法 中
每月下载量 23次
135KB
1.5K SLoC
致谢:我想感谢Red Blob Games,他们有一套非常棒的指南/教程,详细介绍了六边形空间及其相关的几何形状,这对我将概念Rust化帮助极大。
hexagonal_pathfinding_astar
这个库是A*路径查找算法的实现,针对特定加权六边形集合进行优化。它的目的是计算从中心六边形到目标六边形的最优路径,在遍历过程中,从中心六边形到下一个六边形沿垂直于六边形边的直线移动。该算法已针对偏移、轴向和立方坐标系实现,并提供了一系列辅助函数,可用于在坐标系之间进行转换、计算六边形之间的距离等。
它在以下方面有所不同:它遵循一个惯例,即六边形的度量反映了在时间内穿越距离的难度,称为复杂性(不要问我为什么我没有将其命名为速度)。
例如
___________
/ ^ \
/ | \
/ c | \
\ | /
\ ▼ /
\___________/
对于一个完美的平齐六边形网格,从中心到边中点的距离在所有方向上都是相同的。这个库类似于你醒来在一个“六边形世界”中,你只能从中心一个六边形直接移动到另一个六边形,但是当距离是静态的,你会发现当你从一个六边形跨越边界到另一个六边形时,你会突然加速,而不是缓慢行走。
通用示例:想象你从家里出来,站在路边。你想要去商店,有两个选择,一个在左边,一个在右边。它们离你都是100米,但是如果你向左走,你将不得不穿过一条繁忙的街道,而向右走则通往一个更安静的市区,那里你可以骑自行车。为了尽快完成购物,你想向右走。这就是我所说的复杂性,它不是六边形宽度的度量,所有距离都是相同的,而是一个衡量你穿越它的速度的度量。
另一个例子,假设你是一名RPG游戏中的角色,站在一个表示开阔空间的六边形上。如果你向东移动到下一个六边形,你将站在一片森林中。在你起始的六边形中,你将以较快的速度移动一段时间,一旦你越过六边形边界进入森林,你将更慢地向该六边形的中心移动。
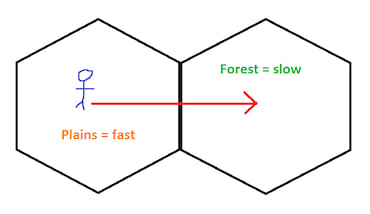
这个库主要关注计算在某个奇异的六边形世界中沿着严格路径移动的情况。
我创建它是为了我现在正在使用Bevy引擎开发一个游戏。这是一个程序化六边形世界,每个六边形都可以是不同的生物群落,例如山脉、平原、沙漠。生物群落会影响你穿越六边形的速度,并且以实时方式播放,这样你不仅能感受到穿越由六边形表示的空间宽度,还能感受到地下地形的影响。
局限性
- 请保持节点位置小于
i32::MAX/2和大于i32::MIN/2,否则可能会因为溢出而发生不良事件,并且你将不会得到一个合理/有效的路径。
目录
A-Star简介
这是我关于A-Star的非常基本的分解,它使用传统的距离而不是我的自定义复杂性(你可以用它来确定在乡村地区驾车到达某个目的地应该选择哪些道路)。
如果我们从一个起点S移动到终点E,我们有两个路径可以选择穿越,到O1或到O2。
Length:22 W:4
S ----------------------> O1
| |
| |
Length:5 | | Length:4
| |
▼ ▼
O2 ---------------------> E
W:1 Length:20 W:2
每个点都有一个相关的权重W,它是一个旨在引导算法的通用度量。
为了找到最佳路径,我们从起点S发现可用的路线,从S到给定点的距离,并创建一个沿路径移动的A-Star得分。例如
S和O1之间的距离是22- 从
S到O1的A-Star得分为移动的距离与点的权重的总和,即22 + 4 = 26
然后我们考虑从S到O2的替代路线
S和O2之间的距离是5- A*得分因此为
5 + 1 = 6
我们可以看到,当前最优化路线是从 S 移动到 O2(它有更低的A*得分)——因为移动到 O2 有更好的A*得分,所以我们首先询问这个点。
从 O2 我们发现我们可以遍历到 E
- 现在覆盖的总距离为
20 + 5 = 25 - A*得分是总距离和
E的权重的总和,25 + 2 = 27
到目前为止,我们已经探索了
S到O1,A*得分为26S到O2到E,A*得分为27
由于我们仍然有更好的A*得分的路线可用,我们扩展了它,从 O1 到 E
- 总距离为
22 + 4 = 26 - A*得分为
26 + 2 = 28
现在我们知道哪条路径更好了,通过 O2 移动具有更好的最终A*得分(它更小)。
这个想法是,对于大量点和路径,某些路径将不会探索,因为它们的A*得分会高得多,这减少了搜索时间。在这个存储库的 docs 目录中,有一些关于六边形网格空间的手动计算,展示了这个过程。
传统A*与六边形世界怪异性的区别
传统的A*使用 distance 和 weight(通常称为启发式)来确定最佳路径,这鼓励它尽可能高效地寻找通向单个终点的路径。权重是测量点与终点之间距离的度量。距离可以非常大。
对于这种六边形排列,每个六边形都保持一个称为权重的启发式,它指导算法,但距离是静态的,每个六边形具有相同的宽度。相反,我添加了一个新的启发式,称为 complexity,它是遍历六边形的难度,其中高复杂性表示昂贵的路径。重要的是要注意,移动是从一个六边形的中心移动到另一个六边形的中心,这意味着移动的复杂性基于起始六边形的复杂性值的一半加上目标六边形复杂性值的一半。
权重是六边形距离终点的线性度量,在库中计算,而不是提供——它实际上是您从 hex-Current 到 hex-End 需要跳过的次数。
从图形上讲,我们可以用一个网格来表示复杂度,用 complexity 表示为 C,用 weights 表示为 W,它基于每个节点到 E 节点的距离(此示例使用每个六边形的北和东北边缘的轴心坐标)。
_________
/ 0 \
/ \
_________/ C:1 \_________
/ -1 \ W:2 2 / 1 \
/ \ / \
_________/ C:2 \_________/ C:14 \_________
/ -2 \ W:3 2 / 0 \ W:1 1 / 2 \
/ \ / \ / 🔴E \
/ C:1 \_________/ C:1 \_________/ C:1 \
\ W:4 2 / -1 \ W:2 1 / 1 \ W:0 0 /
\ / \ / \ /
\_________/ C:7 \_________/ C:15 \_________/
/ -2 \ W:3 1 / 0 \ W:1 0 / 2 \
/ \ / 🟩S \ / \
/ C:8 \_________/ C:1 \_________/ C:1 \
\ W:4 1 / -1 \ W:2 0 / 1 \ W:1 -1 /
\ / \ / \ /
\_________/ C:6 \_________/ C:14 \_________/
/ -2 \ W:3 0 / 0 \ W:2 -1 / 2 \
/ \ / \ / \
/ C:1 \_________/ C:2 \_________/ C:1 \
\ W:4 0 / -1 \ W:3 -1 / 1 \ W:2 -2 /
\ / \ / \ /
\_________/ C:3 \_________/ C:1 \_________/
\ W:4 -1 / 0 \ W:3 -2 /
\ / \ /
\_________/ C:1 \_________/
\ W:4 -2 /
\ /
\_________/
您会看到,在库中计算的权重会在 E 周围形成一个波前,并且随着距离的增加而增加。这在两个相邻节点的复杂度相差不大时有助于引导算法。
节点 S,(0, 0) 和其南部相邻节点之间的移动复杂度是半复杂度的总和,即 (1 * 0.5) + (2 * 0.5) = 1.5。这些半值是算法在 A-Star 计算中使用以模拟在某种边界(如穿越田野然后上山)上从中心到中心的移动。
使用轴心实现从 S 移动到 E 揭示出最佳路径是
_________
/ 2 \
/ 🔴E \
/ C:1 \
\ W:0 0 /
\ /
_________ \_________/
/ 0 \ / 2 \
/ 🟩S \ / \
/ C:1 \ / C:1 \
\ W:2 0 / \ W:1 -1 /
\ / \ /
\_________/ \_________/
/ 0 \ / 2 \
/ \ / \
/ C:2 \_________/ C:1 \
\ W:3 -1 / 1 \ W:2 -2 /
\ / \ /
\_________/ C:1 \_________/
\ W:3 -2 /
\ /
\_________/
六边形网格和方向
六边形网格可以以不同的方式呈现,这会影响可发现的相邻六边形用于路径遍历 - 六边形发现对于此算法至关重要,它需要探索它可以前往的方向并为它们评分。
轴心坐标
轴心坐标使用 q 作为列,r 作为行的约定。在下面的示例中,r 是一条对角行。对于尖角向上 facing 的六边形布局,计算保持完全相同,因为你实际上只是将网格旋转了 30 度,使得 r 水平,而 q 对角。
_______
/ 0 \
_______/ \_______
/ -1 \ 1 / 1 \
/ \_______/ \
\ 1 / q \ 0 /
\_______/ \_______/
/ -1 \ r / 1 \
/ \_______/ \
\ 0 / 0 \ -1 /
\_______/ \_______/
\ -1 /
\_______/
在这个对齐中找到节点的邻居相对简单,对于一个给定的节点在 (q, r) 位置,从北开始并按顺时针方向移动
north = (q, r + 1)
north-east = (q + 1, r)
south-east = (q + 1, r - 1)
south = (q, r - 1)
south-west = (q - 1, r)
north-west = (q - 1, r + 1)
这些可以通过公共辅助函数以编程方式找到,其中网格有一个圆形边界,由从 (0,0) 原点(边界确保您不会发现网格区域外的节点)的最大环数表示
pub fn node_neighbours_axial(
source: (i32, i32),
count_rings: i32,
) -> Vec<(i32, i32)>
立方坐标
您可以通过三个主要轴表示六边形网格。我们用 x、y 和 z 表示轴。立方坐标系非常有用,因为某些计算不能通过其他坐标系进行(它们不包含足够的数据),幸运的是,有方法将其他系统转换为立方,以使计算变得容易/可能。
立方网格的结构如下
_______
/ 0 \
_______/ \_______
/ -1 \ -1 1 / 1 \
/ \_______/ \
\ 0 1 / x \ -1 0 /
\_______/ \_______/
/ -1 \ y z / 1 \
/ \_______/ \
\ 1 0 / 0 \ 0 -1 /
\_______/ \_______/
\ 1 -1 /
\_______/
要从 (x, y, z) 开始,按顺时针方向找到节点的邻居
north = (x, y - 1, z + 1)
north-east = (x + 1, y - 1, z)
south-east = (x + 1, y, z - 1)
south = (x, y + 1, z - 1)
south-west = (x - 1, y + 1, z)
north-west = (x - 1, y, z + 1)
可以通过一个公共辅助函数以编程方式找到这些邻居,其中网格具有圆形边界,由从 (0,0) 原点计数的最大环数表示(这确保您不会返回我们网格区域之外的节点)
pub fn node_neighbours_cubic(
source: (i32, i32, i32),
count_rings_from_origin: i32,
) -> Vec<(i32, i32, i32)>
此外,在立方排列中,还有一个辅助函数可以找到给定源节点周围的环上的节点(可以将其视为视野半径)
pub fn node_ring_cubic(
source: (i32, i32, i32),
radius: i32,
) -> Vec<(i32, i32, i32)>
偏移坐标
偏移假定所有六边形都绘制在一个平面上,其中原点位于左下角(从理论上讲,您可以有负坐标扩展到其他三个象限,但我在这里还没有测试过)。
每个节点都有一个标签定义其位置,称为 (列, 行)。
平坦顶部 - 奇数列上移
_______
/ \
_______/ (1,1) \_______
/ \ / \
/ (0,1) \_______/ (2,1) \
\ / \ /
\_______/ (1,0) \_______/
/ \ / \
/ (0,0) \_______/ (2,0) \
\ / \ /
\_______/ \_______/
列的偏移量会改变我们发现附近节点的方式。例如,如果我们取节点(0,0)并希望发现其北东方向的节点(1,0),我们只需将 列 值加一。
然而,如果我们取节点(1,0)并希望发现其北东方向的节点(2,1),我们必须将 列 值和 行 值都加一。即计算取决于奇数列是向上还是向下偏移。
对于偶数列的节点,我们可以这样计算节点的邻居
north = (column, row + 1)
north-east = (column + 1, row)
south-east = (column + 1, row - 1)
south = (column, row -1)
south-west = (column - 1, row - 1)
north-west = (column - 1, row)
对于奇数列的节点,节点的邻居可以这样找到
north = (column, row + 1)
north-east = (column + 1, row + 1)
south-east = (column + 1, row)
south = (column, row -1)
south-west = (column - 1, row)
north-west = (column - 1, row + 1)
可以通过一个公共辅助函数以编程方式找到这些邻居,其中网格在空间中的边界由最小和最大值表示,同样这确保您不会返回网格区域之外的节点
pub fn node_neighbours_offset(
source: (i32, i32),
orientation: &HexOrientation,
min_column: i32,
max_column: i32,
min_row: i32,
max_row: i32,
) -> Vec<(i32, i32)>
其中 orientation 必须是 HexOrientation::FlatTopOddUp
平坦顶部 - 奇数列下移
_______ _______
/ \ / \
/ (0,1) \_______/ (2,1) \
\ / \ /
\_______/ (1,1) \_______/
/ \ / \
/ (0,0) \_______/ (2,0) \
\ / \ /
\_______/ (1,0) \_______/
\ /
\_______/
列的偏移量会改变我们发现附近节点的方式。例如,如果我们取节点(0,0)并希望发现其北东方向的节点(1,1),我们将 列 和 行 值都加一。
然而,如果我们取节点(1,1)并希望发现其北东方向的节点(2,1),我们只需将 列 值加一。
对于偶数列的节点,我们可以这样计算节点的邻居
north = (column, row + 1)
north-east = (column + 1, row + 1)
south-east = (column + 1, row)
south = (column, row -1)
south-west = (column - 1, row)
north-west = (column - 1, row + 1)
对于奇数列的节点,节点的邻居可以这样找到
north = (column, row + 1)
north-east = (column + 1, row)
south-east = (column + 1, row - 1)
south = (column, row -1)
south-west = (column - 1, row - 1)
north-west = (column - 1, row)
可以通过一个公共辅助函数以编程方式找到这些邻居,其中网格在空间中的边界由最小和最大值表示
pub fn node_neighbours_offset(
source: (i32, i32),
orientation: &HexOrientation,
min_column: i32,
max_column: i32,
min_row: i32,
max_row: i32,
) -> Vec<(i32, i32)>
其中 orientation 必须是 HexOrientation::FlatTopOddDown
尖顶 - 奇数行右移
(由于尖顶六边形在 ASCII 中很难绘制,所以现在是时候用一些 MSPaint 了)
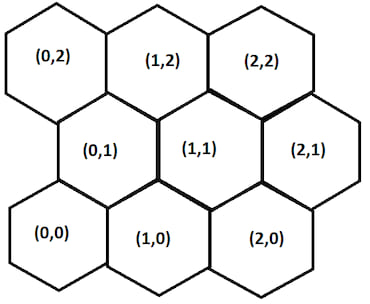
行的偏移量会改变我们发现附近节点的方式。例如,如果我们取节点(0,0)并希望发现其北东方向的节点(0,1),我们将 行 值加一。
然而,如果我们取节点(0,1)并希望发现其北东方向的节点(1,2),我们必须将 列 和 行 值都加一。
对于偶数行的节点,我们可以这样计算节点的邻居
north-east = (column, row + 1)
east = (column + 1, row)
south-east = (column, row - 1)
south-west = (column - 1, row - 1)
west = (column -1, row)
north-west = (column - 1, row + 1)
对于奇数行中的节点,可以找到其邻居节点。
north-east = (column + 1, row + 1)
east = (column + 1, row)
south-east = (column + 1, row - 1)
south-west = (column, row - 1)
west = (column -1, row)
north-west = (column, row + 1)
尖顶 - 奇数行向左偏移
(由于尖顶六边形在 ASCII 中很难绘制,所以现在是时候用一些 MSPaint 了)
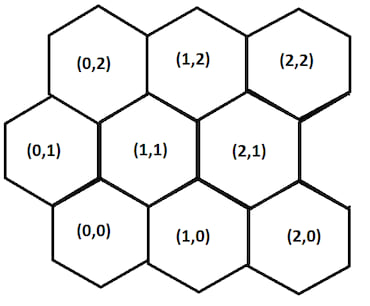
行偏移改变了我们查找附近节点的方式。例如,如果我们取节点(0,0)并希望发现其东北方向的节点(1,1),我们需要将列和行的值各加一。
然而,如果我们取节点(1,1)并希望发现其东北方向的节点(1,2),我们只需要将行的值加一。
对于偶数行的节点,我们可以这样计算节点的邻居
north-east = (column + 1, row + 1)
east = (column + 1, row)
south-east = (column + 1, row - 1)
south-west = (column, row - 1)
west = (column -1, row)
north-west = (column, row + 1)
对于奇数行中的节点,可以找到其邻居节点。
north-east = (column, row + 1)
east = (column + 1, row)
south-east = (column, row - 1)
south-west = (column - 1, row - 1)
west = (column -1, row)
north-west = (column - 1, row + 1)
您应该使用什么坐标系?
如果您正在构建一个正方形/矩形网格,我认为偏移布局是最容易开始使用的,它只是类似于x-y轴上的列和行,还有一些列/行的偏移。
如果您正在构建一个圆形网格,那么轴对称和立方坐标系统无疑是最好的,因为它们的坐标系自然适合圆形空间。
您可以使用轴对称和立方坐标系统来构建正方形/矩形网格,通过创建一个非常大的圆并使用极高复杂度的值在空间的四个边缘标记出六边形,但这只是存储内存的浪费,对于复杂的路径查找,算法可能会浪费时间探测角落。
如何使用
Cargo.toml
[dependencies]
hexagonal_pathfinding_astar = "1.0"
偏移示例
是xyz.rs的一部分
use hexagonal_pathfinding_astar::*;
// you are here
let start_node: (i32, i32) = (0, 0);
// keys are nodes, values are your measure of 'complexity' to traverse it
let mut nodes: HashMap<(i32, i32), f32> = HashMap::new();
nodes.insert((0, 0), 1.0);
nodes.insert((0, 1), 1.0);
nodes.insert((0, 2), 1.0);
nodes.insert((0, 3), 3.0);
nodes.insert((1, 0), 2.0);
nodes.insert((1, 1), 9.0);
nodes.insert((1, 2), 4.0);
nodes.insert((1, 3), 2.0);
nodes.insert((2, 0), 2.0);
nodes.insert((2, 1), 6.0);
nodes.insert((2, 2), 8.0);
nodes.insert((2, 3), 9.0);
nodes.insert((3, 0), 3.0);
nodes.insert((3, 1), 4.0);
nodes.insert((3, 2), 5.0);
nodes.insert((3, 3), 2.0);
// you want to go here
let end_node: (i32, i32) = (3, 3);
// the 'exclusive' limit of grid size
let min_column = -1;
let max_column = 4;
let min_row = -1;
let max_row = 4;
// the hexagon arrangement you are using
let orientation = HexOrientation::FlatTopOddUp;
let best = astar_offset::astar_path(start_node, nodes, end_node, min_column, max_column, min_row, max_row, orientation);
// answer using above data = [(0,0), (0,1), (0,2), (1,2), (2,3), (3,3)]
// the manual calculation for this can be found under `docs/calculations_done_manually.md`
立方示例
use hexagonal_pathfinding_astar::*;
// you are here
let start_node: (i32, i32, i32) = (0, 0, 0);
// keys are nodes, values are the complexity
let mut nodes: HashMap<(i32, i32, i32), f32> = HashMap::new();
nodes.insert((0, 0, 0), 1.0);
nodes.insert((0, -1, 1), 1.0);
nodes.insert((1, -1, 0), 15.0);
nodes.insert((1, 0, -1), 14.0);
nodes.insert((0, 1, -1), 2.0);
nodes.insert((-1, 1, 0), 6.0);
nodes.insert((-1, 0, 1), 7.0);
nodes.insert((0, -2, 2), 1.0);
nodes.insert((1, -2, 1), 14.0);
nodes.insert((2, -2, 0), 1.0);
nodes.insert((2, -1, -1), 1.0);
nodes.insert((2, 0, -2), 1.0);
nodes.insert((1, 1, -2), 1.0);
nodes.insert((0, 2, -2), 1.0);
nodes.insert((-1, 2, -1), 3.0);
nodes.insert((-2, 2, 0), 1.0);
nodes.insert((-2, 1, 1), 8.0);
nodes.insert((-2, 0, 2), 1.0);
nodes.insert((-1, -1, 2), 2.0);
// you want to go here
let end_node: (i32, i32, i32) = (2, -2, 0);
// it's a circular grid with a limited number of rings
let rings = 2;
let best = astar_cubic::astar_path(start_node, nodes, end_node, rings);
// answer = vec![(0, 0, 0),(0, 1, -1),(1, 1, -2),(2, 0, -2),(2, -1, -1),(2, -2, 0)]