5个版本 (3个破坏性更新)
| 0.5.0 | 2024年8月16日 |
|---|---|
| 0.4.0 | 2024年5月4日 |
| 0.3.1 | 2024年3月30日 |
| 0.3.0 | 2024年3月30日 |
| 0.2.0 | 2024年3月24日 |
在数学类别中排名第212
每月下载量157
34KB
429 行
lazyivy
lazyivy是一个Rust包,它提供了使用Runge-Kutta方法解决形如 dY/dt = F(t, Y) 的初值问题的工具,其中 Y 是一个向量,而 t 是一个标量。
算法使用实现 Iterator 的结构 RungeKutta 来实现。目前实现了以下Runge-Kutta方法,未来还将添加更多。
- 欧拉1
- Ralston 2
- Huen-Euler 2(1)
- Bogacki-Shampine 3(2)
- Fehlberg 4(5)
- Dormand-Prince 5(4)
(p 是方法的阶数,而 (p*) 是嵌入式误差估计器的阶数,如果有的话。)
Lazy积分
RungeKutta 实现了 Iterator 特性。每次调用 .next() 会将迭代推进到下一个Runge-Kutta 步,并返回一个元组 (t, Y),其中 t 是因变量,而 Y 是 Array1<f64>。
请注意,每个Runge-Kutta 步包含 s 个内部 阶段。使用lazyivy,目前无法访问这些内部阶段的积分值。每次调用 .next() 都返回每个步骤的最终结果,这是对所有阶段的求和。
Runge-Kutta的懒实现意味着你可以以不同的方式消费迭代器。例如,你可以使用.last()来保留最终结果,使用.collect()来收集所有步骤的状态,使用.map()来将迭代器与其他迭代器链式调用等。你也可以选择在for循环中使用它,并实现你自己的逻辑来修改步长或自定义停止条件。
API是不稳定的。它是活跃的,并且处于开发中。
用法
在将lazyivy添加到Cargo.toml之后,使用提供的构建器创建一个初始值问题。以下是一个示例,展示如何解决Brusselator。
\frac{d}{dt} \left[ \begin{array}{c}
y_1 \\ y_2 \end{array}\right] = \left[\begin{array}{c}1 - y_1^2 y_2 - 4 y_1
\\ 3y_1 - y_1^2 y_2 \end{array} \right]
use lazyivy::RungeKutta;
use ndarray::{array, ArrayView1, ArrayViewMut1};
fn brusselator(_t: &f64, y: ArrayView1<f64>, mut result: ArrayViewMut1<f64>) {
result[0] = 1. + y[0].powi(2) * y[1] - 4. * y[0];
reuslt[1] = 3. * y[0] - y[0].powi(2) * y[1];
}
fn main() {
let t0: f64 = 0.;
let y0 = array![1.5, 3.];
let absolute_tol = array![1.0e-4, 1.0e-4];
let relative_tol = array![1.0e-4, 1.0e-4];
// Instantiate a integrator for an ODE system with adaptive step-size
// Runge-Kutta. The `builder` method takes in as argument the evaluation
// function and the predicate function (that determines when to stop). You
// need to call `build()` to consume the builder and return a `RungeKutta`
// struct.
let mut integrator = RungeKutta::builder(brusselator, |t, _| *t > 40.)
.initial_condition(t0, y0)
.initial_step_size(0.025)
.method("dormandprince", true) // `true` for adaptive step-size
.tolerances(absolute_tol, relative_tol)
.set_max_step_size(0.25)
.build()
.unwrap();
// For adaptive algorithms, you can use this to improve the initial guess
// for the step size.
integrator.set_step_size(&integrator.guess_initial_step());
// Perform the iterations and print each state.
for item in integrator {
println!("{:?}", item); // Prints (t, array[y1, y2]) for each step.
}
}
绘图的结果如下,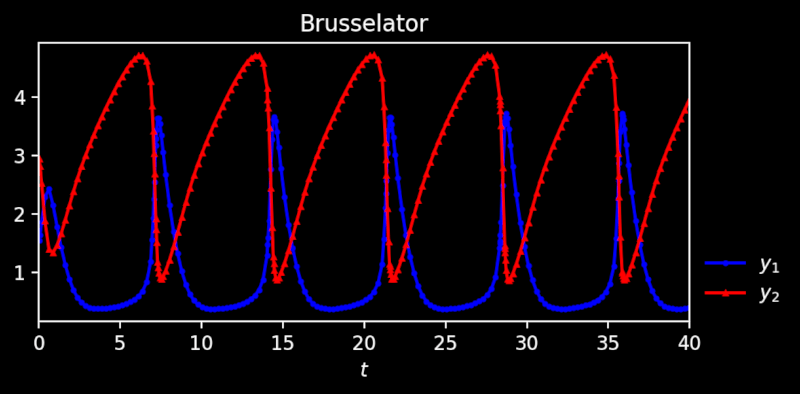
同样,你也可以为其他问题做同样的事情,例如,对于洛伦兹系统,定义评估函数
fn lorentz_attractor(_t: &f64, y: ArrayView1<f64>, mut result: ArrayViewMut1<f64>) {
result[0] = 10. * (y[1] - y[0]);
result[1] = y[0] * (28. - y[2]) - y[1];
result[2] = y[0] * y[1] - 8. / 3. * y[2];
}
你还可以使用闭包来捕获环境并包装你的评估。也就是说,如果你有一个函数
fn lorentz_attractor(
x: f64,
y: f64,
z: f64,
sigma: f64,
beta: f64,
rho: f64
) -> Array1<f64> {
array![
sigma * (y - x),
x * (rho - z) - y,
x * y - beta * z,
]
}
你不能直接将其传递给RungeKutta::builder()。但你可以将其包装在一个闭包中。例如
let sigma = 10.;
let beta = 8. / 3.;
let rho: 28.;
let eval_closure = |_t, y, result| { // here result is mut
// Closure captures the environment and wraps the function signature
result = lorentz_attractor(y[0], y[1], y[2], sigma, beta, rho);
};
let integrator = RungeKutta::builder(eval_closure, |t, _| *t > 20.)
... // other parameters
.build();
这之所以可行,是因为没有修改其环境的闭包可以强制转换为Fn。因此,这种模式不适用于修改其环境的闭包。一般来说,你可以使用任何评估函数和停止条件,但它们必须是Fn(&f64, ArrayView1<f64>, ArrayViewMut1<f64>)和Fn(&f64, ArrayView1<f64>) -> bool,分别。
以下是一个显示洛伦兹系统结果的图像。
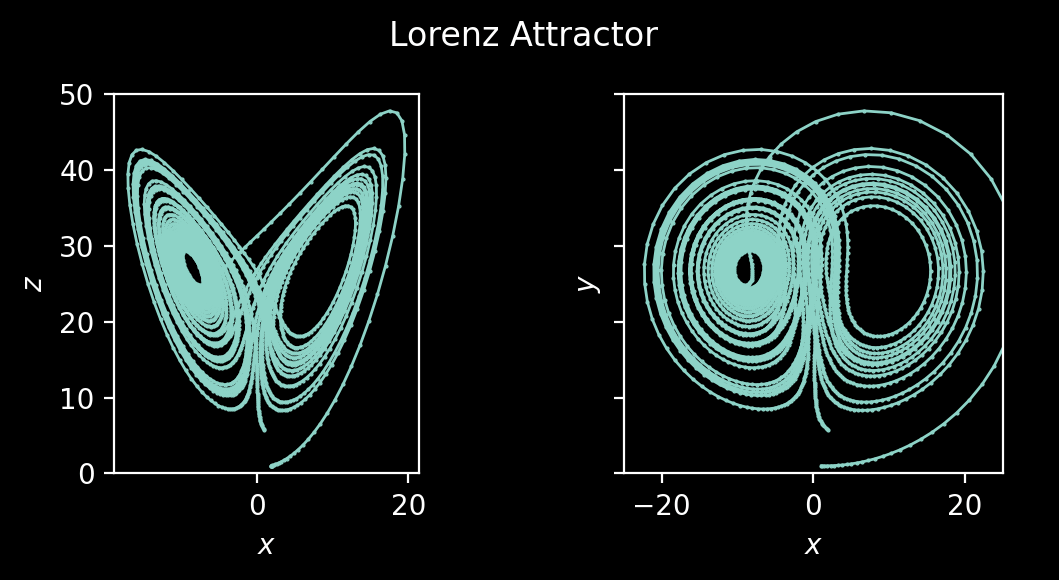
就地修改(自0.5.0版本起)
在上面的洛伦兹系统示例中,我使用array!宏创建了一个新数组。然而,在实际应用中,我建议你使用评估函数来修改传递给函数的result数组。
例如,同样的例子可以写成
fn lorentz_attractor(
x: f64,
y: f64,
z: f64,
sigma: f64,
beta: f64,
rho: f64,
result: ArrayViewMut1<f64>, // Mutate this argument in-place.
) {
result[0] = sigma * (y - x);
result[1] = x * (rho - z) - y;
result[2] = x * y - beta * z;
}
然后你可以使用适当的签名将其包装在闭包中。
let sigma = 10.;
let beta = 8. / 3.;
let rho: 28.;
let eval_closure = |_t, y, result| { // here result is mut
lorentz_attractor(y[0], y[1], y[2], sigma, beta, rho, result);
// ^-----
// Added result as an argument
};
这样你就可以避免每次函数调用时都进行分配。
为了简化这一更改,从v0.5.0版本开始,之前通配符参数F的签名由Fn(&f64, &Array1<f64>) -> Array1<f64>更改为Fn(&f64, ArrayView1<f64>, ArrayViewMut1<f64>)。
由于Rust不允许存在多个可变引用,这个更改意味着RungeKutta不再线程安全。但是,这应该没问题,因为Runge-Kutta迭代是顺序的,不容易多线程化。
待办事项
- 添加更好的测试。
- 基准测试。
依赖项
~1.6–2.1MB
~43K SLoC