6个版本
| 0.2.1 | 2024年7月24日 |
|---|---|
| 0.2.0 | 2024年7月3日 |
| 0.1.3 | 2024年6月19日 |
| 0.1.2 | 2024年4月26日 |
| 0.1.1 | 2024年3月29日 |
#79 in 数学
每月195次下载
125KB
2K SLoC
icao-wgs84
一个用于在WGS84椭球上执行几何计算的库,见图1。
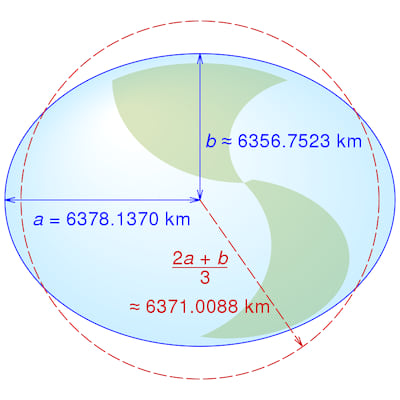
图1 WGS84椭球(非比例图)
自从WGS84被Navstar全球定位系统(GPS)采用,以及美国前总统里根1983年决定在民航客机KAL 007因导航错误误入禁飞区被苏联拦截机击落之后,WGS84已经成为卫星导航的既定标准。
本库使用ICAO WGS 84实施手册第3-1表中的WGS84主要参数。
大地测量导航
椭球面上两点之间的最短路径是大地线——平面几何中直线段或球面上大圆的等价物,见图2。
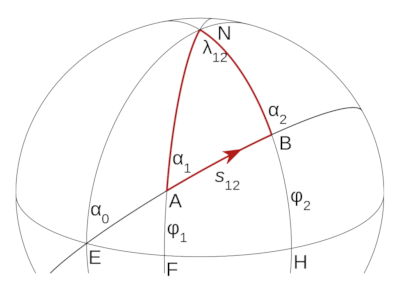
图2 A与B两点间的大地线
本库使用椭球面上的大地线与辅助球面上的大圆之间的对应关系,以及三维向量来计算
- 两点之间大地线的初始方位角和长度;
- 相对于大地线的位置沿航线距离和横穿航线距离;
- 以及大地线对的交点。
设计
本库基于Charles Karney的GeographicLib库。
与GeographicLib类似,它将大地线路径建模为辅助球面上的大圆。然而,它还使用向量来计算沿航线距离、横穿航线距离和大地线之间的交点。
Ellipsoid类表示旋转椭球。
静态的 WGS84_ELLIPSOID 表示 WGS 84 Ellipsoid,这是由 Geodesic From 特性用于在 WGS 84 Ellipsoid 上创建 Geodesic 的。
库依赖于以下 crate
- angle-sc - 用于定义
Angle、Degrees和Radians并执行三角计算; - unit-sphere - 用于定义
LatLong并执行大圆和矢量计算。 - icao_units - 用于定义
Metres和NauticalMiles并在它们之间进行转换。
图 3 类图
库被声明为 no_std,因此它可以在嵌入式应用程序中使用。
示例
计算大地线初始方位角和长度
计算两点之间初始方位角(又称航向)和距离(海里)。
use icao_wgs84::*;
let istanbul = LatLong::new(Degrees(42.0), Degrees(29.0));
let washington = LatLong::new(Degrees(39.0), Degrees(-77.0));
let (azimuth, length) = calculate_azimuth_and_geodesic_length(&istanbul, &washington, &WGS84_ELLIPSOID);
let azimuth_degrees = Degrees::from(azimuth);
println!("Istanbul-Washington initial azimuth: {:?}", azimuth_degrees.0);
let distance_nm = NauticalMiles::from(length);
println!("Istanbul-Washington distance: {:?}", distance_nm);
计算沿航迹和横航迹距离
在两点之间创建一个 Geodesic,然后计算第三点相对于 Geodesic 的沿航迹和横航迹距离。
此示例基于 C. F. F. Karney 的以下回复: https://sourceforge.net/p/geographiclib/discussion/1026621/thread/21aaff9f/#8a93。
预期的纬度和经度来自 Karney 的回复
最终结果 54.92853149711691 -21.93729106604878
注意:横航迹距离(xtd)为负,因为雷克雅未克位于 Geodesic 的右侧。
横航迹距离是
- 对于位于
Geodesic左侧的位置为正; - 对于位于
Geodesic右侧的位置为负; - 对于位于
Geodesic精度范围内的位置为零。
use icao_wgs84::*;
use angle_sc::is_within_tolerance;
let istanbul = LatLong::new(Degrees(42.0), Degrees(29.0));
let washington = LatLong::new(Degrees(39.0), Degrees(-77.0));
let g1 = Geodesic::from(&istanbul, &washington);
let azimuth_degrees = Degrees::from(g1.azimuth(Metres(0.0)));
println!("Istanbul-Washington initial azimuth: {:?}", azimuth_degrees.0);
let distance_nm = NauticalMiles::from(g1.length());
println!("Istanbul-Washington distance: {:?}", distance_nm);
let reyjavik = LatLong::new(Degrees(64.0), Degrees(-22.0));
// Calculate geodesic along track and across track distances to 1mm precision.
let (atd, xtd, iterations) = g1.calculate_atd_and_xtd(&reyjavik, Metres(1e-3));
assert!(is_within_tolerance(3928788.572, atd.0, 1e-3));
assert!(is_within_tolerance(-1010585.9988368, xtd.0, 1e-3));
println!("calculate_atd_and_xtd iterations: {:?}", iterations);
let position = g1.lat_long(atd);
assert!(is_within_tolerance(
54.92853149711691,
Degrees::from(position.lat()).0,
128.0 * f64::EPSILON
));
assert!(is_within_tolerance(
-21.93729106604878,
Degrees::from(position.lon()).0,
2048.0 * f64::EPSILON
));
另外注意:此示例使用 1mm 精度以匹配 Karney 的结果。
实际上,精度应从位置精度确定。
更高的精度需要更多的迭代,因此计算结果需要更长的时间。
计算大地线交点
创建两个 Geodesic,每个都位于两点之间,然后计算从大地线起点到其交点的距离。
此示例基于 C. F. F. Karney 的以下回复: https://sourceforge.net/p/geographiclib/discussion/1026621/thread/21aaff9f/#fe0a
预期的纬度和经度来自 Karney 的回复
最终结果 54.7170296089477 -14.56385574430775
注意:Karney 的解决方案要求所有 4 个位置都位于以交点为中心的同一半球。
此解决方案没有这个要求。
use icao_wgs84::*;
use angle_sc::is_within_tolerance;
let istanbul = LatLong::new(Degrees(42.0), Degrees(29.0));
let washington = LatLong::new(Degrees(39.0), Degrees(-77.0));
let reyjavik = LatLong::new(Degrees(64.0), Degrees(-22.0));
let accra = LatLong::new(Degrees(6.0), Degrees(0.0));
let g1 = Geodesic::from((&istanbul, &washington));
let g2 = Geodesic::from((&reyjavik, &accra));
// Calculate the intersection point position
let result = calculate_intersection_point(&g1, &g2, Metres(1e-3));
// Get the intersection point position
let lat_lon = result.unwrap();
assert!(is_within_tolerance(54.7170296089477, lat_lon.lat().0, 1e-6));
assert!(is_within_tolerance(-14.56385574430775, lat_lon.lon().0, 1e-6));
测试
集成测试使用 Charles Karney 的 大地线测试数据 来验证 WGS84 椭球体上位置之间的大地线方位角和距离计算。使用以下命令运行测试
cargo test -- --ignored
贡献
如果您想通过代码或文档进行贡献,最好的开始方式是 贡献指南。如果您有任何问题,请随时提问。但请遵守我们的 行为准则。
许可证
icao-wgs84 由 MIT 许可证提供,请参阅 LICENSE。
依赖项
约 4.5MB
约 90K SLoC