6个版本
| 0.2.1 | 2024年7月24日 |
|---|---|
| 0.2.0 | 2024年7月1日 |
| 0.1.3 | 2024年6月19日 |
| 0.1.2 | 2024年4月26日 |
| 0.1.0 | 2024年2月25日 |
#314 in 数学
208 每月下载量
在 icao-wgs84 中使用
89KB
1.5K SLoC
unit-sphere
一个用于在球面上进行几何计算的库。
该库通过结合球面三角学和矢量几何,在单位球面上执行大圆航线,见图1。
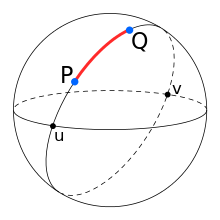
图1 大圆航线
大圆是球面上两点之间的最短路径。
它是平面几何中直线在球面上的对应物。
球面三角学
可以使用球面三角学计算两点之间的大圆路径。
大圆的航向(起始方位角)可以从起始点和终点的纬度和经度计算得出。
而大圆距离也可以通过使用哈夫纳公式从起始点和终点的纬度和经度计算得出。
得到的距离(以弧度为单位)可以通过将距离乘以以所需单位测量的地球半径转换为所需单位。
矢量几何
球面上的点和极点可以用3D矢量表示。
与球面三角学相比,使用矢量进行许多计算要简单得多。
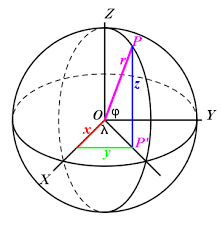
图2 球面矢量坐标
例如,可以从点和大圆极矢量之间的点积计算出点到大圆的横切距离。而大圆的交点可以通过极矢量的叉积简单地计算得出。
设计
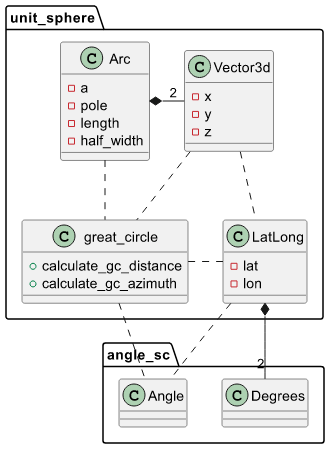
great_circle 模块执行球面三角学计算,而 vector 模块执行矢量几何计算。
图3 类图
该库声明为无标准库,因此可以用于嵌入式应用程序。
示例
以下示例计算两个大圆弧Arc的交集。
这些值来自Charles Karney对两大地形线相交的原始解决方案。
use unit_sphere::{Arc, Degrees, LatLong, calculate_intersection_point};
use angle_sc::is_within_tolerance;
let istanbul = LatLong::new(Degrees(42.0), Degrees(29.0));
let washington = LatLong::new(Degrees(39.0), Degrees(-77.0));
let reyjavik = LatLong::new(Degrees(64.0), Degrees(-22.0));
let accra = LatLong::new(Degrees(6.0), Degrees(0.0));
let arc1 = Arc::try_from((&istanbul, &washington)).unwrap();
let arc2 = Arc::try_from((&reyjavik, &accra)).unwrap();
let intersection_point = calculate_intersection_point(&arc1, &arc2).unwrap();
let lat_long = LatLong::from(&intersection_point);
// Geodesic intersection latitude is 54.7170296089477
assert!(is_within_tolerance(54.72, lat_long.lat().0, 0.05));
// Geodesic intersection longitude is -14.56385574430775
assert!(is_within_tolerance(-14.56, lat_long.lon().0, 0.02));
贡献
如果您想通过代码或文档进行贡献,请从贡献指南开始。如果您有任何问题,请随时提出。只是请遵守我们的行为准则。
许可证
unit-sphere在MIT许可证下提供,请参阅LICENSE。
依赖项
~4MB
~87K SLoC