Lib.rs

› 科学
#embedding #algorithm #umap #ann #dimension-reduction #data-points #dataset

bin+lib annembed

Rust实现的Umap风格的降维

作者：jpboth

15个版本

0.1.3 2024年5月13日
0.1.1 2024年2月9日
0.1.0 2023年9月25日
0.0.11 2023年7月3日
0.0.1 2021年7月2日

#18 in 科学


在4 个包中使用

MIT/Apache

415KB
5K SLoC

数据嵌入工具和相关数据分析或聚类

该包主要提供库的形式（有关在csv文件中嵌入数据的二进制文件嵌入的文档）

  1. 从t-Sne（2008）到Umap（2018）的数据嵌入工具的一些变体。

    我们的实现是参考文献中提到的各种嵌入算法的混合。

  • 图是通过在： hnsw_rs 中实现的Hnsw最近邻算法初始化的。
    这允许在嵌入数据时免费进行子采样，只考虑较少密集的层（上层）。这通常对应于2%-4%的子采样，但可以保证采样点和其最近采样邻居之间的距离已知。因此，hnsw结构还允许通过考虑不断增加的层数进行迭代/分层初始化嵌入。

  • 为嵌入构建的初步图使用距离的指数函数（如在Umap中），但保持与邻居的概率归一化约束（如在T-sne中）。可以通过考虑距离函数的幂来调节初始边权重（请参阅模块EmbedderParams中的文档）。
    - 增加或减少每个节点周围点局部密度的影响。图形没有对称化（除非在用扩散映射初始化嵌入时，在这种情况下，它像t-sne或LargeVis一样进行）。我们使用扩散映射算法（Lafon-Keller-Coifman）。

  • 我们还使用初始布局的交叉熵优化，但在计算嵌入边的柯西权重时考虑每个点的初始局部密度估计。相应的“困惑度”分布会实时估计。（请参阅模块EmbedderParams中的文档）。

  • 我们提供了一个嵌入连续性的试探性评估，以帮助在选择给定数据集的运行之间不同的结果时进行选择。这详细说明在函数 Embedder::get_quality_estimate_from_edge_length 的文档中，并在示例目录中进行了说明。

  1. 一些副产物

    • 密集矩阵和/或行压缩矩阵的范数近似和近似奇异值分解的实现，如svdapprox模块和Halko-Tropp论文中所述（参见Tsvd）。

    • 数据内在维度的估计，如以下所述
      Levina E.和Bickel P.J NIPS 2004。参见论文。

    • Hnsw结构图的中心性估计，如以下所述：Radovanovic M.，Nanopoulos A.和Ivanovic M.参见论文

    • 扩散映射实现。

    • 到拓扑数据分析Julia包Ripserer.jl的链接（参见crate中的Julia目录）。
      邻域内或从降维投影图中点之间的距离矩阵可以输出以进行进一步处理（参见模块fromhnsw::toripserer中的文档）。因此，可以在crate Julia目录中提供的Julia函数的帮助下生成云点的持久性图/条形码（同时提供相关csv文件结果中嵌入数据的可视化）。

构建

Blas选择

crate提供了3个功能，可以选择openblas-static、intel-mkl-static或openblas-system，如ndarray-linalg crate中定义。

编译

  • 使用cargocargo build --release --features="openblas-static"进行静态链接，链接rust下载的openblas

  • 使用cargocargo build --release --features="intel-mkl-static"链接到mkl intel库（mkl将被自动下载，参见ndarray-linalg crate的README.md）

  • 使用cargocargo build --release --features="openblas-system"链接到系统安装的openblas库。在这种情况下，您必须有一个编译了INTERFACE64=0的openblas库，对应于32位fortran整数。

您也可以在默认功能中添加您想要的功能。

simd

在Intel CPU上，您可以在默认功能中添加simdeez_f功能，或使用命令< strong>cargo build --release --features="openblas-system,simdeez_f"。在非Intel CPU上，可以使用< strong>stdsimd功能或< strong>"cargo build --release --features="openblas-system,stdsimd"。请注意，< strong>stdsimd需要nightly编译器。

Julia

Julia脚本提供图形功能。
可以从julia下载Julia。然后必须安装julia源中提及的< strong>using子句中的包，参见Pkg。然后在Julia REPL中，< strong>include("annembed.jl")提供访问Annembed.localPersistency和Annembed.projectedPersistency函数。可能需要运行< em>export LD_PRELOAD=/lib/x86_64-linux-gnu/libstdc++.so.6或等效命令，以强制Julia使用您的C++库，因为GPU驱动程序和GLFW.jl之间存在微妙的交互参见。

结果

给出了24核（32线程）i9笔记本电脑、64GB内存的计时。

嵌入器示例

示例的源代码在相应的目录中。

  1. MNIST数字数据库参见mnist-digits

    它包含70000个784像素的手写数字图像

    • 通过近似奇异值分解初始化。

    运行时间为11秒（系统时间），其中3秒系统时间（100秒CPU）用于ann构建。

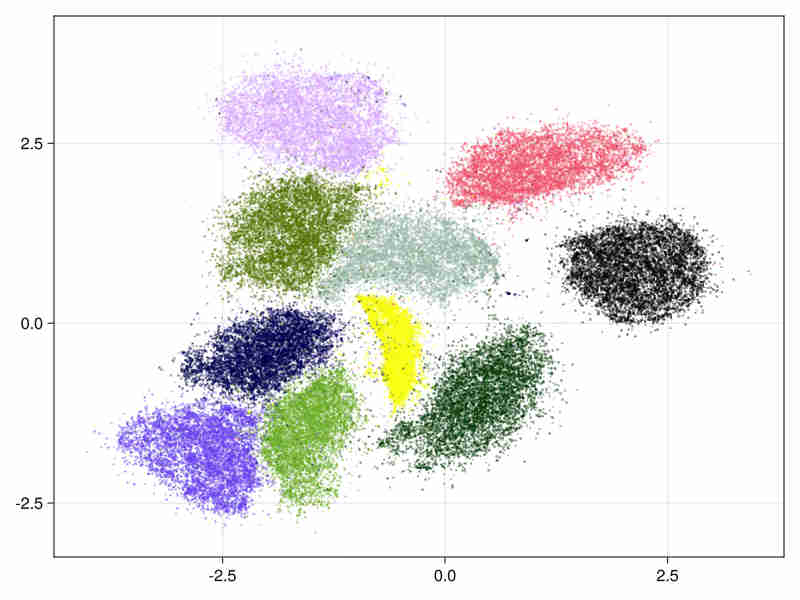
    mnist

    • 分层初始化

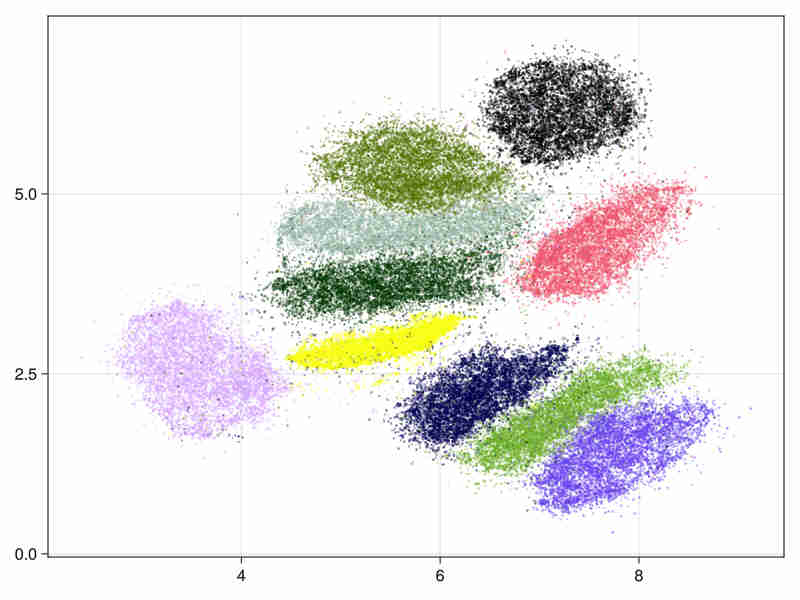
    mnist

    运行时间为11秒（334秒CPU时间），其中3秒用于ann构建。

    • 估计的数据内在维度为18.5，标准偏差取决于点：7.2，考虑每个点周围的排序邻居，在9-20名第一名的范围内。

  2. MNIST时尚数据库参见mnist-fashion

    它包含70000张服装图像。

    • 通过近似奇异值分解初始化。

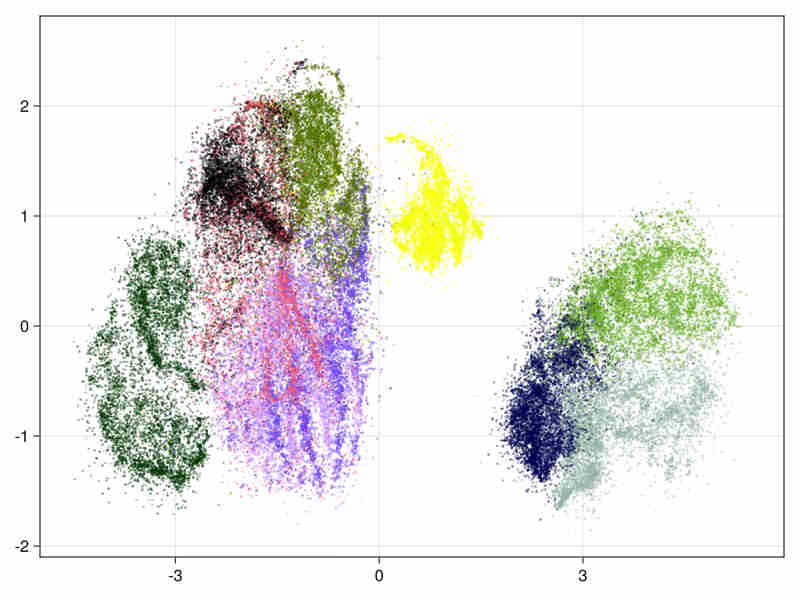
    mnist

    系统时间：14秒，CPU时间428秒

    • 分层初始化（这在用于大数据嵌入中很有用，我们通过先初始化Hnsw结构的深层填充的上层来加速过程）。

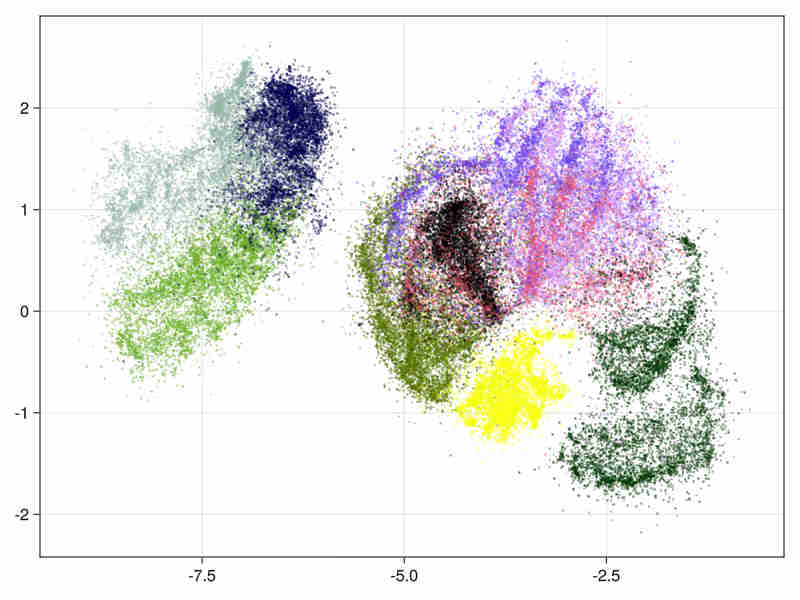
    mnist

    系统时间：15秒，CPU时间466秒

    • 数据估计的内禀维度为21.9，标准差取决于点，为12.2，考虑每个点周围第9至第20个排名的排序邻居。

  3. 希格斯玻色子 Cf Higgs数据

    它由11百万个28维的浮点向量组成。首先我们在前21列上运行，排除物理学家构建的用于辅助机器学习任务中区分的最后7个变量，然后在28个变量上运行。

    在两种情况下，我们都使用分层初始化。第一次遍历使用从第1层（包括）到上层各层，运行了200个批次。因此，第一批次运行在大约460000个节点上。然后，在1100万个点上完成了40个批次。

    两种情况下的运行时间都在2小时左右（Hnsw构建45分钟，熵迭代75分钟）

    • 21和28变量完整数据的图像

      由于数据量较大，质量评估需要数据子采样（参见示例和结果）。此外，可以在Higgs.jl Notebook中找到基本的数据探索，以评估嵌入的质量通过随机投影。

      21变量图像

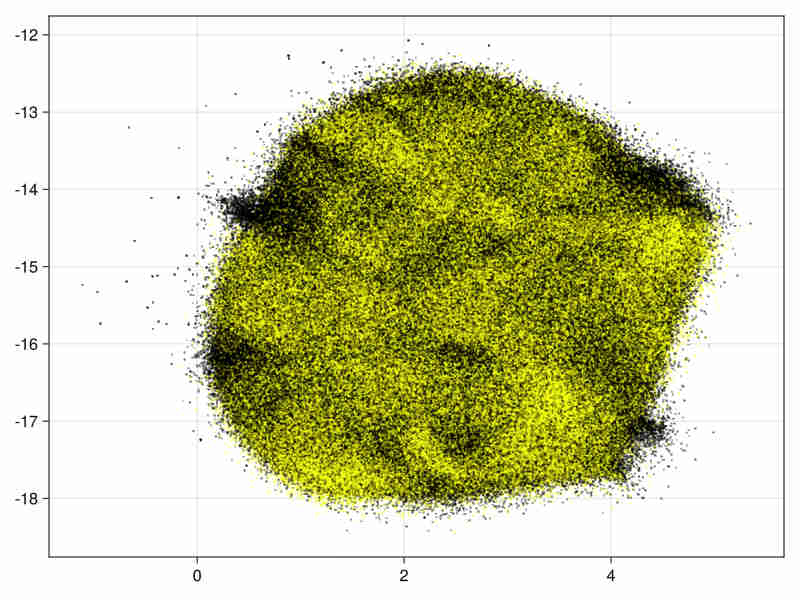
    higgs-21

    28变量图像

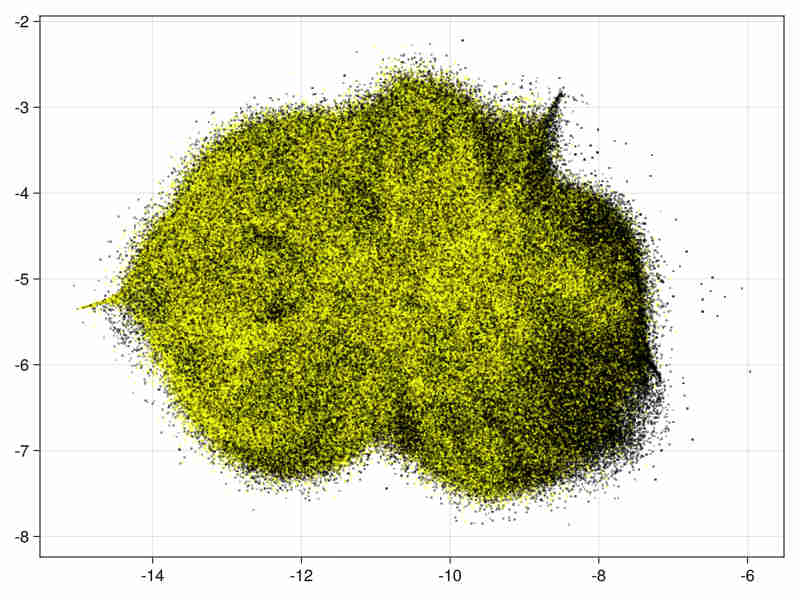
    higgs-28

    • 使用0.15的子采样因子进行质量评估

      在数据上使用0.15的子采样因子运行28变量（1.65百万数据点）在16分钟内完成

      无匹配的邻域数：869192，匹配时保留的邻居平均数：5.449e0

      因此，大约一半的邻域在嵌入中部分被尊重。

      关于比率的分位数：原始空间邻居在嵌入空间中的距离/嵌入空间中邻居的距离

      原始邻域的一半嵌入在嵌入图邻域半径的1.30倍内

      分位数在0.25：7.87e-2，0.5：1.30e0，0.75：4.75e0，0.85：7.94e0，0.95：1.62e1

      平均比率为：4.36

    28变量，子采样0.15

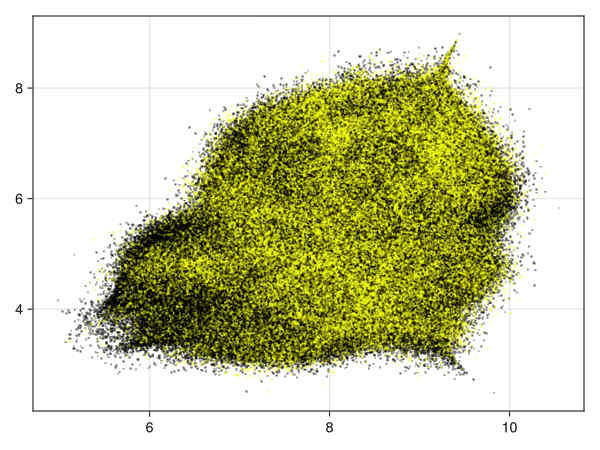
    higgs-28-subs0.15

    通过将距离转换为第一个邻居获得点的密度（参见visu.jl）

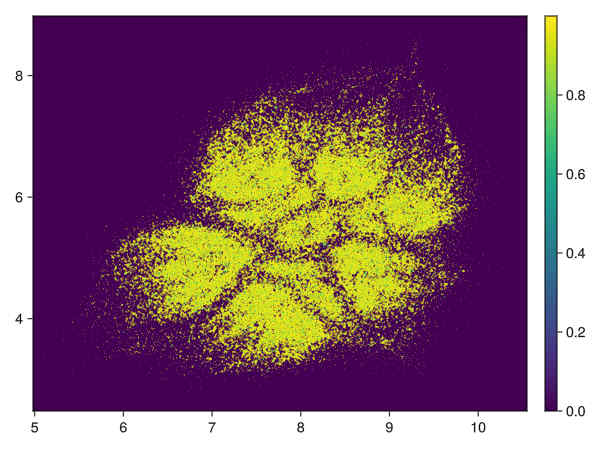
    higgs-28-density

    • 非分层情况下的扩散映射初始化。

      在直接情况下，近似SVD的初始扩散映射运行在1650秒，并产生以下初始化图像

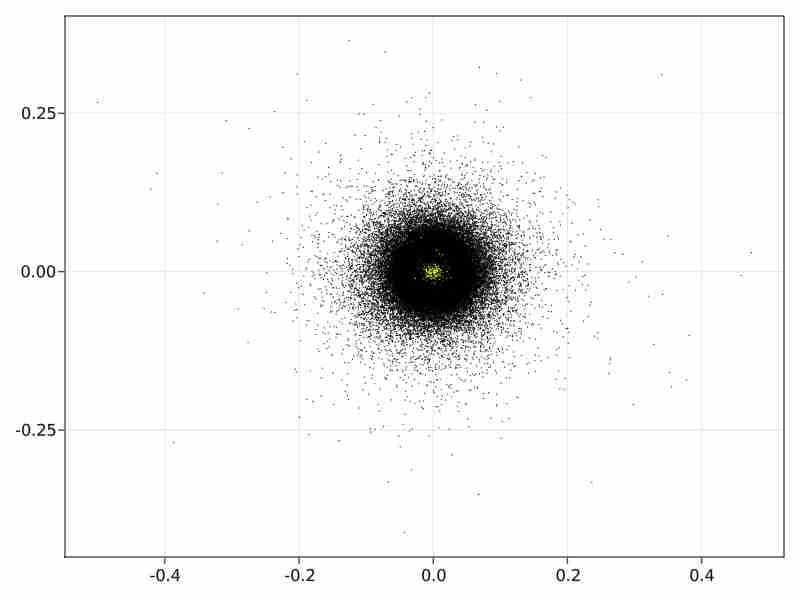
    higgs_dmap

用法

    // allocation of a Hnsw structure to store data
    let ef_c = 50;
    let max_nb_connection = 70;
    let nbimages = images_as_v.len();
    let nb_layer = 16.min((nbimages as f32).ln().trunc() as usize);
    let hnsw = Hnsw::<f32, DistL2>::new(max_nb_connection, nbimages, nb_layer, ef_c, DistL2{});
    let data_with_id : Vec<(&Vec<f32>, usize)>= images_as_v.iter().zip(0..images_as_v.len()).collect();
    // data insertion in the hnsw structure
    hnsw.parallel_insert(&data_with_id);
    // choice of embedding parameters 
    let mut embed_params = EmbedderParams::new();
    embed_params.nb_grad_batch = 15;
    embed_params.scale_rho = 1.;
    embed_params.beta = 1.;
    embed_params.grad_step = 1.;
    embed_params.nb_sampling_by_edge = 10;
    embed_params.dmap_init = true;
    // conversion of the hnsw to a graph structure
    let knbn = 8;
    let kgraph = kgraph_from_hnsw_all(&hnsw, knbn).unwrap();
    // allocation of the embedder and embedding
    embedder = Embedder::new(&kgraph, embed_params);
    let embed_res = embedder.embed();

随机化SVD

随机化SVD基于Halko-Tropp的论文。该实现涵盖了密集矩阵或如sprs crate提供的压缩行存储的矩阵。

用于近似SVD的两种范围逼近算法是

  • subspace_iteration_csr ，对应于Tropp论文中的算法4.4。它使用QR稳定化。

  • adaptative_range_finder_matrep 对应于Tropp论文中的算法4.2。该算法不如subspace_iteration_csr精确，但可以处理更大的矩阵，例如有百万行行的稀疏矩阵。

参考文献

  • 使用t_sne可视化数据。Van der Maaten和Hinton 2008。

  • 可视化大规模高维数据。Tang Liu WWW2016 2016 LargeVis

  • Phate：用于生物数据探索的结构和转换可视化。K.R Moon 2017。

  • Umap：降维中的均匀流形逼近和投影。L.MacInnes，J.Healy和J.Melville 2018

  • 随机聚类嵌入。Zhirong Yang，Yuwei Chen，Denis Sedov，Samuel Kaski，Jukka Corander。
    统计学和计算2023。 SCE

许可

许可方式为以下之一

  1. Apache许可证，版本2.0，LICENSE-APACHE 或 http://www.apache.org/licenses/LICENSE-2.0

  2. MIT许可证 LICENSE-MIT 或 http://opensource.org/licenses/MIT

根据您的选择。

依赖项

~79–110MB
~1.5M SLoC