3个版本
| 0.1.3 | 2024年2月24日 |
|---|---|
| 0.1.1 | 2023年10月10日 |
| 0.1.0 | 2023年10月10日 |
#648 in 算法
每月 30 次下载
170KB
455 行
Whittaker-Eilers平滑和插值
Whittaker-Eilers平滑器是完美的平滑器。它提供极其快速、高效的平滑,并通过每个测量的权重实现内置插值。此crate提供稀疏矩阵实现,以提高速度和内存效率,并且可以处理等间距和不等间距的测量。
[dependencies]
whittaker-eilers = "0.1.3"
使用方法
要开始平滑和插值数据,请通过new函数创建可重用的WhittakerSmoother结构体。如果您的数据长度或采样率发生变化,则需要重新创建此结构体。
等间距数据
这是最快的平滑选项。它使用两个可调参数(2e4的lambda和2的平滑器阶数)平滑等间距的y测量值。lambda越大,数据越平滑。
use whittaker_eilers::WhittakerSmoother;
let data_to_smooth = vec![1.1, 1.9, 3.1, 3.91, 5.0, 6.02, 7.01, 7.7, 9.0, 10.0];
let whittaker_smoother =
WhittakerSmoother::new(2e4, 2, data_to_smooth.len(), None, None)
.unwrap();
let smoothed_data = whittaker_smoother.smooth(&data_to_smooth).unwrap();
println!("Smoothed data: {:?}", smoothed_data);
非等间距数据
如果您希望平滑非等间距数据,则需要提供一个包含样本时间/位置的x_input。
use whittaker_eilers::WhittakerSmoother;
let x_input = vec![1.1, 1.9, 3.1, 3.91, 5.0, 6.02, 7.01, 7.7, 9.0, 10.0];
let data_to_smooth = vec![1.1, 1.9, 3.1, 3.91, 5.0, 6.02, 7.01, 7.7, 9.0, 10.0];
let whittaker_smoother =
WhittakerSmoother::new(2e4, 2, data_to_smooth.len(), Some(&x_input), None)
.unwrap();
let smoothed_data = whittaker_smoother.smooth(&data_to_smooth).unwrap();
println!("Smoothed data: {:?}", smoothed_data);
加权和插值
然后可以为每个测量值设置权重,以更信任某些测量值。将测量值的weights设置为0将导致插值。
use whittaker_eilers::WhittakerSmoother;
let x_input = vec![1.1, 1.9, 3.1, 3.91, 5.0, 6.02, 7.01, 7.7, 9.0, 10.0];
let data_to_smooth = vec![1.1, 1.9, 3.1, 3.91, 5.0, 6.02, 7.01, 7.7, 9.0, 10.0];
let mut weights = vec![1.0; x_input.len()];
weights[5] = 0.0;
let whittaker_smoother =
WhittakerSmoother::new(2e4, 2, data_to_smooth.len(), Some(&x_input), Some(&weights))
.unwrap();
let smoothed_data = whittaker_smoother.smooth(&data_to_smooth).unwrap();
println!("Smoothed data: {:?}", smoothed_data);
使用交叉验证进行平滑
使用此包,您还可以计算平滑系列的同时进行交叉验证错误。尽管如此,在生产环境中通常不应使用此功能,因为速度是必需的!
use whittaker_eilers::WhittakerSmoother;
let x_input = vec![1.1, 1.9, 3.1, 3.91, 5.0, 6.02, 7.01, 7.7, 9.0, 10.0 ,11.0, 12.0, 13.0];
let data_to_smooth = vec![1.1, 1.9, 3.1, 3.91, 5.0, 6.02, 7.01, 7.7, 9.0, 10.0, 11.0, 12.0, 13.0];
let whittaker_smoother =
WhittakerSmoother::new(2e4, 2, data_to_smooth.len(), Some(&x_input), None)
.unwrap();
let smoothed_and_cross_validated = whittaker_smoother.smooth_and_cross_validate(&data_to_smooth).unwrap();
println!("Result: {:?}", smoothed_and_cross_validated);
自动平滑
平滑数据需要选择Lambda。这可以通过视觉检查或找到导致最低交叉验证错误的lambda来完成。smooth_optimal函数运行各种lambda的平滑器,并返回具有检索最优结果的能力的结果。
use whittaker_eilers::WhittakerSmoother;
let x_input = vec![1.1, 1.9, 3.1, 3.91, 5.0, 6.02, 7.01, 7.7, 9.0, 10.0 ,11.0, 12.0, 13.0];
let data_to_smooth = vec![1.1, 1.9, 3.1, 3.91, 5.0, 6.02, 7.01, 7.7, 9.0, 10.0, 11.0, 12.0, 13.0];
let mut whittaker_smoother =
WhittakerSmoother::new(2e4, 2, data_to_smooth.len(), Some(&x_input), None)
.unwrap();
let results = whittaker_smoother.smooth_optimal(&data_to_smooth, true).unwrap();
println!("Result: {:?}", results);
println!("Optimal result: {:?}", results.get_optimal());
您可以将这些方法组合起来使用,例如,在不提供x输入的情况下进行插值测量。有关更高级的用法示例,请参阅Github仓库中的示例、测试和bench。以下是来自示例中一些平滑数据的图片。
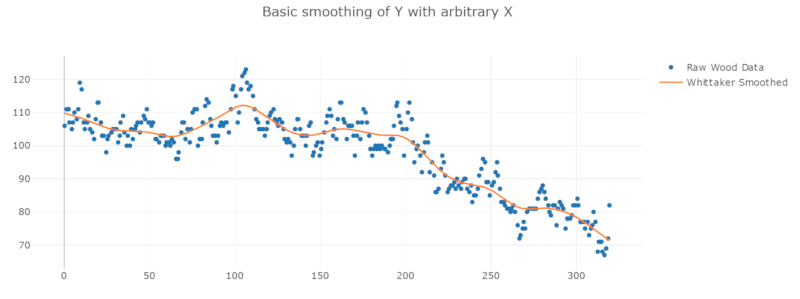
进一步阅读
如果您想更详细地了解这个库,请查看这篇Medium帖子。在其中,我对与其他平滑方法的示例和基准进行了分析。
未来功能
- 散点图平滑
- 泛型类型
参考文献
此处实现的算法与Paul H. C. Eilers在2003年Matlab中实现的版本类似。我在此crate的测试中包含了原始论文中的脚本和数据。原始论文和代码可以在以下地址找到
完美的平滑器 Paul H. C. Eilers 分析化学 2003 75 (14), 3631-3636 DOI: 10.1021/ac034173t
依赖项
~5MB
~102K SLoC