6 个版本 (3 个稳定版)
| 1.0.2 | 2024 年 2 月 7 日 |
|---|---|
| 1.0.1 | 2023 年 12 月 12 日 |
| 1.0.0 | 2023 年 11 月 16 日 |
| 0.1.2 | 2021 年 9 月 20 日 |
#30 在 数学 中
每月 22,814 次下载
用于 4 crates
45KB
770 代码行
simple_moving_average
本库提供了一系列计算一系列数据样本简单移动平均(SMA)的算法。SMA 通常用于实现低通滤波器,这是第二有用的滤波器类型,仅次于咖啡过滤器。
所有算法都实现了 [SMA] 特性,该特性提供了一个与实现无关的接口。接口对样本类型是泛型的,这意味着任何支持加法和标量除法的类型都可以进行平均。这包括大多数原始数值类型(f32、u32、...)、Duration 以及许多第三方数学库(例如 nalgebra、euclid、cgmath、...)的向量和矩阵类型。
项目状态
该库正在积极使用,功能完整,经过全面测试,并且没有已知的错误。它可以被认为是生产就绪的,但因为它没有明显的需求来推动它,所以它没有被积极开发。欢迎通过 GitHub 提交错误报告、功能请求和拉取请求。
示例
标量
let mut ma = SumTreeSMA::<_, f32, 2>::new(); // Sample window size = 2
ma.add_sample(1.0);
ma.add_sample(2.0);
ma.add_sample(3.0);
assert_eq!(ma.get_average(), 2.5); // = (2 + 3) / 2
向量
let mut ma = NoSumSMA::<_, f64, 2>::new();
ma.add_sample(Vector3::new(1.0, 2.0, 3.0));
ma.add_sample(Vector3::new(-4.0, -2.0, -1.0));
assert_eq!(ma.get_average(), Vector3::new(-1.5, 0.0, 1.0));
持续时间
let mut ma = SingleSumSMA::<_, _, 10>::from_zero(Duration::ZERO);
loop {
let instant = Instant::now();
// [ application code ]
ma.add_sample(instant.elapsed());
dbg!("Average iteration duration: {}", ma.get_average());
# break;
}
算法实现
计算简单移动平均以获得良好性能的一种方法是将之前计算缓存起来,特别是当前样本窗口中样本的总和。缓存这个总和既有优点也有缺点,这正是下面提出的三种不同实现所激发的。
| 实现 | 添加样本 | 获取平均值 | 注意事项 |
|---|---|---|---|
| [NoSumSMA] | O(1) |
O(N) |
- |
| [SingleSumSMA] | O(1) |
O(1) |
累积浮点舍入误差。 |
| [SumTreeSMA] | O(日志(N)) |
O(1) |
- |
N 指的是样本窗口的大小。
所有实现都具有 O(N) 空间复杂度。[NoSumSMA] 和 [SingleSumSMA] 完全由数组支持,因此默认情况下是堆分配的。[SumTreeSMA] 在数组中存储一些数据,但其和树存储在 Vec 中。
NoSumSMA
实现移动平均最直接的方法是不缓存任何总和,因此该实现的名称。所有样本的总和从头开始计算,时间复杂度为 O(N)(其中 N 为样本窗口大小),每次请求平均值时都会重新计算。
何时使用
- 当样本窗口大小非常小,样本求和成本可以忽略时。
- 当新样本写入的频率远高于读取平均值时。
SingleSumSMA
这种实现将样本窗口中所有样本的总和缓存为一个单独的值,因此读写新样本和读取其平均值的时间复杂度都为 O(1)。这种方法的缺点是,大多数浮点数无法精确存储,因此每次将此类数值添加到缓存的总和中,都有积累舍入误差的风险。
累积误差的大小取决于许多因素,包括样本窗口大小和样本分布。以下是 [SingleSumSMA] 和 [NoSumSMA](不遭受累积舍入误差)之间平均值的绝对差异随样本数量增加的可视化,对于典型窗口大小和一组样本。
Sample type: f32,Sample window size: 10,Sample distribution: Uniform[-100, 100]
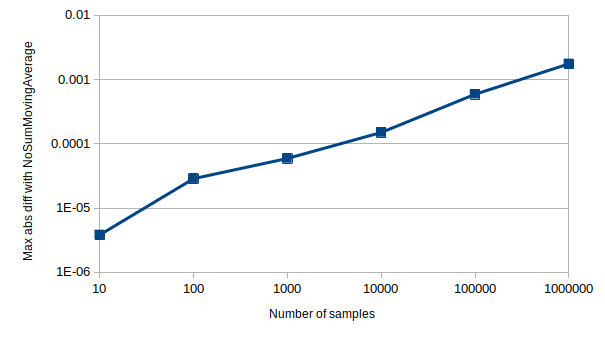
注意: 图表的两个轴都是对数刻度。Y 轴值表示 100 次测试运行中找到的最大差异。
减少误差的一种方法是将类型改为更宽的类型,例如使用 f64 而不是 f32。当样本位于区间 [-1, 1] 时,绝对误差也较小,因为这是浮点精度最高的地方。
何时使用
SumTreeSMA
有一种避免累积浮点舍入误差的方法,而不必每次请求平均值时都重新计算整个样本总和。然而,这种方法涉及数学和二叉树
总和是将二进制和 结合律 加法运算应用于一组操作数的结果,这意味着它可以表示为总和的二叉树。
例如
(1) + (2) + (3) + (4) + (5) + (6) =
(1 + 2) + (3 + 4) + (5 + 6) =
(3) + (7) + (11) =
(3 + 7) + (11) =
(10) + (11) =
(10 + 11) =
(21)
可以表示为以下树。
21
/ \
/ \
10 11
/ \ \
/ \ \
3 7 11
/ \ / \ / \
1 2 3 4 5 6
如果一个叶节点(即样本)发生变化,则只需重新计算该叶节点与根节点之间的直接路径上的节点,从而仅需进行 log(N) 次计算,其中 N 是窗口大小。这正是添加样本时发生的情况;最老的样本被新的样本替换,并且对应于最老样本的树叶节点使用新的样本值更新。
在更新某个叶节点的邻居时,始终会重新读取一个现有的叶节点(即样本值),这意味着在添加 N 个样本之后,所有叶节点都已被重新读取。这正是防止浮点数舍入误差累积的原因。
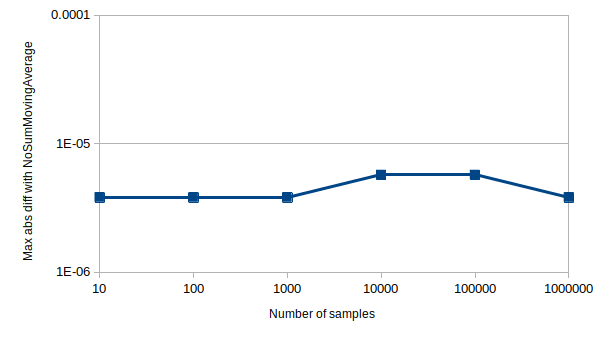
作者注: 如果有人愿意并且有头脑来正式证明这一点,他们非常欢迎提交一个 PR。在此期间,有一个单元测试从经验上证明了舍入误差不会累积。该测试的输出数据部分在下面的图表中进行了可视化,显示与 [NoSumSMA] 相比没有累积的舍入误差。
何时使用
- 在涉及浮点数据的大多数情况下,除非写入比读取更常见。
许可证
MIT
依赖项
~155KB