4 个版本
| 0.2.1 | 2023年11月2日 |
|---|---|
| 0.2.0 | 2023年11月2日 |
| 0.1.1 | 2023年10月26日 |
| 0.1.0 | 2023年10月26日 |
#421 在 算法
每月 21 次下载
36KB
553 行
rand-sequence (已弃用,推荐使用 rand-unique)
请注意,此 crate 已更名为 rand-unique,更能描述此 crate 的功能。如果您想获得 rand-sequence crate 命名的所有权,请 在 GitHub 上提出问题。
确定性地生成一个唯一的随机数序列。一个非重复的伪随机数生成器,可以直接索引序列中的第 n 个数字。
不提供加密安全。复杂性:所有操作的时间复杂度和空间复杂度均为 O(1)。
属性
- 序列是确定性的,对于相同的种子可以重复。
- 序列中只包含每个数字一次(每个索引都有唯一的输出)。
- 序列是伪均匀分布的。
- 尚未出现在序列中的每个数字都有大约相同的概率成为序列中的下一个数字。
- 请注意,一旦数字出现在序列中,它将不再出现。序列中的每个值都是唯一的。
- 计算序列中任何随机索引的值是一个 O(1) 操作。
RandomSequence::n(index)返回序列给定位置的输出。
- 支持
u8、u16、u32、u64和usize。输出可以分别转换为i8、i16、i32、i64和isize。
特性
此 crate 与 no-std 兼容。
default-features:randrand:启用在RandomSequenceBuilder和RandomSequence上的辅助方法rand(&mut RngCore),以随机种子初始化,这需要rand依赖项。可以省略,而是手动为RandomSequenceBuilder::seed()方法提供种子以实例化。serde:启用RandomSequenceBuilder的serdeSerialize和Deserialize支持,这需要serde依赖项。
示例
use rand::rngs::OsRng;
use rand_sequence::{RandomSequence, RandomSequenceBuilder};
// Initialise a sequence from a random seed.
let config = RandomSequenceBuilder::<u64>::rand(&mut OsRng);
let mut sequence = config.into_iter();
// Iterate over the sequence with next() and prev(), or index directly with n(i).
assert_eq!(sequence.next().unwrap(), sequence.n(0));
assert_eq!(sequence.next().unwrap(), sequence.n(1));
assert_eq!(sequence.next().unwrap(), sequence.n(2));
// Unique across the entire type, with support for u8, u16, u32, and u64.
let sequence = RandomSequence::<u16>::rand(&mut OsRng);
let nums: std::collections::HashSet<u16> = (0..=u16::MAX)
.into_iter()
.map(|i| sequence.n(i))
.collect();
assert_eq!(nums.len(), u16::MAX as usize + 1);
// Serialise the config to reproduce the same sequence later. Requires the
// "serde" feature to be enabled.
// let config = serde_json::to_string(&sequence.config).unwrap();
输出分布
未来的工作可能包括对输出分布的更严格分析。目前,以下图表显示了RandomSequence<u16>的大致均匀分布。
RandomSequence输出分布的直方图可视化。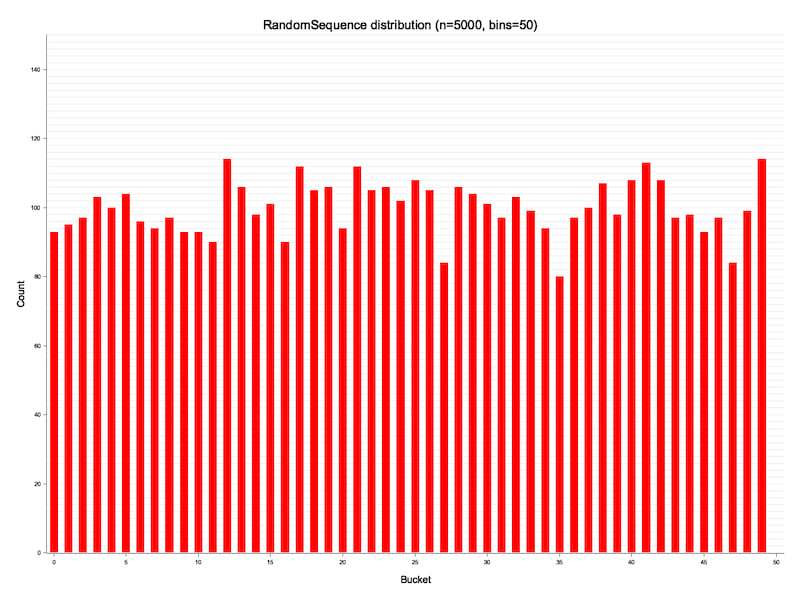
RandomSequence输出的散点图可视化。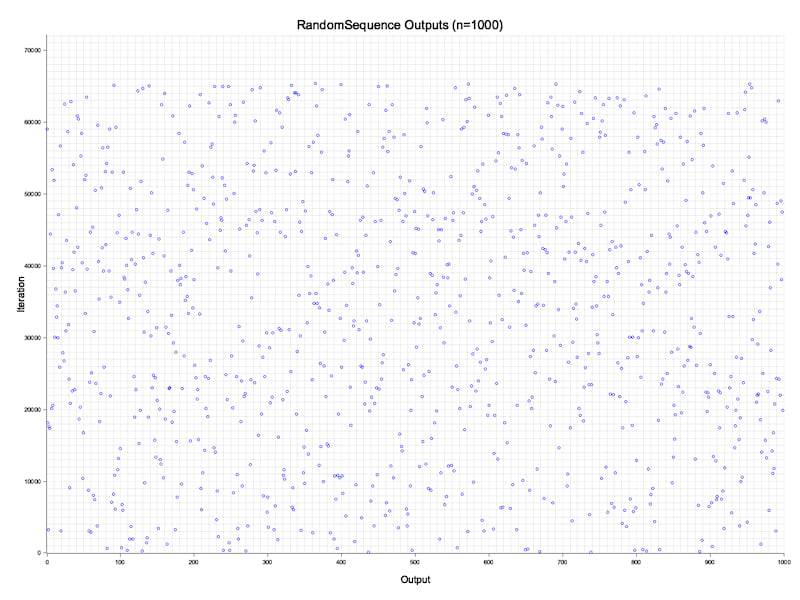
工作原理
这个非重复伪随机数生成器通过创建针对序列中的索引的排列函数(在此称为x)来工作。因此,对于序列中的任何位置x,我们希望通过函数n(x)确定性地计算一个唯一的输出数字,其中比较n(x)和n(x + 1)将看起来是随机生成的。
对于满足$p 3 \mod 4$的任何素数$p$,则对于任何输入$x$,操作$f(x) = x^2 \mod p$将为每个$x$值产生一个唯一的数字,其中$2x < p$。
二次剩余倾向于将数字聚集在一起,因此我们将二次剩余排列与其他排列函数(包装加法和异或)一起应用,以添加更多噪声。排列函数是那些对于所有输入到输出的直接1-1映射的函数,其中每个输入都有一个唯一的输出。
以简化的形式,排列函数是
/// `p` is chosen to be the largest number satisfying:
/// - a prime number
/// - that satisfies p = 3 mod 4 (`p % 4 == 3`)
/// - that fits in the datatype chosen, in this example `u64`
const PRIME: u64 = 18446744073709551427;
/// Simplified example of the quadratic residue function, taking input `x` for prime `PRIME`.
fn permute_qpr(x: u64) -> u64 {
// we choose x to be the largest prime number of the type, and so there are a small handful
// of numbers in the datatype which are larger than p. We map them directly to themselves.
if x > PRIME {
return x;
}
// compute the residue, in the real method we're careful to avoid integer overflow, omitted here
// for clarity.
let residue = (x * x) % PRIME;
// the residue is unique for all x <= p/2; and so p-residue is also unique for x > p/2.
if x <= PRIME / 2 {
residue
} else {
PRIME - residue
}
}
/// Randomly selected variables to introduce further noise in the output generation.
const OFFSET_NOISE: u64 = 0x46790905682f0161;
const XOR_NOISE: u64 = 0x5bf0363546790905;
/// We can then use this permutation function [permute_qpr] to build our number generator `n(x)`.
fn n(x: u64) -> u64 {
// function sequence: permute_qpr, wrapping addition, xor, permute_qpr
// care is taken in the real implementation to use wrapping addition, omitted here for clarity.
permute_qpr((permute_qpr(x) + OFFSET_NOISE) ^ XOR_NOISE)
}
来源
基于使用二次素数剩余的@preshing的文章
依赖项
~335–640KB
~12K SLoC