3个版本
| 0.1.2 | 2024年7月26日 |
|---|---|
| 0.1.1 | 2024年7月25日 |
| 0.1.0 | 2024年7月24日 |
#254 在 游戏开发
368 每月下载量
150KB
3K SLoC
一个用于二维约束Delaunay三角剖分的快速Rust库
示例
-
简单正方形上的Delaunay三角剖分
cd examples cargo run --example dt -
小图形上的约束Delaunay三角剖分
cd examples cargo run --example cdt -
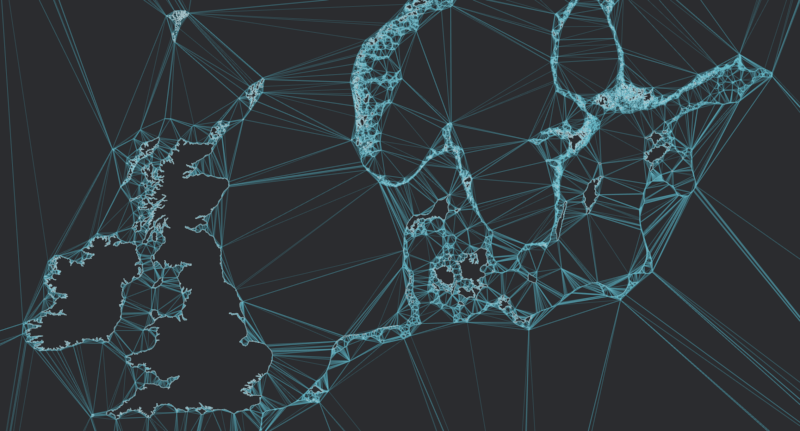
海岸线数据集上的约束Delaunay三角剖分
cd examples cargo run --release --example cdt_real_data示例源中指定了加载的数据集
- ne_50m_coastline: 60416个顶点,58987个约束边
- ne_10m_coastline: 410957个顶点,406824个约束边
- Europe_coastline: 2912812个顶点,2837094个约束边
-
视频"Bad Apple"上的约束Delaunay三角剖分
cd examples cargo run --release --example bad_apple示例源中指定了加载的帧。帧数据使用自定义工具生成。
在此处查看完整视频的结果:https://www.youtube.com/watch?v=TrfDkD_PprQ
所有示例都使用Bevy来可视化并探索生成的三角剖分。
附加示例资产
由于大小原因,示例中使用的某些资产没有直接包含在存储库中,但存储在git子模块assets/heavy中。
要下载它们,只需使用以下命令拉取子模块
git submodule update --init --recursive
基准测试
查看基准测试
实现
实现基于S. W. Sloan的《快速生成约束Delaunay三角剖分算法》(1993)。之所以选择它,是因为从DT(Delaunay三角剖分)到CDT(约束Delaunay三角剖分)的路径似乎相当直接。但是对原始算法做了一些修改。
一些定义,用于阐明说明
- 超级三角形:首先插入到三角剖分中的人工三角形,假定包含要三角剖分的所有顶点(*),在返回三角剖分结果之前被删除。
- 无限三角形:超级三角形的演变,具有位于无限位置的症状顶点。
- 无限四边形:无限三角形的演变,具有4个无限顶点。
- 超级/无限顶点:超级/无限三角形的一个顶点。
- 伪超级/无限三角形:其3个顶点中至少有一个超级/无限顶点的三角形。
- 有限顶点:算法输入的任何顶点。
- 半无限边:一个有限顶点和一个无限顶点构成的边。
- 无限边:两个无限顶点构成的边。
- 四边形:共享公共边的三角形对。
(*) 为了更准确,它应包含三角剖分中所有可能三角形的所有可能的圆。
修改
1- 重复和共线顶点
- 为了避免一些浮点精度问题,合并重复顶点或彼此之间非常接近的顶点(最终三角剖分中只会出现一个)
- 为了避免在三角剖分过程中创建扁平三角形,在三角剖分中插入顶点时,如果它位于已存在三角形的边(或非常接近它),而不是将包围三角形分割成3个,则将现有三角形分割成2个,其相邻的(共享边的)也分割成2个。然后对4个创建的四边形执行delaunay修复步骤(而不是“正常”情况下的3个)。
2- 无限“超级”顶点
为了正确处理“超级三角形”属性,进行了更复杂的修改。
考虑到它应包含三角剖分中所有可能三角形的所有可能的圆,我们不能简单地将其顶点取为有限值,即使是根据输入数据计算出的非常大的值。事实上,观察一个几乎平的三角形,其外接圆可以有一个几乎无限的半径,因此,如果超级顶点具有有限坐标,它可能包含在这个圆内。
为了避免在Delaunay修复阶段发生错误的对角线交换(和遗漏的对角线交换),超级顶点应被视为不同。
一些讨论和实现尝试修复Bowyer-Watson算法中的此缺陷,例如
- Stack Overflow讨论 和一个 Mathematics Stack Exchange讨论。
- chriszski用C++实现的 DT实现,OskarSigvardsson用C#实现的另一个 DT实现。
在Delaunay三角剖分中,根据前面链接中找到的想法,当面对伪无限三角形时,点在圆内测试变为点在半平面内测试(一个几乎无限的半径的圆可以局部近似为一条线)。此测试有两种变体
- 对于一个具有1个有限顶点的三角形:我们测试点相对于由两个有限顶点形成的线的位置。
- 对于一个具有2个有限顶点的三角形:我们测试点相对于通过有限顶点并具有两个无限顶点之间线斜率的线的位置。
但是,没有找到关于CDT的先前讨论,因此,为此部分实现的解决方案不是基于先前的工作,并且可能需要进行改进。如果您知道其他方法,请提交问题。
在约束Delaunay三角剖分中,除了重用无限外接圆测试之外,还有两个主要差异
- 当检查约束边与任何三角形边的交点时,必须考虑三角形边可能具有1个或2个无限顶点(然而,约束边始终是有限的,因为它连接两个有限顶点)。
- 无限边是平凡的,与约束边的交点是不可能的。
- 对于半无限边,我决定从有限顶点开始,沿着考虑的无限顶点的方向外推一个有限段。对于有限段长度,由于所有有限顶点都在单位正方形[0,1]中归一化,我简单地指定了一个略高于1.0的长度,以确保无论有限顶点的位置如何,都能覆盖整个单位正方形。
- 在检查四边形的对角线交点时,我们必须考虑到它们都可能都是半无限边。(四边形的对角线不能是无限边,因为不会有三角形共享这条边)。同样,对于约束边,我们从半无限边外推有限段并检查它们是否相交。
3- 无限顶点位置
在开发过程中,将无限顶点放置在X轴和Y轴上似乎很重要。当外推半无限边到有限边时(具有如 [(-inf,-inf), (0,+inf), (+inf,-inf)] 位置的无限三角形)时遇到了问题。
在将半无限边外推(由于超级三角形的形状,外推斜率 a != 0)时,一些三角形的绕行顺序最终被反转,并找到了错误的交点。然而,这可能是由于当时在 (find_vertex_placement) 中的错误。需要进行调查以查看/证明现在固定的实现是否还会出现同样的问题。
4- 无限四边形
当使用一个无限三角形,其在X轴(y=0)上有两个无限顶点,在Y轴上有一个无限顶点时,将顶点插入到三角剖分中通常会在三角剖分的底部/顶部(取决于Y轴无限顶点的位置)出现重叠的扁平三角形,这往往会使得整个三角剖分不正确/不稳定。
为了解决这个问题,我们不使用无限三角形,而使用无限四边形:[(-inf,0), (0,+inf), (+inf,0), (0,-inf)]。通过在Y轴上添加另一个无限顶点,并将第一个插入步骤改为“四边形分割”(创建4个三角形)而不是“三角形分割”,我们完全消除了这个问题。
潜在改进
点定位算法 (find_vertex_placement)
这是找到在三角剖分中要插入的点的三角形/边的算法。它目前基于一种类似跳转和行走算法。
在查看当前三角形的边/邻居时,它目前没有使用启发式方法(如插入点到点的距离),而只是检查插入点位于边的哪一侧。为了防止一些浮点数不精确(例如,当插入点与当前评估的边共线时),添加了一个检查以确保我们不会在两个三角形之间循环。
在某些情况下添加启发式算法可能可以改善性能(?)并可能消除循环检查(但需要计算启发式算法)。需要测试和性能分析。
在约束Delaunay重建(restore_delaunay_triangulation_constrained)中交换历史记录
在CDT算法中重建Delaunay三角形的状 态时,通过迭代构建执行交换的集合来避免反复交换相同的对角线。理想情况下,我们希望防止这些循环而不是检测它们,但这似乎比看起来要困难。仅仅在圆周测试上稍微严格一些,就会在某些数据集上引起问题。
无限顶点位置
调查是否可能返回到配置为三角形的配置而不是四边形,配置为[(-inf,-inf), (0,+inf), (+inf,-inf)]而不是四边形,而不破坏CDT半无限边的外推。如果可能的话,不会产生任何性能改进,但会去除一个可能的不必要的特性。
杂项
基于性能分析数据实现了显著的优化
- 默认情况下,通过u32对顶点和三角形索引进行压缩(u64作为功能可用)。对于更小的数据集使用u16没有带来显著的好处。
- 将
Neighbor(可选三角形ID)类型压缩以适应自定义的u32/u64。 - 默认使用
f32顶点位置(f64作为功能可用)。在基准测试中使用的是f64。 - 大多数向量/堆栈在算法的迭代之间预分配和共享。
- 热函数内联(圆周测试等)。
- 在binsort阶段,可以配置bins中顶点的密度作为输入。略微增加它对于非局部顶点数据集(局部顶点→输入集合中的相邻顶点在空间上接近)会给出更好的结果。
- 仅对DT,并且当三角形数量足够大时,可以在并行中执行伪无限三角形的删除。尽管这并不是三角剖分中最关键的性能部分,但这仍然带来了一些可衡量的改进。
扫描线/圆
可能可以通过使用不同的算法来更快地实现CDT。在这个存储库中没有尝试过。这也可能使代码复杂度更简单,因为处理无限顶点确实给Sloan的算法增加了很多复杂性。
为什么是“ghx”?
- 它用作命名空间,以避免选择诸如
delaunay_triangulation之类的货物名称。
Glam版本
此存储库允许使用一系列的glam版本。如果您发现自己处于这种情况:cargo为ghx_constrained_delaunay拉取了一个新的glam版本,但您宁愿使用较旧的版本,您可以通过编辑您的cargo.lock文件来使用较旧的版本,或者使用以下命令:cargo update --package glam@NEWER_VERSION --precise VERSION_TO_USE
许可
代码
此存储库中的所有代码都根据以下任一许可进行双重许可:
- MIT许可(《LICENSE-MIT》或https://open-source.org.cn/licenses/MIT)
- Apache License,版本2.0(LICENSE-APACHE 或 https://apache.ac.cn/licenses/LICENSE-2.0)
除非您明确声明,否则根据Apache-2.0许可定义,您有意提交的任何贡献,包括您的工作,将按上述方式双许可,不附加任何额外条款或条件。
依赖项
~6MB
~140K SLoC