以简洁性为理念的图库。

Prepona旨在使用起来简单（对于库的用户）并进一步开发（对于贡献者）。几乎所有函数都有规格说明和示例，供用户快速了解如何使用特定功能。同时，几乎所有实现都有一个关于“为什么”以这种方式实现的注释，以便贡献者可以快速阅读代码，并专注于他们想要进行的改进。

总体结构

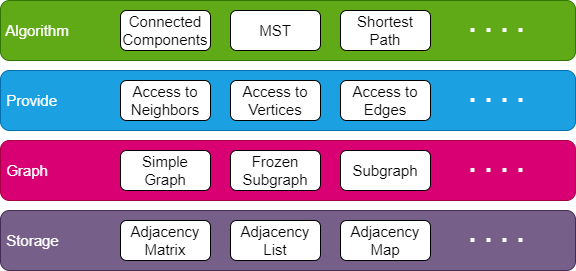
Prepona使用分层架构来表示其不同组件之间的逻辑关系。每一层都向其上层暴露功能。从下到上

• 存储：这一层包含不同的结构，可以存储有关图的信息。每个存储都必须实现GraphStorage特质。这使得更换存储为另一种存储变得轻而易举。此外，GraphStorage为其大多数函数提供了默认实现，因此您可以快速提供自定义实现，并逐步覆盖这些默认实现以实现具有更高性能的自定义实现。
• 图：这一层添加了更多逻辑，并位于存储之上。一个很好的例子是SimpleGraph结构，它可以防止在两个顶点之间添加环和多个边。将此逻辑与存储解耦使得可以使用存储来处理任何类型的图。
• 提供：这一层包含多个特质，每个特质都描述了一组由图公开的功能。例如，当一个图实现了Edges特质时，这意味着图提供了允许用户在图的边上进行计算的功能。
• 算法：本层包含可以在不同类型的图上执行的所有算法。请注意，算法不依赖于图结构。它们依赖于在提供层中定义的特性。这使得能够编写一个通用的（在这个意义上，算法不依赖于任何结构，而只依赖于结构提供的功能）算法，该算法可以在实现所需特性的任何类型的图上执行。例如，TopologicalSort 算法需要 Vertices 和 Neighbors 特性来完成其计算。因此，任何提供这两个特性的图、子图、增强图等，都是适合在 TopologicalSort 算法上执行的结构。

这种架构旨在简化该项目的使用和贡献。用户可以轻松尝试每种存储和图，无需对代码库进行很大改动。他们可以轻松地将默认值替换为自己的存储、图和算法。贡献者可以选择感兴趣的领域并改进该领域，而无需担心其他部分与他们的新增强兼容。

有关每个存储、图等的更多信息，请参阅项目的文档。

基本用法

首先，您必须选择一个要使用的存储。在本节中，我们将使用 AdjMatrix。

use prepona::prelude::*;
use prepona::storage::AdjMatrix;

let adj_matrix = AdjMatrix::<usize, DefaultEdge<usize>, UndirectedEdge>::init(); 

如您所见，有三个泛型参数必须指定。第一个参数确定将要存储的权重类型。如您所见，我们将其设置为 usize，因为我们想使边具有 usize 类型的权重。第二个参数确定将要存储的边的类型。我们在此示例中使用 DefaultEdge。 DefaultEdge 只有一个权重。但您可以定义自定义边类型。一个好的例子是 FlowEdge，它包含权重、容量和流量。最后，最后一个参数确定边是 DirectedEdge 还是 UndirectedEdge。我们现在选择无向边。这个声明太长了，所以 Prepona 提供了一些别名，使初始化存储的过程更容易、更易读。有关 AdjMatrix 所公开的所有别名，请访问其文档页面。现在我们使用与我们的定义 adj_matrix 兼容的一个。

use prepona::storage::Mat;

let adj_matrix = Mat::<usize>::init();

接下来，我们必须找到一个适合我们目的的图。在此示例中，我们将使用 SimpleGraph，因为我们不想在两个顶点之间有循环或多个边。

use prepona::graph::SimpleGraph;

// Initialize the graph with the storage you have chosen.
let mut graph = SimpleGraph::init(adj_matrix);

然后我们可以用顶点和边来填充我们的图

//                c    
//                   
//      a     b       d     e
//
let a = graph.add_vertex();
let b = graph.add_vertex();
let c = graph.add_vertex();
let d = graph.add_vertex();
let e = graph.add_vertex();

//            .-- c --.
//            |       |
//      a --- b ----- d --- e
//
let ab = graph.add_edge_unchecked(a, b, 1.into());
let bc = graph.add_edge_unchecked(b, c, 1.into());
let cd = graph.add_edge_unchecked(c, d, 1.into());
let bd = graph.add_edge_unchecked(b, d, 1.into());
let de = graph.add_edge_unchecked(d, e, 1.into());

如您所见，我们使用 add_vertex 为图添加新顶点，并将顶点返回的id存储在变量中。然后，我们使用 add_edge_unchecked 添加边（每条边的权重都等于1），并将边id存储在其各自的变量中。在Prepona中，任何可能有失败机会的函数都必须提供两个版本的自己：一个检查版和一个未检查版。在检查版中，在进行实际计算之前，将进行一些查找，以确保计算可行。如果图的当前状态和传递的参数没有问题，函数的检查版将返回包含计算结果的 Ok。但如果计算可能失败，检查版将返回一个带有解释错误的 Err。但未检查版可能会因为某些错误而崩溃。使用哪个版本由您决定。如果您确定您的图状态和传递给结构的参数，则使用未检查版以跳过查找并获得更好的性能。但如果您从可能产生有效数据源的值中读取，请使用检查版以防止代码中的崩溃。

现在我们可以在我们的图上执行算法。在这个例子中，我们假设这个图代表一个网络，我们想要找到那些如果删除，会导致我们的网络拓扑断开的顶点（连接节点）和边（链接）。

use prepona::algo::VertexEdgeCut;

let (cut_vertices, cut_edges) = VertexEdgeCut::init(&graph).execute(&graph);

// We find that vertices b and d are weak points in our topology. 
// And if any of them goes down, we will lose connection to part of our network topology.
assert!(
    vec![b, d]
    .iter()
    .all(|vertex_id| cut_vertices.contains(vertex_id))
);

// We find that links a -> b and d -> e are weak links in our topology. 
// And if any of them goes down, we will lose connection to part of our network topology.
assert!(
    vec![ab, de]
    .into_iter()
    .all(|edge_id| cut_edges.iter().find(|(_, _, edge)| edge.get_id() == edge_id).is_some())
);

然后，您可以使用这些信息来改变拓扑，以删除这些弱点/链接。

其他图库

还可以查看这些库

• petgraph
• graphlib

如果您知道其他库，请给我发电子邮件。我将很高兴在这里引用它们。

贡献

此项目使用与rust项目相同的行为准则。

尽量使用项目代码中已有的风格来记录您的代码。例如，如果您正在实现一个新算法，请确保简要说明该算法的作用，引用维基百科页面以获取有关算法的更多信息，列出参数并解释每个参数，解释返回值及其含义。最后，如果算法可能失败，返回一个Result，并尽可能避免panic。