Lib.rs

polysplit 库实现了允许通过定义的点列表将多边形线分割成段的算法。

下方的图像展示了其可视化效果，其中多边形线为蓝色，点列表为红色。虚线表示将点投影到分割多边形线的位置，粉色和蓝色区域表示段。

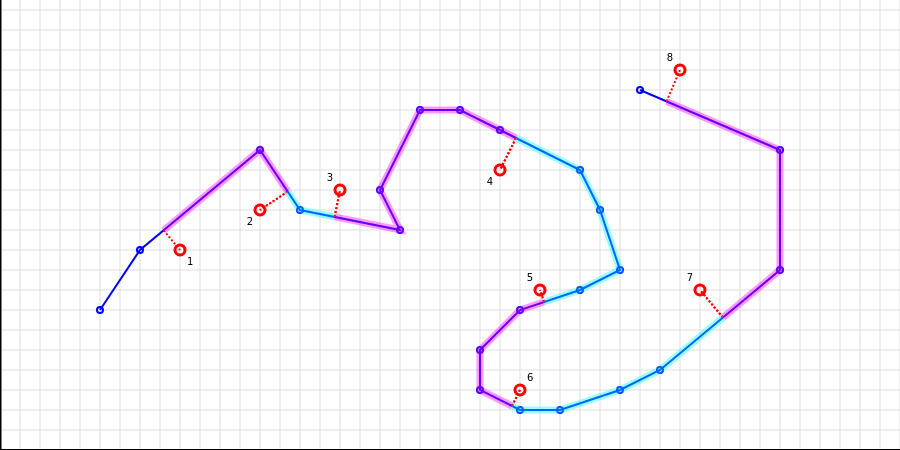
使用示例

use polysplit::polyline_split;
use polysplit::euclidean::Point;

fn main() {
    let polyline = vec![
        Point(0.0, 0.0),
        Point(3.0, 0.0),
        Point(7.0, 0.0),
        Point(10.0, 0.0),
        Point(13.0, 0.0),
        Point(17.0, 0.0),
        Point(20.0, 0.0)
    ];
    let split_points = vec![
        Point(1.0, 1.0),
        Point(19.0, 1.0)
    ];

    // Without minimum distance to polyline threshold
    let segments = polyline_split(&polyline, &split_points, None).unwrap();
    println!("{:?}", segments);

    // With minimum distance to polyline threshold
    let segments = polyline_split(&polyline, &split_points, Some(20.0)).unwrap();
    println!("{:?}", segments);
}

该算法考虑点的顺序，并保证段顺序的正确性。

它甚至允许在像下方的某些复杂情况下找到解决方案（检查点2、3和4、5的位置）

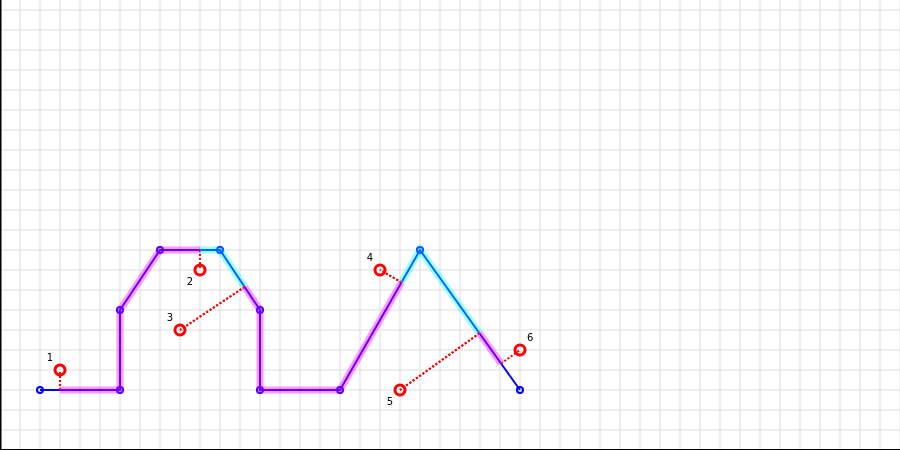
尽管点3更靠近多边形线的左侧部分，但最好将其投影到多边形线的右侧部分，以保证顺序正确。

另一个示例（点4、5和6、7）

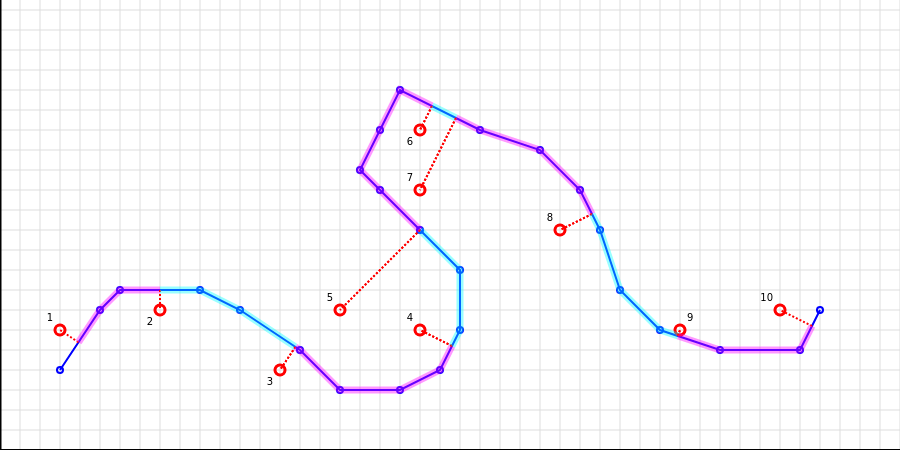
自定义类型

polysplit 提供了 euclidean 模块以供使用。但 polyline_split 可以用于您自己的数据类型。只需为所谓的“点”数据结构实现 PolySplit 特性即可。

trait PolySplit<D>
where
    Self: Copy,
    D: Copy + PartialOrd + Add<Output = D>,
{
    fn distance_to_point(&self, point: &Self) -> D;
    fn distance_to_segment(&self, segment: (&Self, &Self)) -> DistanceToSegmentResult<Self, D>;
}

例如，它可以是3D平面 Point(x, y, z)、地理 Location(经度, 纬度) 或球形 Point 投影。

其他使用

使用该算法还可以检查两条多边形线在一定距离阈值内是否相似。查看（polyequal）https://github.com/vchezganov/polyequal 库。