| 0.13.0 |
|
|---|---|
| 0.11.0 |
|
| 0.8.0 |
|
| 0.1.0 |
|
#4 in #kelvin
155KB
4K SLoC
Kelvin
一个Merkle树工具包和后端。
Merkle树和区块链
Merkle树允许开发人员以非常高效的方式将加密散列函数应用于状态的庞大表示。由于这个重要功能,Merkle树在各种去中心化应用中得到了广泛使用,在这些应用中,只有在网络节点能够确定整个系统的确切状态时,才能正确地实现独立实体的协调。在基于区块链的基础设施中,未使用的交易输出、链历史、账户状态和智能合约存储等都是大型状态表示的例子。
在编写涉及Merkle树的程序时,目前的做法是满足于一种基本的数据结构(例如,智能合约平台的一个流行选择是Patricia或Radix树)。
大多数实现都使用了键值数据库后端(RocksDB、LevelDB),这些后端针对可变数据的存储进行了优化(即可能被更新或删除的数据),因此,为了允许跟踪缓存失效和高效更新,它们具有不可忽视的额外开销。这种额外的逻辑在区块链用例中纯粹是一种不必要的复杂性,而区块链的本质是只追加存储不可变数据的存储。
另一个问题是大多数这些树实现与数据库后端的紧密耦合。这种做法的缺点是使这些实现缺乏灵活性,并依赖于特定数据库逻辑进行回滚和事务。因此,更改和/或实现替代数据结构不可避免地会导致复杂性和重复工作以及代码,因为每个新的树结构都需要自己的数据库集成层。理想情况下,在交易失败的情况下,你应该能够简单地丢弃失败状态,并从之前的状态继续,以非常低的额外开销。
为了解决这些问题,并允许更快的数据结构建模和迭代,我们引入了Kelvin!
动机
Kelvin是一个旨在结合不可变数据结构、磁盘持久性和内容寻址树(即Merkle树)优点的库。
在DUSK网络中,Kelvin已经成为一个不可或缺的工具,用于建模真正优化区块链数据结构,这些数据结构贯穿于许多需要状态表示的核心网络组件,从交易模型到智能合约引擎。Kelvin使我们能够避免为每个迭代单独实现存储和写时复制逻辑的繁琐工作。
数据结构逻辑与数据库后端管道、使用的哈希函数甚至元数据注释都分离。每个都可以单独优化和调整。
让我们先了解一下这三个主题的背景知识,然后再探讨它们是如何结合在一起的。
不可变数据结构
假设我们有一个这样的映射
{ a: 0, b: 1, c: 2, d: 3, e: 4 }
这可以用如下不可变数据结构表示
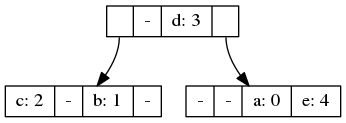
现在,假设我们将映射中的 e 设置为 42,结果的不变结构可能如下所示
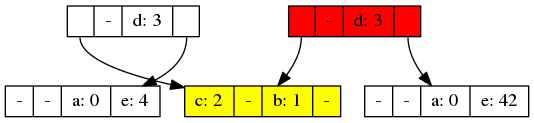
树的最左边的节点实际上是我们的旧映射,它没有改变!最右边的红色根节点是改变后的新映射。如您所见,两个映射在指向未改变的包含 b 和 c 的黄色节点方面共享结构。
这就是如何高效地保留旧映射的副本,您只需为实际改变的树部分支付存储和更新成本。
Clojure VS Rust
Clojure在推广不可变数据结构概念方面发挥了重要作用,Clojure的所有集合(映射/列表/集合)默认都是不可变的。尽管在实际情况下足够高效,但语言还支持所谓的transient数据结构。论点是,只要在修改期间没有其他线程可以看到结构,就可以使用更高效的非复制方法。如果您熟悉Rust,这可能会引起您的共鸣。
在Rust中,每个正在修改的数据结构已经是transient的,这基于 &mut 引用的保证。这意味着,我们得到了两者的最佳之处!
磁盘持久性
在程序中保存状态的最常见方式是通过文件系统,通常用于日志和配置文件,或者某种类型的数据库。
如果我们直接将我们的花哨树保存到磁盘上会怎样?如果您的程序状态可以表示为映射和集合的集合,为什么我们不能直接以它们当前的形式将它们写入磁盘呢?
让我们再次看看前面的例子,为什么根节点的子节点不能指向某种磁盘表示?并在需要时加载和缓存?这正是Kelvin的工作方式。
let mut state = ProgramState::new();
state.do_things_that_modify_state();
// Let's set up a store
let dir = tempdir().unwrap();
let store = Store::<Blake2b>::new(&dir.path());
// A snapshot is a hash and a reference to a Store
let snapshot = store.persist(&mut state).unwrap();
let mut restored = store.restore(&snapshot).unwrap();
// restored can now be used as a normal `ProgramState`
ProgramState本身可以是不同映射的任何组合,关于这一点我们稍后再谈。
内容可寻址性
内容可寻址是一种使用加密哈希来引用字节流的名称。在这种情况下,我们的ProgramState的序列化表示。这意味着,您用于查找数据的“键”就是该数据的表示。这有多个好处。
首先,您将获得免费的数据完整性检查,如果您通过其加密哈希查找已被修改或损坏的数据,您将立即注意到。您还可以获得去重。例如,如果您的状态包含多个等效的映射,如上面的示例中共享子树的情况,它将只在磁盘上存储一次。
Merkle树
Merkle树正是如此,根节点是其叶子或子树的哈希值的哈希。并且与Merkle树一样,Kelvin维护的结构也适合构建Merkle证明
自下而上的视图
那么,这是如何实现的,您需要如何调整您的程序状态以使用这个库?
内容特性
该库的主要特性是 Content 特性。它简单地定义了如何将特定类型转换为/从字节转换。
我们不使用 serde,因为我们想对类型施加额外的限制,例如使其 Clone:可克隆的、Eq 等等。我们还希望确保哈希值映射总是 1-1。
/// The main trait for content-adressable types, MUST assure a 1-1 mapping between
/// values of the type and hash digests.
pub trait Content<H: ByteHash>
where
Self: Sized + Clone + 'static + PartialEq + Eq,
{
/// Write the type to a `Sink`
fn persist(&mut self, sink: &mut Sink<H>) -> io::Result<()>;
/// Restore the type from a `Source`
fn restore(source: &mut Source<H>) -> io::Result<Self>;
}
这就是全部!只需为您的状态实现此类型,您就可以创建状态快照!
复合特性
复合特性用于创建您自己的数据结构。目前 kelvin 仅附带一个哈希数组映射 trie,这是 Clojure 为其映射使用的相同数据结构,但该库旨在尽可能简化您自己结构的实现。
/// A trait for tree-like structures containing leaves
pub trait Compound<H>: Content<H> + Default
where
H: ByteHash,
{
/// The leaf type of the compound structure
type Leaf: Content<H>;
/// Returns handles to the children of the node
fn children(&self) -> &[Handle<Self, H>];
/// Returns mutable handles to the children of the node
fn children_mut(&mut self) -> &mut [Handle<Self, H>];
}
实现 Compound 特性将为您提供访问 kelvin 的迭代器和搜索功能。您需要自己实现的功能只是 insert 和 remove 功能。目前 get、get_mut 等也需要手动实现,但这可能会改变。其余的由库处理。
处理类型
处理类型是树结构实现的核心。
pub struct Handle<C, H>(HandleInner<C, H>);
enum HandleInner<C, H>
where
C: Compound<H> [...]
{
Leaf(C::Leaf),
Node(Box<C>),
SharedNode(Arc<C>), // not yet implemented
Persisted(Snapshot<C, H>),
None,
}
每个处理可以是叶子、boxed 节点、共享节点、快照或 None。不同节点类型之间的区别隐藏在 Handle 类型之后,作为库的用户,您只需关注 Leaf、Node 和 None 的情况。
搜索
要搜索树,您使用 Method 特性,该特性由库在递归查找树中的分支时调用。
/// Trait for searching through tree structured data
pub trait Method: Clone {
/// Select among the handles of the node
fn select<C, H>(&mut self, handles: &[Handle<C, H>]) -> Option<usize>
where
C: Compound<H>,
H: ByteHash;
}
最简单的例子是找到树中的第一个非空节点。
impl Method for First {
fn select<C, H>(&mut self, handles: &[Handle<C, H>])
-> Option<usize> [...]
{
for (i, h) in handles.iter().enumerate() {
match h.handle_type() {
HandleType::Leaf | HandleType::Node
=> return Some(i),
HandleType::None => (),
}
}
None
}
}
这是在迭代树叶子时使用的默认方法。
对于在原始 HAMT 实现中找到正确的键槽,这是一个例子(实际实现更为优化)
fn calculate_slot(h: u64, depth: u64) -> usize {
let result = hash(depth + h);
(result % N_BUCKETS as u64) as usize
}
impl Method for HAMTSearch {
fn select<C, H>(&mut self, _: &[Handle<C, H>]) -> Option<usize>
{
let slot = calculate_slot(self.hash, self.depth);
self.depth += 1;
Some(slot)
}
}
关联树注释
可以用于搜索的树元数据,例如
基数,用于有效地找到集合的第 n 个元素
校验和,用于集合之间常量时间的相等性检查
最小/最大值,用于优先队列功能
这是基数注释的外观
#[derive(PartialEq, Eq, Clone)]
pub struct Cardinality<T>(T);
impl<T> Associative for Cardinality<T>
where
T: Counter,
{
fn op(&mut self, b: &Self) {
self.0 += b.0;
}
}
impl<Anything, U> From<&Anything> for Cardinality<U>
where
U: Counter,
{
fn from(_: &Anything) -> Self {
Cardinality(U::one())
}
}
From<&Anything> 的实现意味着,任何叶子都将被计为 1,并且随着子树注释的计算,使用简单的加法。
要合并多个注释为一个,请使用 annotation! 宏。以下是 BTree 实现的示例
annotation! {
pub struct BTreeAnnotation<K, U> {
key: MaxKey<K>,
count: Cardinality<U>,
}
where
K: MaxKeyType,
U: Counter
}
当使用此注释类型定义数据结构时,它将自动传播到根节点。
使用示例
以下是一个示例,说明您需要构建一个可持久化为 Merkle 树的程序状态。(来自 examples/simple)
use std::io;
use kelvin::{Blake2b, ByteHash, Content, Map, Root, Sink, Source};
use kelvin_btree::BTree;
#[derive(Clone)]
struct State<H: ByteHash> {
map_a: BTree<String, String, H>,
map_b: BTree<u64, u64, H>,
counter: u64,
}
// The initial root state
impl<H: ByteHash> Default for State<H> {
fn default() -> Self {
// Set up a default kv for map_a:
let mut map_a = BTree::new();
map_a
.insert("Hello".into(), "World".into())
.expect("in memory");
State {
map_a,
map_b: BTree::default(),
counter: 0,
}
}
}
impl<H: ByteHash> Content<H> for State<H> {
fn persist(&mut self, sink: &mut Sink<H>) -> io::Result<()> {
self.map_a.persist(sink)?;
self.map_b.persist(sink)?;
self.counter.persist(sink)
}
fn restore(source: &mut Source<H>) -> io::Result<Self> {
Ok(State {
map_a: BTree::restore(source)?,
map_b: BTree::restore(source)?,
counter: u64::restore(source)?,
})
}
}
fn main() -> io::Result<()> {
let mut root = Root::<_, Blake2b>::new("/tmp/kelvin-example")?;
let mut state: State<_> = root.restore()?;
match state.map_a.get(&"Foo".to_owned())? {
Some(path) => println!("Foo is {}", *path),
None => println!("Foo is `None`"),
}
println!("Counter is {}", state.counter);
state.counter += 1;
state.map_a.insert(
"Foo".into(),
format!("Bar {}", state.counter * state.counter),
)?;
root.set_root(&mut state)?;
Ok(())
}
待完成
这是一个测试版发布,我们不保证 API 的稳定性。一些功能尚未实现,但已设计。
垃圾回收
在 kelvin 中,垃圾回收将包括一个代复制收集器,给定一个根节点,从该节点可到达的所有内容都将复制到一个新的后端,并释放旧的一个。使用多个代使得平均速度快。
lib.rs:
在 kelvin 上实现的哈希数组映射 trie
依赖关系
~7–17MB
~239K SLoC