3 个版本
| 0.4.2 | 2019年4月29日 |
|---|---|
| 0.4.1 | 2019年4月29日 |
| 0.3.2 |
|
| 0.2.0 |
|
| 0.1.0 |
|
#15 in #neighbor
24 每月下载量
80KB
1.5K SLoC
hwt
来自论文《Hamming 空间中在线最近邻搜索》的 Hamming 权重树
要了解数据结构的工作原理,请参阅文档。
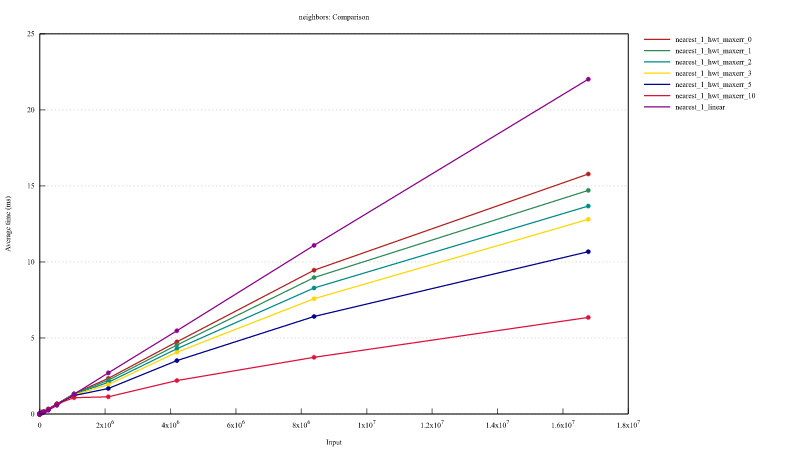
基准测试
1-NN 最新的基准测试
您可以在此处找到基准测试输出。
如果您想自己运行基准测试,只需在命令行中运行 cargo bench 即可。我建议使用 RUSTFLAGS='-C target-cpu=native' cargo bench,因为线性搜索和这个树在使用现代指令时都显著更快。
lib.rs:
Hwt
Hamming 权重树最初是在 Sepehr Eghbali、Hassan Ashtiani 和 Ladan Tahvildari 的论文“Hamming 空间中在线最近邻搜索”中实现的。这是尝试改进性能并将实现封装在 Rust crate 中以方便使用的一个尝试。
以下是我们可以如何从视觉上考虑一个数字,从其子串汉明权重二叉树的角度来看
5
3 2
2 1 1 1
1 1 0 1 1 0 0 1
让 B 是数字宽度的 log2。在这种情况下 B = 3,因为 2^3 = 8。
让 L 是汉明树的级别。整个数字的汉明权重是根,为 L = 0。
让 N 是 L 级别中子串权重的索引。
让 W 是 L 级别中子串 N 的权重。
设 MAX 为汉明树的一侧最大边。 MAX = min(W, 2^(B - L - 1))。这是子字符串两侧可以拥有的最大1的数量。
设 MIN 为汉明树的一侧最小边。 MIN = W - MAX。这是子字符串两侧可以拥有的最小1的数量。
每次我们在树中遇到权重 W 时,接下来的两个子字符串可以变化的范围从 [MIN, MAX] 到 [MAX, MIN],总共有 A + 1 种可能性。因此,我们也可以这样看待这棵树
5 [1-4] 2
3 2 [1-2] [0-2] 1 1
2 1 1 1 [1-1] [0-1] [0-1] [0-1] 0 0 1 0
1 1 0 1 1 0 0 1
左边是我们实际看到的树。中间是我们左分支的可能值。右边是我们选择的左分支的索引,这是通过从左子字符串权重中减去 MIN 来计算的。
为了计算 L 的索引,我们必须迭代地将累加器乘以当前子字符串 N 的 MAX - MIN + 1 倍,然后加上子字符串在树中的索引,然后将数字左移子字符串宽度位,得到 N + 1。
要执行反向操作,我们必须将累加器对所有下级子字符串的 MAX - MIN + 1 乘积进行模运算,以得到该子字符串的索引,然后除以当前子字符串的 MAX - MIN + 1。迭代执行以生成给定索引的所有权重。如果可能,我们应该避免在每次操作中多次从索引计算权重,因为这很耗时,因为涉及到模运算和除法。
搜索
为了限制搜索空间,我们依赖于这样一个事实:子字符串汉明权重的绝对差之和不能超过子字符串汉明距离之和。这意味着如果任何给定层树上桶索引的隐含权重的汉明权重绝对差之和超过 radius,则我们知道在那个树的分支中不可能找到任何结果。这允许我们只搜索理论上可能匹配的节点。
对于顶级,扫描(weight-radius..=weight+radius)是清晰的。这是因为结果无法在重量差异超过radius的地方找到。对于低于这个级别的级别,搜索桶变得更加复杂。为此,让我们考虑L = 0的情况(在查找整体汉明重量的桶之后开始第0级)。
假设我们有一个128位的特征,具有这样的汉明重量树
5
3 2
如果我们想搜索半径小于等于radius <= 1的东西,那么在顶级我们搜索4..6。让我们考虑当我们尝试搜索在索引4找到的桶时会发生什么。在这个时候,我们有一个左边可以在0..=4之间变化的情况,因为我们有一个128位数字,每个半部分可以轻松容纳4个1。然而,我们不需要搜索所有这些可能性。
如果左边有重量为1,则右边将有重量为3。记住“子字符串汉明重量的绝对差之和不能超过子字符串汉明距离之和。”如果我们看看我们的搜索点,我们会发现差值的总和是abs(3 - 1) + abs(2 - 3) = 3。这大于我们的搜索半径1,因此在那里找到汉明距离在半径内的数字是不可能的。
现在考虑如果我们把左边的重量提高到2会发生什么。在这种情况下,我们右边有2位。差值的总和是abs(3 - 2) + abs(2 - 2) = 1。这等于我们的搜索半径,因此可以在该桶中找到匹配项。
总之,我们需要在2..=3之间迭代。这大大限制了可能性。然而,我们需要知道如何推导这个范围。
我们要找的具体是推导左子字符串重量范围(不是实际的桶索引)的方法,这样可以使该子字符串正好适合在radius内。我们将使用这个原语来推导任何数量子字符串的解决方案。
让目标父子字符串的重量为TW。
让目标左子字符串的重量为TL。
让目标右子字符串的重量为TR。
让搜索父子字符串的重量为SW。
设搜索左子串的权重为 SL。
设搜索右子串的权重为 SR。
TR = TW - TL
SR = SW - SL
设子串权重差的和为 SOD。
SOD = abs(TL - SL) + abs(TR - SR)
我们正在寻找满足 SOD <= 半径 的 TL。由于表达式中存在两个 abs,因此 SOD 有两个拐点。在这两个拐点之间,只有四种可能的组合
TL正向接近SL,而TR正向接近SR(斜率为-2)。TL首先达到其拐点,开始从SL和TR离开,而TR仍在向SR移动(斜率为0)。TR首先达到其拐点,开始从SR离开,而TL仍在向SL移动(斜率为0)。TL和TR都已达到它们的拐点,并且分别从SL和SR离开(斜率为2)。
正如我们所见,无论 TL 还是 TR 首先达到拐点,我们都可以保证在最终拐点之前斜率为 0。这是因为 TL 和 TR 是反向相关的。
我们必须首先计算第一个斜率会与半径相交的地方。我们假设 TL 低于或等于 SL,并且 TR 高于或等于 SR。根据这一点,我们知道当 (SL - TL) + (TR - SR) = 半径 时,我们进入搜索区域。由于 TR = TW - TL,我们可以将此重写为 (SL - TL) + (TW - TL - SR) = 半径。由于在此点 SR、SL 和 TW 都是已知的,我们可以解出 TL
TL = (-radius+ SL - SR + TW) / 2
让我们对相反的情况(斜率 2 达到 radius)做同样的事情
(TL - SL) + (SR - TR) =radius
(TL - SL) + (SR - TW + TL) =radius
TL = (radius+ SL - SR + TW) / 2
我们可以看到这两个方程有一个共同的截距,但我们不会直接提取截距,因为我们如果先除以 2 再相加就会失去一点精度。
令 C = SL - SR + TW。
我们必须在 (-半径 + C) / 2..=(半径 + C) / 2 的范围内进行搜索。然而,这假设存在任何匹配。半径可能低到没有匹配。在这种情况下,我们可以测试 0 斜率的情况。我们只需要测试 TL = (半径 + C) / 2 是否确实是一个匹配。为了测试这一点
abs((radius+C) / 2 - SL) + abs(TW - (radius+C) / 2 - SR) <=radius.
如果测试成功,那么我们可以安全地遍历范围。
让我们将这种推理应用到之前提到的树上。我们预计会得到范围 2..=3。
C= SL - SR + TW = 3 - 2 + 4 = 5
现在我们需要测试 abs((半径 + C) / 2 - SL) + abs(TW - (半径 + C) / 2 - SR) <= 半径。
abs((1 + 5) / 2 - 3) + abs(4 - (1 + 5) / 2 - 2) <= 1
abs(6 / 2 - 3) + abs(4 - 6 / 2 - 2) <= 1
abs(0) + abs(-1) <= 1
1 <= 1
测试通过。现在我们计算范围。
(-radius+C) / 2..=(radius+C) / 2
(-1 + 5) / 2..=(1 + 5) / 2
4 / 2..=6 / 2
2..=3
这是我们预期的范围。
我们可能还需要将范围裁剪到桶内,因为半径可能覆盖比范围更大的汉明距离集。
现在我们希望找到所有导致半径以下的子串组合。为此,我们需要知道在给定子串中搜索的每个索引处的 SOD。为了做到这一点,我们必须描述 TL 和 SOD 之间的关系。
TL 迭代模式中有三个阶段。第一个是当 半径 下降时,第二个是当它保持平坦时,第三个是当它上升时。最后部分的测试确保了底部在半径之上。我们需要计算斜率变为 0 的点,即拐点。幸运的是,这些很容易计算。它们是当 SOD 中的 abs 表达式的内部等于 0 时。
TL - SL = 0
TR - SR = 0
我们还知道 TR = TW - TL,因此我们可以用 TL 来重写这个表达式。
TW - TL - SR = 0
当我们到达拐点时,我们关注 TL。
TL = SL
TL = -SR + TW
我们不关心第一个到达的拐点是哪一个,我们只想知道它在哪。我们只需要取这两个表达式的 min 和 max,以得到曲线平直部分的起始和结束位置。
现在我们要解出 SOD。就像上次一样,我们以 TL 低于 SL 和 TR 高于 SR 开始。
(SL - TL) + (TW - TL - SR) = SOD
(TL - SL) + (SR - TW + TL) = SOD
我们可以简化这些,使其更清晰
C= SL - SR + TW
-2TL+C= SOD
2TL-C= SOD
它以 -2 的斜率开始下降,并以 2 的斜率上升,正如我们所预期的。
我们可以用这个表达式来计算每个迭代部分的 SOD。
现在迭代被分为三个部分
(-radius +C) / 2..SL(SOD = -2TL +C)SL..-SR + TW(SOD = -2SL +C)-SR +TW..=(radius +C) / 2(SOD = 2TL - C)
此时,我们可以计算所有输入索引的 SOD。现在我们遍历所有指定的输入索引,计算它们的 SOD,然后通过传递一个 new_radius 的 new_radius = radius - SOD 来搜索后续子字符串。这保证了该子字符串中的所有路径也不会超过该级别的所有子字符串的总 SOD。
最近邻
当我们使用上述半径搜索算法时,我们搜索每个可能位于特定半径或更低的特征。不幸的是,当我们在一个汉明权重树中寻找最近邻时,我们必须从半径 0 开始搜索,然后是半径 1,以此类推。如果我们使用上述算法,由于汉明空间有极其厚的边界(见论文《二进制空间中的厚边界及其对最近邻搜索的影响》),可能有一个很大的比例的整个汉明空间与最近邻等距。这意味着我们的搜索算法将使我们在空间中测试所有这些地方,如果它们在树中有表的话。
依赖关系
~3.5MB
~60K SLoC