5个版本 (3个破坏性更新)
| 0.4.0 | 2020年9月12日 |
|---|---|
| 0.3.0 | 2020年9月11日 |
| 0.2.0 | 2020年9月11日 |
| 0.1.1 | 2020年9月11日 |
| 0.1.0 | 2020年9月11日 |
#2168 在 算法
27KB
429 行
Graph Solver
无向图节点和边颜色约束求解器。
由AdvancedResearch社区提供!
- 如果您正在寻找一个不删除事实的通用求解器,请参阅monotonic_solver
- 如果您正在寻找一个可以删除事实的通用求解器,请参阅linear_solver
- 如果您正在寻找经典和路径语义逻辑的暴力自动定理证明器,请参阅pocket_prover
动机
图求解用于找到各种代数的视觉表示,如Adinkra图表,但生成图的高效规则是未知的。
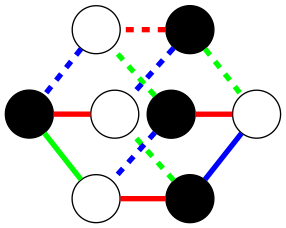
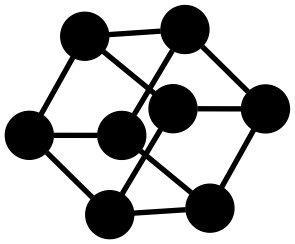
示例:立方体
使用图求解器构建立方体需要指定节点如何连接到其他节点。您提供给求解器的信息是这些连接的颜色,但没有告诉图中哪些节点应该连接。
/*
=== CUBE EXAMPLE ===
Run with GraphViz (https://graphviz.cn/):
cargo run --example cube | dot -Tpng > test.png
*/
use graph_solver::*;
// Notice that edges starts with `2`.
// This is because `0` is empty and `1` is no-edge.
const EDGE: Color = 2;
fn main() {
let mut g = Graph::new();
// Create a node pattern with 3 edges.
let a = Node {
color: 0,
self_connected: false,
edges: vec![Constraint {edge: EDGE, node: 0}; 3]
};
// Add 8 vertices.
for _ in 0..8 {g.push(a.clone())}
g.no_triangles = true;
let solve_settings = SolveSettings::new();
if let Some(solution) = g.solve(solve_settings) {
println!("{}", solution.puzzle.graphviz(
"sfdp",
&["black"],
&["black"]
));
} else {
eprintln!("<no solution>");
}
}
图约束求解简介
每个节点都有一个颜色和一条边约束列表。边约束存储一个边颜色和相邻节点的目标颜色。
这种技术创建了一种强大的语言来紧凑地描述图。例如,所有局部相似的节点可以使用相同的描述。
任何图都可以使用关于节点和边的足够局部信息来确定。为此,可以给每个节点和边分配一个唯一的数字。
因此,为了更详细地描述图,可以简单地添加更多颜色!
设计
使用quickbacktrack库进行约束求解。
这允许从部分解决的图开始,覆盖求解策略,调试或比较解决方案与原始内容。
- 节点和边颜色表示为
u64 - 节点颜色可以是任何值
- 边颜色通常从
2开始 - 边颜色
0表示无选择(既不是空的也不是彩色的)。 - 边颜色
1表示空
依赖项
~54KB