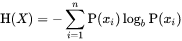entropy

entropy 是一个用于计算给定文件香农熵的小型实用程序。

tuxⒶlattice:[~] => ./entropy --help
entropy 1.0.0
tux <me@johnpacific.com>
A utility to calculate Shannon entropy of a given file

USAGE:
    entropy [FLAGS] <filepath>

ARGS:
    <filepath>    The target file to measure

FLAGS:
    -h, --help              Prints help information
    -m, --metric-entropy    Returns metric entropy instead of Shannon entropy
    -V, --version           Prints version information

用法

要计算给定文件的香农熵，只需

tuxⒶlattice:[~] => ./entropy path/to/file.bin
4.142214

要计算给定文件的度量熵，请添加 --metric-entropy 标志

tuxⒶlattice:[~] => ./entropy path/to/file.bin --metric-entropy
0.5177767

什么是香农熵？

香农熵可以描述为字符串中的“信息量”。它可以从以下方程式中计算出来：

此方程的输出（在 log_2 中执行时）可以告诉您编码“信息”或“符号”所需的最低位数。

度量熵是通过将香农熵除以符号的长度来计算的。由于我们通过 log_2 计算香农熵（以位为单位）并按字节计数，因此我们将香农熵除以八（字节的位数）。

度量熵的输出是介于 0 和 1 之间的数字，其中 1 表示信息（或符号）在字符串中均匀分布。这可以用来评估特定字符串的“随机性”或“不确定性”。它还可以作为指标，表明当度量熵接近 0 时，数据可能被有效地压缩。

演示

让我们计算来自 /dev/urandom 的一个 真正 随机文件的香农熵和度量熵

tuxⒶlattice:[~] => cat /dev/urandom | head -c 1000000 > random.bin

因此，我们使用 /dev/urandom 填充了一个 1MB 的随机数据文件。内部数据应该是均匀分布的，但我们来验证这一点

tuxⒶlattice:[~] => ./entropy random.bin
7.9998097
tuxⒶlattice:[~] => ./entropy random.bin --metric-entropy
0.9999762

如上图所示，香农熵表明我们需要用八个位来编码文件中的每个符号。度量熵表明 random.bin 文件中的信息是均匀分布的；它充满了信息！

那么，如果我们从全部为零的文件中做同样的事情会发生什么？让我们来看看

tuxⒶlattice:[~] => cat /dev/zero | head -c 1000000 > zero.bin
tuxⒶlattice:[~] => ./entropy zero.bin
0
tuxⒶlattice:[~] => ./entropy zero.bin --metric-entropy
0

香农熵和度量熵为零！为什么？因为文件中没有唯一的符号。在这个文件中找到零的概率正好是1；不可能在文件中找到非零符号。因此，我们不需要任何额外信息来将其编码为二进制序列。

有关更多信息，请参阅关于此主题的优秀维基百科条目.

如果这个仓库对您有所帮助，请与我联系并告诉我！我很乐意听听您的意见！