3 个版本
| 0.1.2 | 2022 年 2 月 23 日 |
|---|---|
| 0.1.1 | 2021 年 11 月 24 日 |
| 0.1.0 | 2021 年 11 月 23 日 |
#4 in #cess
在 2 crates 中使用
690KB
15K SLoC
CESS 存储证明 PoRep
cess-sp-porep 是 复制证明 (PoRep) 的参考实现，并为 cess-proofs 执行所有繁重的工作。
复制证明 证明存储矿工为每个扇区分配了唯一的存储空间。矿工在扇区中收集新客户端的数据，运行慢速编码过程（称为 Seal）并生成证明（SealProof），证明编码是正确生成的。
PoRep 提供两项保证
- 空间复杂度：存储矿工无法就其分配给 CESS 网络的存储空间量说谎，以获取更多权力。
- 复制：存储矿工为客户端数据的每个副本分配了唯一的存储空间。
复制证明 使用由 Ben Fisch 在 EUROCRYPT19 设计的堆叠 DRG（SDR）。SDR 使用深度鲁棒图来确保扇区已使用慢速且不可并行的顺序过程进行编码。
在 SDR 中的证明大小太大，无法存储在区块链中，这主要是因为需要大量的梅克尔树证明来实现安全性。SDR 验证算法是使用算术电路构建的，并使用 SNARKs 来证明 SDR 证明已被正确评估。
PoRep 电路
PoRep 电路概述
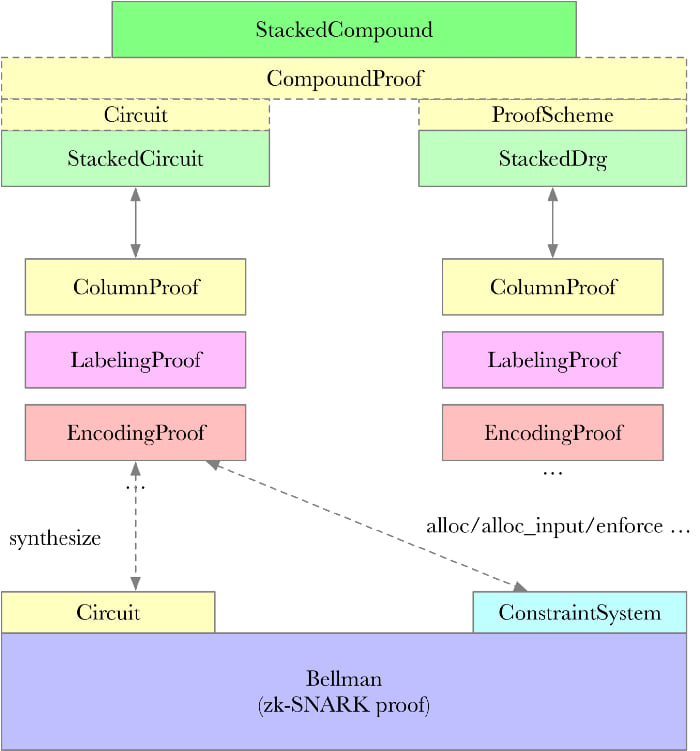图片来源：Star LI
StackedCircuit
StackedCircuit 是 PoRep 的整体电路，定义在 proof.rs
pub struct StackedCircuit<'a, Tree: 'static + MerkleTreeTrait, G: 'static + Hasher> {
public_params: <StackedDrg<'a, Tree, G> as ProofScheme<'a>>::PublicParams,
replica_id: Option<<Tree::Hasher as Hasher>::Domain>,
comm_d: Option<G::Domain>,
comm_r: Option<<Tree::Hasher as Hasher>::Domain>,
comm_r_last: Option<<Tree::Hasher as Hasher>::Domain>,
comm_c: Option<<Tree::Hasher as Hasher>::Domain>,
// one proof per challenge
proofs: Vec<Proof<Tree, G>>,
}
这包括
- public_params：堆叠 DRG（深度鲁棒图）相关参数，包括图本身的参数和挑战次数。
- replica_id：扇区副本 ID
- comm_d：原始数据二叉树根
- comm_r：comm_r_last 和 comm_c 的哈希结果
- comm_r_last：编码后数据的八叉树的根
- comm_c：列哈希结果的八叉树根
- proofs：挑战相应的证明电路
整个电路的构建从synthesize接口函数的StackedCircuit开始。
impl<'a, Tree: MerkleTreeTrait, G: Hasher> Circuit<Fr> for StackedCircuit<'a, Tree, G> {
fn synthesize<CS: ConstraintSystem<Fr>>(self, cs: &mut CS) -> Result<(), SynthesisError> {
let StackedCircuit {
public_params,
proofs,
replica_id,
comm_r,
comm_d,
comm_r_last,
comm_c,
..
} = self;
//... // function body.
Ok(())
}
}
此函数将电路分为两部分
- 树根检查电路
- 挑战节点信息证明电路
Tree root check circuit相当简单，用于验证comm_r是否正确地使用comm_c和comm_r_last计算。另一方面，Challenge node proof circuit根据扇区的大小生成挑战节点证明电路。对于32GiB扇区，生成176个挑战。也称为176个小电路。
for (i, proof) in proofs.into_iter().enumerate() {
proof.synthesize(
&mut cs.namespace(|| format!("challenge_{}", i)),
public_params.layer_challenges.layers(),
&comm_d_num,
&comm_c_num,
&comm_r_last_num,
&replica_id_bits,
)?;
}
每个挑战节点的这些小电路由在params.rs中定义的Proof结构表示。
标记
标记节点 Stacked-DRG中每个节点的标记函数为Sha254，生成一个254位的域元素。每个节点层元组在副本的Stacked-DRG中都有一个唯一的预像。
标记计算的证明电路是为了证明某个节点是根据SDR算法正确计算的。
generate_labels函数描述了如何为副本标记每个Stacked-DRG节点。第一层的节点仅使用DRG父节点的标记进行标记，后续每一层的节点都使用其DRG和expander父节点的标记进行标记。每一层的第一个节点不使用父节点进行标记。
可以通过调用以下函数创建LabelingProof对象
impl<H: Hasher> LabelingProof<H> {
pub fn new(layer_index: u32, node: u64, parents: Vec<H::Domain>) -> Self {
LabelingProof {
node,
layer_index,
parents,
_h: PhantomData,
}
}
...
}
create_label函数计算replica_id、layer_index和连接到缓冲区的node id以及父节点的哈希值的sha256。
以下代码用于验证之前步骤生成的所有标签。此函数仅通过比较labeling_proof与label_node来检查质量。
/// Verify all labels.
fn verify_labels(
&self,
replica_id: &<Tree::Hasher as Hasher>::Domain,
layer_challenges: &LayerChallenges,
) -> bool {
// Verify Labels Layer 1..layers
...
}
编码
编码是将扇区转换为编码副本的过程。编码函数是节点-wise素域加法，其中"节点-wise"表示扇区的每个不同部分都是离散编码的。属于扇区的每个不同部分都被解释为一个域元素，并通过将其密钥添加到切片中编码到副本。
使用从R的ReplicaId派生的编码密钥（K）使用encode函数将扇区（D）编码到副本（R）。
pub fn encode<T: Domain>(key: T, value: T) -> T {
let mut result: Fr = value.into();
let key: Fr = key.into();
result += key;
result.into()
}
复制
复制是一个将扇区D唯一编码到副本R的过程。复制包括Stacked-DRG标记、将D编码到R以及生成TreeC（在Labels上）和TreeR（在R上）的树。
矿工使用对副本扇区的承诺CommD = TreeD.root（其中TreeD是在与R相关的编码扇区D的节点上构建的）为每个R推导出一个唯一的ReplicaID。
给定一个扇区D及其承诺CommD，复制过程如下
生成R的唯一ReplicaID。从ReplicaID生成Labels，从而推导出关键的K，该K将D编码到R中。通过列承诺过程在Labels的列上生成TreeC。使用编码密钥K将D编码到R中。在副本R上生成一个TreeR: OctTree。通过承诺CommCR对R及其相关的标签Labels进行承诺。
函数replicate运行一个扇区D的整个复制过程。
副本ID生成
函数generate_replica_id描述了一个拥有ProverID的矿工如何为扇区D的副本R生成一个ReplicaID，其中D具有唯一的sectorID和承诺CommD。证明者对每个生成的ReplicaID使用一个唯一的随机值R。
扇区构建
扇区D由CESS客户端数据构建而成，客户端数据已预先处理/填充，使得两个零位位于每个不同的254位客户端数据切片之间。此填充过程产生的扇区D使得每个256位切片代表一个有效的254位字段元素。
为扇区D构建一个Merkle树TreeD: BinTree，其叶子是256位切片Di。每个TreeD都是基于预先处理过的扇区数据D构建的。
PoRep挑战
函数derive_internal为副本R的分区-k PoRep分区证明创建PoRep挑战集。
Bellman
“zk-SNARKs是一种密码学技术，允许证明者有效地说服验证者他知道某些信息——但又不泄露信息本身。zk-SNARKs由于其（知识）正确性属性：即使它们保持私密，也不能在没有正确陈述的知识的情况下创建有效证明，因此在区块链设置中允许与未知和不信任的各方进行安全、私密的交互。” ——来自Filecoin。
cess-proving-system使用"Bellman's zk-SNARs"实现，主要基于BLS12-381椭圆曲线，并实现了Groth16的零知识证明系统。这个库用于验证零知识证明是否正确，验证过程大约需要几毫秒，使其相对较快。
许可证
MIT或Apache 2.0
依赖关系
~23–34MB
~524K SLoC