3 个稳定版本
| 1.0.2 | 2024年5月21日 |
|---|---|
| 1.0.1 | 2024年5月3日 |
#261 在 算法 中
每月305 次下载
440KB
982 行
cardinality-estimator
cardinality-estimator 是一个Rust crate,旨在以高效的方式估计流或数据集中不同元素的数量。该库使用HyperLogLog++,具有优化的低内存占用和高度精确的方法,适用于大规模数据分析任务。我们在大规模机器学习中使用 cardinality-estimator,在请求的多个维度上计算基数特征。
概述
我们的 cardinality-estimator 在内存使用、延迟和精度方面都非常高效。这是通过利用独特的数据结构设计、高效算法以及HyperLogLog++对高基数范围的优化来实现的。
入门指南
要使用 cardinality-estimator,请将其添加到您的 Cargo.toml 中的 [dependencies]
[dependencies]
cardinality-estimator = "1.0.0"
然后,在您的Rust程序中导入 cardinality-estimator
use cardinality_estimator::CardinalityEstimator;
let mut estimator = CardinalityEstimator::<12, 6>::new();
estimator.insert("test");
let estimate = estimator.estimate();
println!("estimate = {}", estimate);
低内存占用
cardinality-estimator 通过利用高效的数据存储格式实现低内存占用。数据以三种不同的表示形式存储 - Small、Array 和 HyperLogLog,具体取决于基数范围。例如,对于基数为0到2的情况,只使用 8字节 的堆栈内存和0字节的堆内存。
低延迟
该crate通过使用编译器提示进行自动向量化切片操作,实现低延迟。随着更多数据的插入,动态存储和更新零寄存器和寄存器谐波和,从而实现快速的估计操作。
高精度
通过为小基数范围使用精确计数以及为较大范围使用带有LogLog-Beta偏差校正的HyperLogLog++,基数估计器实现了高精度。这为大型基数提供了低至0.02%的预期误差率。
基准测试
要运行基准测试,您首先需要安装 cargo-criterion 二进制文件
cargo install cargo-criterion
然后以 JSON 格式输出基准测试结果以供进一步分析
make bench
我们已经将基数估计器与其他几个生态系统中的 crate 进行了基准测试
请注意,hyperloglog 和 probabilistic-collections crate 中存在基于提供的 probability 计算精度 p 的错误
- 错误的公式:
p = (1.04 / error_probability).powi(2).ln().ceil() as usize; - 正确的公式:
p = (1.04 / error_probability).powi(2).log2().ceil() as usize;
我们正在努力使 cardinality-estimator 成为 Rust 中最快的、最轻量级的和最精确的基数估计工具。
以下基准测试是在 Linux 笔记本电脑上执行的,使用 13th Gen Intel(R) Core(TM) i7-13800H 处理器,并将编译器标志设置为 RUSTFLAGS=-C target-cpu=native。
内存使用情况
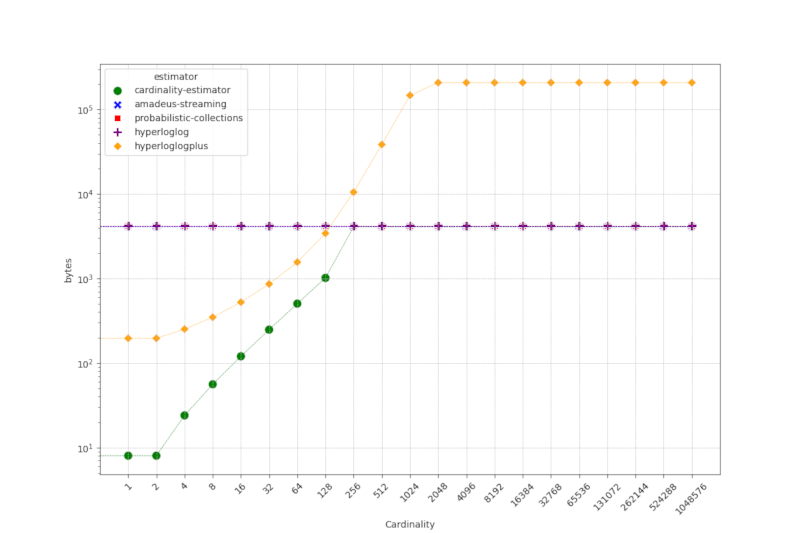
下表比较了不同基数估计器的内存使用情况。每个单元格中的数字表示在每次测量的基数下 栈内存字节 / 堆内存字节 / 堆内存块。
我们的 cardinality-estimator 在所有不同的基数下都实现了最低的栈和堆内存分配。
请注意,hyperloglogplus 实现的内存使用量尤其高,特别是对于基数大于 256 的情况。
| 基数 | cardinality_estimator | amadeus_streaming | probabilistic_collections | hyperloglog | hyperloglogplus |
|---|---|---|---|---|---|
| 0 | 8 / 0 / 0 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4464 / 2 | 160 / 0 / 0 |
| 1 | 8 / 0 / 0 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 36 / 1 |
| 2 | 8 / 0 / 0 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 36 / 1 |
| 4 | 8 / 16 / 1 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 92 / 2 |
| 8 | 8 / 48 / 2 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 188 / 3 |
| 16 | 8 / 112 / 3 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 364 / 4 |
| 32 | 8 / 240 / 4 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 700 / 5 |
| 64 | 8 / 496 / 5 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 1400 / 13 |
| 128 | 8 / 1008 / 6 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 3261 / 23 |
| 256 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 10361 / 43 |
| 512 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 38295 / 83 |
| 1024 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 146816 / 163 |
| 2048 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 207711 / 194 |
| 4096 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 207711 / 194 |
| 8192 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 207711 / 194 |
| 16384 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 207711 / 194 |
| 32768 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 207711 / 194 |
| 65536 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 207711 / 194 |
| 131072 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 207711 / 194 |
| 262144 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 207711 / 194 |
| 524288 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 207711 / 194 |
| 1048576 | 8 / 4092 / 7 | 48 / 4096 / 1 | 128 / 4096 / 1 | 120 / 4096 / 1 | 160 / 207711 / 194 |
插入性能
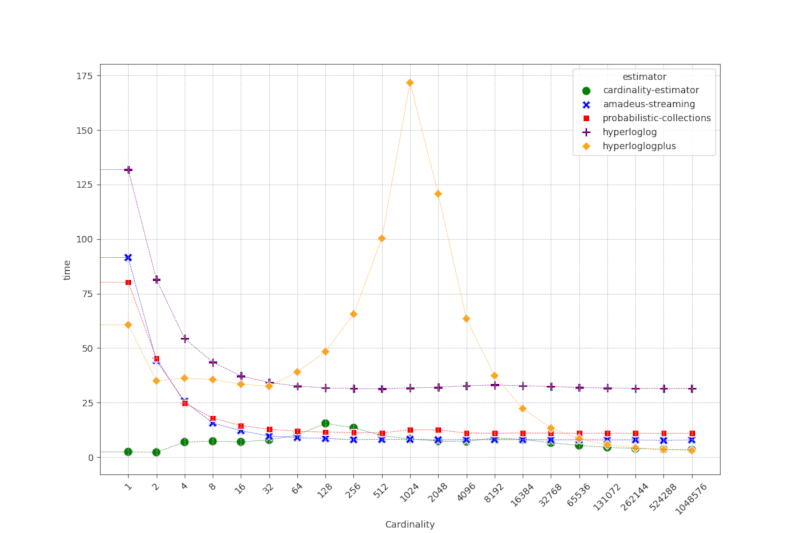
下表表示每个元素的插入时间(纳秒)。
我们的 cardinality-estimator 在大多数基数下都表现出最低的插入时间。
| 基数 | cardinality-estimator | amadeus-streaming | probabilistic-collections | hyperloglog | hyperloglogplus |
|---|---|---|---|---|---|
| 0 | 0.64 | 88.12 | 70.19 | 82.69 | 17.45 |
| 1 | 2.42 | 91.5 | 80.2 | 131.86 | 60.65 |
| 2 | 2.21 | 44.3 | 45.34 | 81.48 | 34.96 |
| 4 | 6.9 | 25.59 | 24.85 | 54.38 | 36.22 |
| 8 | 7.27 | 15.62 | 17.92 | 43.54 | 35.55 |
| 16 | 6.99 | 12.15 | 14.44 | 37.24 | 33.4 |
| 32 | 7.9 | 9.6 | 12.78 | 34.23 | 32.49 |
| 64 | 10.14 | 8.97 | 11.86 | 32.55 | 39.04 |
| 128 | 15.47 | 8.52 | 11.49 | 31.76 | 48.37 |
| 256 | 13.42 | 8.01 | 11.24 | 31.44 | 65.58 |
| 512 | 9.92 | 8.1 | 11.11 | 31.34 | 100.25 |
| 1024 | 8.32 | 8.14 | 12.52 | 31.73 | 171.71 |
| 2048 | 7.31 | 7.92 | 12.52 | 32.03 | 120.71 |
| 4096 | 7.11 | 8.01 | 11.04 | 32.73 | 63.5 |
| 8192 | 8.81 | 8.02 | 10.97 | 33.08 | 37.36 |
| 16384 | 8.08 | 8.01 | 11.03 | 32.75 | 22.24 |
| 32768 | 6.55 | 7.96 | 11.01 | 32.37 | 13.3 |
| 65536 | 5.35 | 7.96 | 10.96 | 31.95 | 8.41 |
| 131072 | 4.48 | 7.9 | 10.97 | 31.71 | 5.71 |
| 262144 | 3.91 | 7.95 | 10.95 | 31.52 | 4.26 |
| 524288 | 3.58 | 7.64 | 10.95 | 31.47 | 3.47 |
| 1048576 | 3.35 | 7.95 | 10.95 | 31.47 | 3.04 |
估计性能
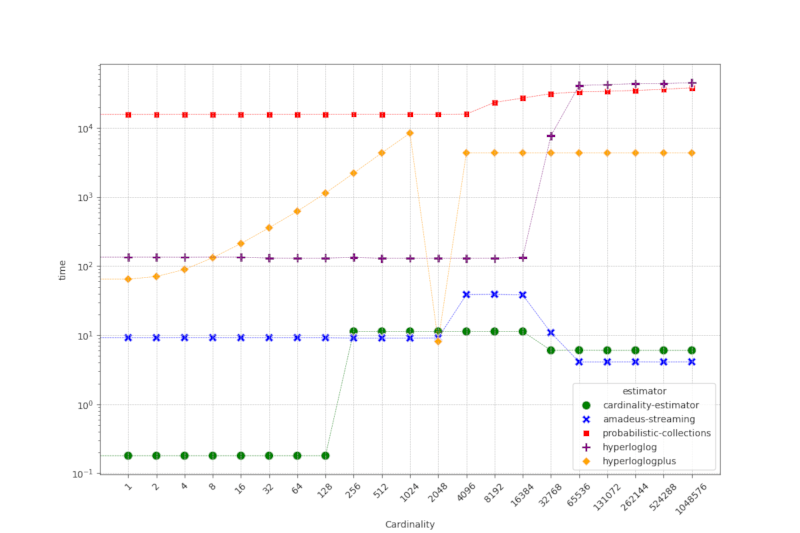
下表表示每次调用的估计时间(纳秒)。
我们的 cardinality-estimator 在大多数基数下,特别是 128 以下的较小基数中,都显示了最低的估计时间。
请注意,amadeus-streaming 的实现对于估计操作也非常有效,然而,如上表所示,它的内存使用量更高。实现 probabilistic-collections、hyperloglogplus 和 hyperloglogplus 的估计时间要高得多,尤其是在高基数情况下。
| 基数 | cardinality-estimator | amadeus-streaming | probabilistic-collections | hyperloglog | hyperloglogplus |
|---|---|---|---|---|---|
| 0 | 0.18 | 7.9 | 15576.4 | 125.03 | 24.89 |
| 1 | 0.18 | 9.19 | 15619.8 | 134.3 | 64.62 |
| 2 | 0.18 | 9.18 | 15615.5 | 134.4 | 70.51 |
| 4 | 0.18 | 9.2 | 15642.7 | 134.01 | 89.16 |
| 8 | 0.18 | 9.19 | 15611.1 | 134.41 | 132.0 |
| 16 | 0.18 | 9.19 | 15621.6 | 134.39 | 211.4 |
| 32 | 0.18 | 9.19 | 15637.1 | 130.58 | 357.55 |
| 64 | 0.18 | 9.19 | 15626 | 130.26 | 619.95 |
| 128 | 0.18 | 9.18 | 15640.8 | 130.33 | 1134.12 |
| 256 | 11.31 | 9.09 | 15668 | 133.5 | 2205.7 |
| 512 | 11.3 | 9.09 | 15652 | 129.58 | 4334.05 |
| 1024 | 11.31 | 9.09 | 15687.1 | 129.79 | 8392.59 |
| 2048 | 11.28 | 9.11 | 15680.4 | 129.8 | 8.08 |
| 4096 | 11.29 | 38.63 | 15803.4 | 129.49 | 4342.07 |
| 8192 | 11.28 | 38.98 | 23285 | 129.51 | 4345.7 |
| 16384 | 11.29 | 38.17 | 26950.7 | 132.96 | 4341.9 |
| 32768 | 6.02 | 10.86 | 31168 | 7674.3 | 4334.98 |
| 65536 | 6.05 | 4.1 | 33123.8 | 40986.4 | 4327.48 |
| 131072 | 6.02 | 4.1 | 33772.4 | 42113.7 | 4327.29 |
| 262144 | 6.02 | 4.11 | 34711.7 | 43587 | 4329.63 |
| 524288 | 6.02 | 4.1 | 36091.2 | 43582.8 | 4327.8 |
| 1048576 | 6.02 | 4.11 | 37877.1 | 45055.3 | 4327.37 |
错误率
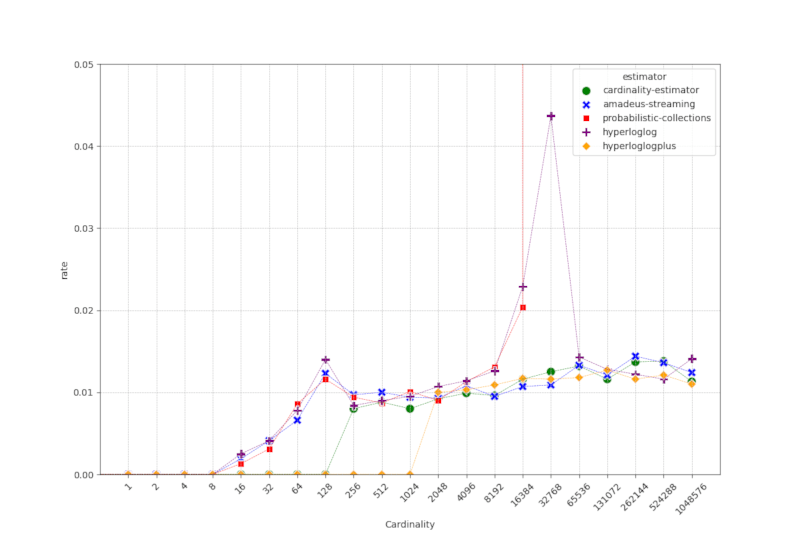
下表展示了在给定基数下,估计器在随机元素上运行100次后的平均绝对相对误差。
我们的 cardinality-estimator 在性能上与 amadeus-streaming 和 hyperloglog 估计器相当,但在基数高达128时,具有特别小的低错误率。
请注意,probabilistic-collections 实现在基数 >=32768 时的估计操作中似乎存在错误。
| 基数 | cardinality_estimator | amadeus_streaming | probabilistic_collections | hyperloglog | hyperloglogplus |
|---|---|---|---|---|---|
| 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 4 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 8 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 16 | 0.0000 | 0.0019 | 0.0013 | 0.0025 | 0.0000 |
| 32 | 0.0000 | 0.0041 | 0.0031 | 0.0041 | 0.0000 |
| 64 | 0.0000 | 0.0066 | 0.0086 | 0.0078 | 0.0000 |
| 128 | 0.0000 | 0.0123 | 0.0116 | 0.0140 | 0.0000 |
| 256 | 0.0080 | 0.0097 | 0.0094 | 0.0084 | 0.0000 |
| 512 | 0.0088 | 0.0100 | 0.0087 | 0.0090 | 0.0000 |
| 1024 | 0.0080 | 0.0094 | 0.0101 | 0.0095 | 0.0000 |
| 2048 | 0.0092 | 0.0093 | 0.0090 | 0.0107 | 0.0100 |
| 4096 | 0.0099 | 0.0108 | 0.0113 | 0.0114 | 0.0103 |
| 8192 | 0.0096 | 0.0095 | 0.0131 | 0.0126 | 0.0109 |
| 16384 | 0.0116 | 0.0107 | 0.0204 | 0.0229 | 0.0117 |
| 32768 | 0.0125 | 0.0109 | 1.46e14 | 0.0437 | 0.0116 |
| 65536 | 0.0132 | 0.0133 | 2.81e14 | 0.0143 | 0.0118 |
| 131072 | 0.0116 | 0.0121 | 1.41e14 | 0.0128 | 0.0127 |
| 262144 | 0.0137 | 0.0144 | 7.04e13 | 0.0122 | 0.0116 |
| 524288 | 0.0138 | 0.0136 | 3.52e13 | 0.0116 | 0.0121 |
| 1048576 | 0.0113 | 0.0124 | 1.76e13 | 0.0141 | 0.0110 |
| 平均 | 0.0064 | 0.0078 | 3.14e13 | 0.0101 | 0.0052 |