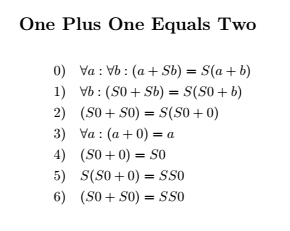8个版本 (3个稳定版)
| 1.0.2 | 2022年11月18日 |
|---|---|
| 1.0.1 | 2021年4月15日 |
| 0.4.1 | 2021年4月4日 |
| 0.4.0 | 2021年3月30日 |
| 0.1.1 | 2021年3月25日 |
在数学类别中排名788
每月下载量36次
205KB
1.5K SLoC
tnt
实现了Hofstader的《哥德尔、艾舍尔、巴赫:集异璧之大成》一书中“打字机数论”。该crate允许使用命题逻辑创建数论简单证明。它不是一个证明辅助工具,不能创建给定公式的证明或反证,而是通过Deduction结构在运行时强制执行推理规则,以防止创建无效的证明。某些无意义的构造也在编译时被捕获。
有关说明的简要解释可在入门指南中找到。
一旦创建Deduction,就可以以各种方式输出。
考虑以下证明1 + 1 = 2的简短证明。
use tnt::types::{Term, Variable, Number};
use tnt::deduction::Deduction;
use tnt::axioms::PEANO;
let a = &Variable::new("a");
let b = &Variable::new("b");
let zero = &Number::zero();
let one = &Number::one();
let mut d = Deduction::new("One Plus One Equals Two", PEANO.clone());
d.add_axiom(&PEANO[2])?; // Aa:Ab:(a+Sb)=S(a+b)
d.specification(0, a, one)?;
d.specification(1, b, zero)?;
d.add_axiom(&PEANO[1])?;
d.specification(3, a, one)?;
d.successor(4)?;
d.transitivity(2, 5)?;
使用 .pretty_print()
0) Aa:Ab:(a+Sb)=S(a+b)
1) Ab:(S0+Sb)=S(S0+b)
2) (S0+S0)=S(S0+0)
3) Aa:(a+0)=a
4) (S0+0)=S0
5) S(S0+0)=SS0
6) (S0+S0)=SS0
使用 .latex("addition") 我们得到以下内容的文件 addition.tex
\documentclass[fleqn,11pt]{article}
\usepackage{amsmath}
\allowdisplaybreaks
\begin{document}
\section*{One Plus One Equals Two}
\begin{flalign*}
&\hspace{0em}0)\hspace{1em}\forall a:\forall b:(a+Sb)=S(a+b)\\
&\hspace{0em}1)\hspace{1em}\forall b:(S0+Sb)=S(S0+b)\\
&\hspace{0em}2)\hspace{1em}(S0+S0)=S(S0+0)\\
&\hspace{0em}3)\hspace{1em}\forall a:(a+0)=a\\
&\hspace{0em}4)\hspace{1em}(S0+0)=S0\\
&\hspace{0em}5)\hspace{1em}S(S0+0)=SS0\\
&\hspace{0em}6)\hspace{1em}(S0+S0)=SS0\\
\end{flalign*}
渲染结果如下
Deduction还可以通过使用 .english() 方法进行粗略的英文翻译,并自动添加注释。
0) for all a and b, (a + (b + 1)) = ((a + b) + 1) [axiom]
1) for all b, (1 + (b + 1)) = ((1 + b) + 1) [specification of a to S0 in theorem 0]
2) (1 + 1) = ((1 + 0) + 1) [specification of b to 0 in theorem 1]
3) for all a, (a + 0) = a [axiom]
4) (1 + 0) = 1 [specification of a to S0 in theorem 3]
5) ((1 + 0) + 1) = 2 [successor of theorem 4]
6) (1 + 1) = 2 [transitivity of theorem 2 and theorem 5]
最后,通过使用 .arithmetize() 方法,Deduction可以表示为一个(非常大的)整数,该整数将每个定理作为字节(由空格分隔)读入BigUint。作者知道这没有任何实际用途,但对于生产哥德尔语句是相关的。
前面的定理对应于以下数字:1050341303275422378657768361784977847949672579265786753539438511912991722480303393035798790127074435266152493569318923916943104808524883160525578709392832871799037992734723295688338121067685795026664762465244602602804284806503763532291647776
未来目标
目前 .english() 方法依赖于手动解析器。这应该改为像pest或nom这样的crate,以避免错误。
为Deduction提供更好的文档。
依赖项
~5.5–7.5MB
~137K SLoC