SOCAREL

Rust crate，用于生成、操作和遍历树。

它提供了8种不同遍历算法的迭代器。
以O(1)的复杂度添加和删除节点。以O(p)的复杂度在路径中查找节点（其中p是路径长度）。
支持自定义节点模型以创建复杂的树格式。

用法 & 文档

与任何crate一样，使用cargo生成文档

cargo doc --open

crate

在 crates.io 下载crate

示例

查看文件 src/main.rs 和 src/tests.rs 了解用法示例。

名称

Socarel 是一个加泰罗尼亚语单词，由 soca（树干）和 rel（根）组成。意思是完全的，全部的，根据上下文可以理解为纯粹的，真正的。

lib.rs:

SOCAREL

Socarel 是一个用于生成、操作和遍历树的库。

它提供了8种不同遍历算法的迭代器。
以O(1)的复杂度添加和删除节点。以O(p)的复杂度在路径中查找节点（其中p是路径长度）。
支持自定义节点模型以创建复杂的树格式。

示例

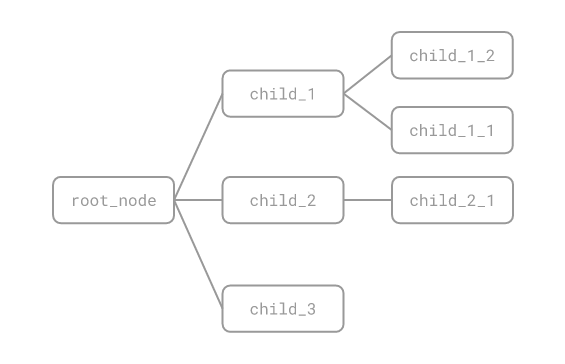
要生成如下所示的树

我们会这样做

use socarel::*;

let mut tree = <Tree>::new();
let _root_node = tree.set_root("root_node").unwrap();
let _child_1 = tree.link_node("child_1", _root_node).unwrap();
let _child_2 = tree.link_node("child_2", _root_node).unwrap();
let _child_3 = tree.link_node("child_3", _root_node).unwrap();
let _child_1_1 = tree.link_node("child_1_1", _child_1).unwrap();
let _child_1_2 = tree.link_node("child_1_2", _child_1).unwrap();
let _child_2_1 = tree.link_node("child_2_1", _child_2).unwrap();

然后你可以将你的树存储在森林中

let mut forest = <Forest>::new();
forest.add_tree("my_tree", tree);

稍后可以检索它

let tree = forest.get_tree("my_tree").unwrap();

或迭代森林以获取所有树

for (tree_id, tree) in forest.iter() {
    // ...
}

编辑树

当然，在创建后也可以修改树，当然是通过链接更多节点，就像我们之前看到的那样，但也可以取消链接它们

let tree = forest.get_mut_tree("my_tree").unwrap();
tree.unlink_node(_child_1);
tree.unlink_node(_child_2);

取消链接后，节点仍然在存储在 Tree 内的节点数组中，但无法访问，因为它与树的其他部分断开连接。并且任何取消链接节点的子节点也无法访问。因此，在两次取消链接操作之后，树将只剩下两个节点：root_node 和 child_3。

但我们为什么还留下这些节点呢？我们在浪费内存！是的，但替代方案是递归删除所有节点，这可能是昂贵的，实际上也是不可预测的，因为我们不知道有多少子节点。为了保持取消链接操作快速 / O(1)，我们需要这样做。

我们还可以在不修改链接属性的情况下更改节点的内容

tree.update_node("new_root_node", _root_node);

迭代器

遍历树有很多方法，这就是为什么 Socarel 提供了多个迭代器，每个迭代器实现一种遍历算法。让我们看看最广泛使用的一种，BFS

for (node, node_index) in tree.iterators().bfs() {
    // ...
}

查看IterInterface以获取迭代器的完整列表。

查找节点

有时为了找到节点，我们不需要迭代器，因为我们知道它在树结构中的位置

let _node = tree.find_node(&["root_node", "child_1", "child_1_1"]).unwrap();

当可能时，使用[Tree::find_node()]始终是更好的选择，因为其复杂度为O(p)（p = 路径长度），而大多数遍历算法的复杂度为O(n)（n = 树中的节点数量）。

自定义节点

Tree包含一个Node数组，但当前的节点结构只提供了关于其在树中位置的信息，不提供存储内容的方式。内容存储在另一个实现NodeContent trait 的结构体中。

Socarel提供了一个默认实现RawNode，在未提供其他类型时使用。这就是我们之前创建树和森林实例的原因

let tree = <Tree>::new();

以及为什么它无法编译的原因

let tree = Tree::new();

因为Tree被定义为一个实现了NodeContent的泛型，它有一个默认类型RawNode。因此，我们也可以创建这样的树

let tree = Tree::<RawNode>::new();

但我们可以实现自己的节点内容来模拟我们想要的任何东西。想象一下，我们想要一个具有节点连接权重的树。我们可以定义类似的东西

struct WeightNode {
    content: String,
    weight: u32
}

impl WeightNode {
    fn get_weight(&self) -> u32 {
        self.weight
    }
}

impl NodeContent for WeightNode {
    // We parse the node content and return None if not a valid format
    fn new(content: &str) -> Option<Self> {
        let vec: Vec<&str> = content.split(':').collect();
        if vec.len() == 2 {
            match vec[0].trim().parse() {
                Ok(num) => Some(Self {
                    content: String::from(vec[1]),
                    weight: num
                }),
                Err(_) => None
            }
        }
        else {
            None
        }
    }

    fn get_val(&self) -> &str {
        &self.content
    }

    fn gen_content(&self) -> String {
        format!("{}:{}", self.weight, self.content)
    }
}

现在我们可以在树中使用我们全新的节点内容

let mut tree = Tree::<WeightNode>::new();
let _root = tree.set_root("0:my root node").unwrap();
let _node_1 = tree.link_node("10:my node 1", _root).unwrap();
let _node_1_1 = tree.link_node("100:child of my node 1", _node_1).unwrap();
for (node, _) in tree.iterators().bfs() {
    let cref = node.get_content_ref();
    println!("Node content = `{}` weight = {}", cref.get_val(), cref.get_weight());
}