C++、Rust和Python中的恒定Q滑动DFT

根据[1]实现正向和逆向恒定Q滑动DFT (QDFT)，具有以下特性

• 任意八度分辨率（默认为四分之一音
• 内置可参数化余弦家族窗口（默认为汉宁窗口）
• C++中可自定义时间和频率域数据类型
• 一次性处理单个或多个样本
• 可选的分析延迟控制参数
• 实时分析和合成能力

恒定Q滑动离散傅里叶变换（QDFT）是一种通过逐个样本计算傅里叶变换的递归方法。这是一个没有FFT计算的效率实现。只需定义任意频率范围和八度分辨率，即可获得相应的DFT估计。与线性的SDFT相比，QDFT的频率 bins是对数间隔的。因此，高低频率都可以以相同的质量解析，这对于音频分析特别有用。基于QDFT，计划在未来的版本中添加具有详细瞬时频率估计的音阶图特性。

工作进行中

• README
• 文档字符串
• PyPI软件包 qdft
• Rust软件包
• 作为额外奖励的滑动音阶图（Python软件包中已包含草案）

基本用法

C++

#include <qdft/qdft.h> // see also cpp folder

double sr = 44100;                             // sample rate in hertz
std::pair<double, double> bw = { 50, sr / 2 }; // lowest and highest frequency in hertz to be resolved
double r = 24;                                 // octave resolution, e.g. number of DFT bins per octave

QDFT<float, double> qdft(sr, bw, r); // create qdft plan for custom time and frequency domain data types

size_t n = ...;         // number of samples
size_t m = qdft.size(); // number of dft bins

float* x = ...; // analysis samples of shape (n)
float* y = ...; // synthesis samples of shape (n)

std::complex<double>* dft = ...; // dft matrix of shape (n, m)

qdft.qdft(n, x, dft);  // extract dft matrix from input samples
qdft.iqdft(n, dft, y); // synthesize output samples from dft matrix

默认情况下，时域数据类型为 float，频率域数据类型为 double。

Rust

use qdft::QDFT; // see also rust folder

// just a shortcut for our complex number type
#[allow(non_camel_case_types)]
type c64 = num::complex::Complex<f64>;

// zero number trait, e.g. c64::zero()
use num::Zero;

let samplerate = 44100.0;                 // sample rate in hertz
let bandwidth = (50.0, samplerate / 2.0); // lowest and highest frequency in hertz to be resolved
let resolution = 24.0;                    // octave resolution, e.g. number of DFT bins per octave
let latency = 0.0;                        // analysis latency adjustment between -1 and +1
let window = Some((0.5, -0.5));           // hann window coeffs

// create qdft plan for custom time and frequency domain data types
let mut qdft = QDFT::<f32, f64>::new(
    samplerate,
    bandwidth,
    resolution,
    latency,
    window);

let n = ...;         // number of samples
let m = qdft.size(); // number of dft bins

let mut x = vec![f32::zero(); n]; // analysis samples of shape (n)
let mut y = vec![f32::zero(); n]; // synthesis samples of shape (n)

let mut dft = vec![c64::zero(); n * m]; // dft matrix of shape (n, m)

qdft.qdft(&x, &mut dft);  // extract dft matrix from input samples
qdft.iqdft(&dft, &mut y); // synthesize output samples from dft matrix

或者使用ndarray代替平面数组来分配DFT矩阵，如analysis.rs示例所示。

Python

from qdft import QDFT # see also python folder

sr = 44100        # sample rate in hertz
bw = (50, sr / 2) # lowest and highest frequency in hertz to be resolved
r = 24            # octave resolution, e.g. number of DFT bins per octave

qdft = QDFT(sr, bw, r) # create qdft plan

n = ...       # number of samples
m = qdft.size # number of dft bins (if need to know in advance)

x = ... # analysis samples of shape (n)

dft = qdft.qdft(x)  # extract dft matrix of shape (n, m) from input samples
y = qdft.iqdft(dft) # synthesize output samples from dft matrix

您可以通过执行pip install qdft从PyPI获取当前版本。

示例

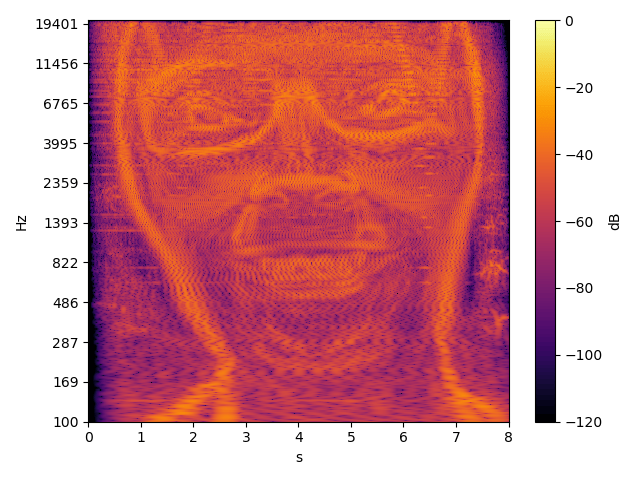
QDFT	Chroma12
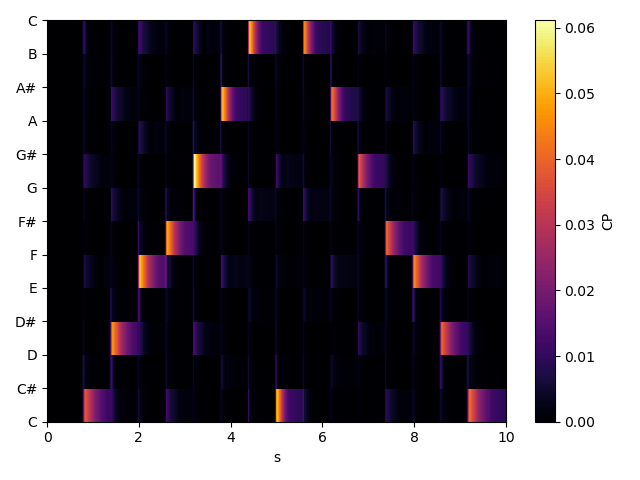face.py	cmajor.py

另请参阅

如果您对具有线性频率分辨率的滑动DFT感兴趣，别忘了浏览我的jurihock/sdft项目！

参考文献

1. Russell Bradford等人（2008年）。恒定Q的滑动。数字音频效果国际会议。https://www.dafx.de/paper-archive/2008/papers/dafx08_63.pdf

2. Bradford 等人（2005年）。滑行比跳跃更平滑。国际计算机音乐会议论文集。http://hdl.handle.net/2027/spo.bbp2372.2005.086

3. Jacobsen 和 Kootsookos（2007年）。快速、精确的频率估计器。IEEE 信号处理杂志。https://ieeexplore.ieee.org/document/4205098

许可证

github.com/jurihock/qdft 采用 MIT 许可证。有关详细信息，请参阅随附的 LICENSE 文件。