10个版本
| 0.3.1 | 2022年7月6日 |
|---|---|
| 0.3.0 | 2022年6月28日 |
| 0.2.0 | 2022年6月27日 |
| 0.1.6 | 2019年10月15日 |
#979 in 算法
340KB
5K SLoC
PLR (分段线性回归)
Rust实现的贪婪和最优误差有界分段线性回归(PLR)算法,这些算法在
Qing Xie, Chaoyi Pang, Xiaofang Zhou, Xiangliang Zhang, and Ke Deng. 2014. Maximum error-bounded Piecewise Linear Representation for online stream approximation. The VLDB Journal 23, 6 (December 2014), 915–937. DOI: https://doi.org/10.1007/s00778-014-0355-0
误差有界分段线性回归是给定一组数据点,找到一个分段线性函数,使得每个数据点在固定范围内近似的任务。有关更多信息,请参阅crate文档。
lib.rs:
此crate提供代码,使用贪婪算法(每点常数时间,常数空间)或最优算法(每点线性时间,线性空间)在线执行误差有界分段线性回归(PLR)。两种算法均按照所述实现。
Qing Xie, Chaoyi Pang, Xiaofang Zhou, Xiangliang Zhang, and Ke Deng. 2014. Maximum error-bounded Piecewise Linear Representation for online stream approximation. The VLDB Journal 23, 6 (December 2014), 915–937. DOI: https://doi.org/10.1007/s00778-014-0355-0
误差界限分段线性回归是这样一个任务:给定一组数据点,找到一个分段线性函数,使其在固定的误差范围内逼近每个数据点。换句话说,对于给定的数据集 (x, y) ∈ D,我们寻求一个分段线性函数 f,使得对于数据集中的每一个 (x, y) ∈ D,都有 |f(x) - y| < δ,其中 δ 是某个给定的值。这也可以被理解为最小化“L-infinity”损失。由于 f 可以通过具有 |D| 个段的分段线性函数简单地实现,因此我们还需要寻找具有最小段数的 f。
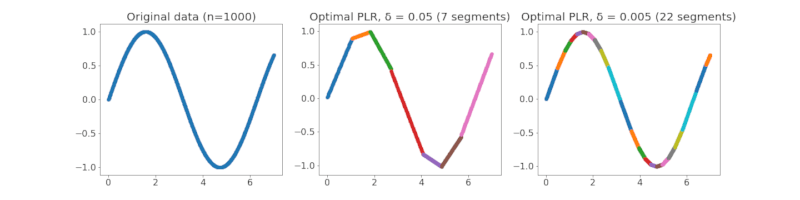
在上面的例子中,我们展示了原始的1000个数据点(左),最大误差为0.05的PLR(中间),以及最大误差为0.005的PLR。所有显示的PLR都是最优的,这意味着它们包含尽可能少的段数以实现其误差界限。
该软件包可以使用两种在线算法之一执行PLR。
- 贪婪PLR,它每个点使用恒定的时间并占用恒定的空间。贪婪PLR总是找到具有指定误差界限的PLR(例如,原始点中的任何一个都不会比其预测值远于 δ),但贪婪方法可能不会找到具有最小段数的PLR。
- 最优PLR,它每个点使用线性时间并可能需要线性空间。在实践中,最优算法使用的空间量应该很小,但最坏情况下可能需要线性空间(参见该论文以获取更多详细信息)。最优算法将找到具有最小段数的解。
该软件包还可以执行样条回归而不是分段线性回归。请参阅greedy_splines或其在线版本GreedySpline。
由Ryan Marcus编写,许可协议为GPL v3。
依赖关系
约4MB
~73K SLoC