3 个版本 (重大更改)
| 0.3.0 | 2024年6月25日 |
|---|---|
| 0.2.0 | 2024年6月10日 |
| 0.1.0 | 2024年3月12日 |
在 算法 中排名第 327
每月下载量 149
84KB
2K SLoC
模块分解
一个用于计算简单无向图模块分解的库。
节点集 M 是一个 模块,如果每个节点在 M 外的邻域都相同。所有节点集 V 和只有一个节点的集合 {u} 是平凡模块。
本库中模块分解算法的运行时间为 O(n + m log n),基于 [HPV99] 和 [CHM02]。尽管存在线性时间算法,但它们的性能较差。
示例
最小的素图是4个节点的路径图。
use petgraph::graph::UnGraph;
use modular_decomposition::{ModuleKind, modular_decomposition};
// a path graph with 4 nodes
let graph = UnGraph::<(), ()>::from_edges([(0, 1), (1, 2), (2, 3)]);
let md = modular_decomposition(&graph)?;
assert_eq!(md.module_kind(md.root()), Some(&ModuleKind::Prime));
确定一个图是否是 cograph。
use petgraph::graph::UnGraph;
use modular_decomposition::{ModuleKind, modular_decomposition};
// a complete graph with 3 nodes
let graph = UnGraph::<(), ()>::from_edges([(0, 1), (0, 2), (1, 2)]);
let md = modular_decomposition(&graph)?;
// a graph is a cograph exactly if none of its modules is prime
let is_cograph = md.module_kinds().all(|kind| *kind != ModuleKind::Prime);
assert!(is_cograph);
// we can also use the method `is_cograph`
assert!(md.is_cograph());
遍历双胞胎、真双胞胎或假双胞胎。
use petgraph::graph::{NodeIndex, UnGraph};
use modular_decomposition::modular_decomposition;
let normalize = |sets: &[Vec<NodeIndex>]| -> Vec<Vec<usize>> {
let mut sets: Vec<Vec<usize>> = sets.iter().map(|nodes| nodes.iter().map(|node| node.index()).collect()).collect();
sets.iter_mut().for_each(|nodes| nodes.sort());
sets.sort();
sets
};
// a K_2 + 2 K_1
let graph = UnGraph::<(), ()>::from_edges([(2, 3)]);
let md = modular_decomposition(&graph)?;
let twins: Vec<_> = md.twins().collect();
assert_eq!(normalize(&twins), [[0, 1], [2, 3]]);
let true_twins: Vec<_> = md.true_twins().collect();
assert_eq!(normalize(&true_twins), [[2, 3]]);
let false_twins: Vec<_> = md.false_twins().collect();
assert_eq!(normalize(&false_twins), [[0, 1]]);
按 DFS 顺序遍历模块分解树。
use petgraph::graph::{NodeIndex, UnGraph};
use modular_decomposition::modular_decomposition;
// some graph
let graph = UnGraph::<(), ()>::from_edges([(2, 3), (3, 4)]);
let md = modular_decomposition(&graph)?;
let mut stack = vec![md.root()];
while let Some(module) = stack.pop() {
stack.extend(md.children(module));
// do something with module
// ...
}
泛型
该算法针对实现 petgraph 特性的结构体实现,包括 NodeCompactIndexable、IntoNeighbors 和 GraphProp<EdgeType = Undirected>。
评估
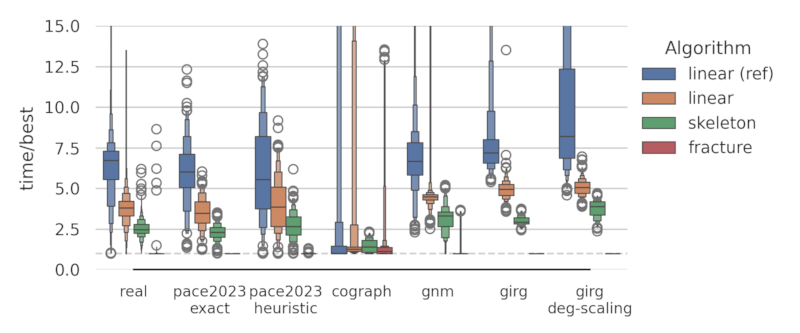
作为论文的一部分,我们评估了四种模块分解算法的实现。性能最佳的 fracture 算法已包含在此库中。有关更多信息,请参阅 仓库。
引用
Jonas Spinner. "模块分解算法的实际评估". https://doi.org/10.5445/IR/1000170363
@mastersthesis{Spinner2024,
doi = {10.5445/IR/1000170363},
url = {https://doi.org/10.5445/IR/1000170363},
title = {A Practical Evaluation of Modular Decomposition Algorithms},
author = {Spinner, Jonas},
year = {2024},
publisher = {{Karlsruher Institut für Technologie (KIT)}},
school = {Karlsruher Institut für Technologie (KIT)},
language = {english}
}
依赖关系
~2.5MB
~35K SLoC