2个版本
使用旧的Rust 2015
| 0.1.1 | 2018年11月16日 |
|---|---|
| 0.1.0 | 2018年11月13日 |
#840 in 数据结构
230KB
1K SLoC
曼哈顿树
曼哈顿树是一种空间树,基于八叉树,允许对元素进行对数时间插入、删除和查询,查询空间中任意点最近元素的曼哈顿距离。
八叉树
这种树的设计基于八叉树。
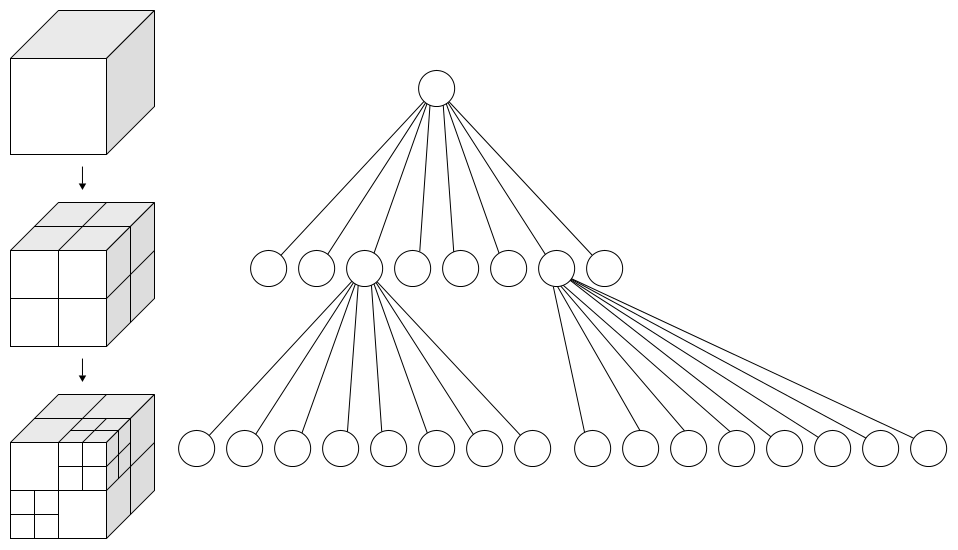
坐标空间的整个域被表示为一个立方体。这个立方体可以递归地分割成8个八分体。
我们引入了两种类型来跟踪这些八分体
- 包含无符号整数坐标的
BaseCoord,[u64; 3]。 - 包含无符号整数坐标的
OctCoord,[u64; 3],以及缩放因子,u8。
有了这些坐标,我们可以定义两种树节点的变体
Leaf,它包含一个BaseCoord和一些树存储的元素Branch,它包含一个OctCoord和8个可选的子Octant
在分支的情况下,在每个维度上,分支的域覆盖从coordinates[n] * (2 pow scale)(包含)到(coordinates[n] + 1) * (2 pow scale)(不包含)的坐标范围。
从这里,我们可以列出一些重要的不变量
- 只有叶子有元素
- 只有分支有子节点
- 一个八分域总是其父域的子域
- 一个分支总是至少有两个子分支
- 一个分支的每个子分支都在分支的不同子八分域中
树缩短
此存储库实现了三维曼哈顿树,但实际上它可以在任何维度工作。以一维曼哈顿树为例。
一个平衡的一维曼哈顿树,包含32个元素,看起来像这样
|----------------------------------------------------------------------------------------------|
|----------------------------------------------||----------------------------------------------|
|----------------------||----------------------||----------------------||----------------------|
|----------||----------||----------||----------||----------||----------||----------||----------|
|----||----||----||----||----||----||----||----||----||----||----||----||----||----||----||----|
|-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-||-|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
一维曼哈顿树的分支因子为 2 pow 1 == 2,并且 log base 2 (32) == 5,因此这个树有5个分支层(不包括根层,或者换句话说,不包括叶层),因此可以认为是效率最高的。
然而,让我们考虑一个元素较少的情况,并且我们错误地处理了这种情况
|----------------------------------------------------------------------------------------------|
|----------------------------------------------||----------------------------------------------|
|----------------------| |----------------------||----------------------|
|----------| |----------||----------|
|----| |----||----|
|-||-| |-| |-|
6 7 22 24
我们已经减少了元素的数量,但我们的树仍然这么高。记住,树的时间复杂度通常取决于其高度。我们希望在保持不变量1和3的同时缩短树
只有叶子有元素
一个八分域总是其父域的子域
此外,这种树结构严重破坏了不变量4
一个分支总是至少有两个子分支
幸运的是,不变量3并不意味着一个八分域的域必须是其父域的直接子域;它可以向下延伸。因此,我们可以通过简单地切断只有一个子分支的分支来缩短树,从而实现不变量4
|----------------------------------------------------------------------------------------------|
|----------------------------------------------||----------------------------------------------|
|-||-| |-| |-|
6 7 22 24
现在,树只有三的高度,每个分支至少有两个子分支。记住,尽管现在更难看到,每个叶子仍然位于其父分支的不同子八分域中。
边界跟踪
我们在每个八分域中包含了一些额外的信息,之前没有提到。对于每个分支,对于每个三个维度,我们编码了存储在完整子树中的整个维度中的最小和最大组件。在向曼哈顿树插入或删除时,必须正确维护这些数据。
曼哈顿距离
给定这些不变量,我们可以高效地执行曼哈顿树的同名操作:找到与任意焦点最近的元素。
焦点是某个任意坐标,就像树中的任何其他键一样。
因此,查找焦点曼哈顿距离最近元素的函数,类似于Rust伪代码,如下所示
fn closest(node: Octant, focus: BaseCoord, competitor: Option<BaseCoord>) -> Option<Leaf>:
if node is a leaf:
return the leaf, unless its mahattan dist (henceforth mdist) to focus is greater
...than the mdist between focus and competitor, if competitor exists
if node is a branch:
// here we take advantage of bounds to short circuit, which is the main performance boost
if competitor exists:
for each of the three dimensions:
let a = competitor.mdist(focus)
let b = the distance in that one dimension between focus, and node's
...closest element to focus, according to the bounds tracking
if a < b:
return None
let best = None
for each child, ordered nearest to furthest from focus:
let child_competitor = {
if best exists: Some(best's coord)
else if competitor exists: Some(competitor)
else: None
}
if let Some(better) = closest(child, focus, child_competitor):
best = Some(better)
return best
位级黑客
许多这些操作,在抽象说明和伪代码中被简化,需要执行坐标操作,例如
OctCoord的哪个子八分域包含特定的BaseCoordOctCoord的哪个子八分域与特定的BaseCoord最接近- 将
OctCoord转换为BaseCoord - 对于两个
BaseCoord是子八分域的最低公共OctCoord是什么
幸运的是,因为底层坐标以无符号二进制整数存储,并且因为每个维度都进行递归二进制细分,可以利用无符号整数的二进制属性,通过位操作实现所有这些操作。这最好用实际代码表达,可以在该crate的 tree/coord 模块中找到。
性能
我在树上进行了性能测试,测试了插入、删除和最接近元素查询,使用不同大小的树。为了最小化外部变量,这些测试在一个从亚马逊EC2租用的 t2.medium 服务器上运行,运行的是Ubuntu服务器18.04。
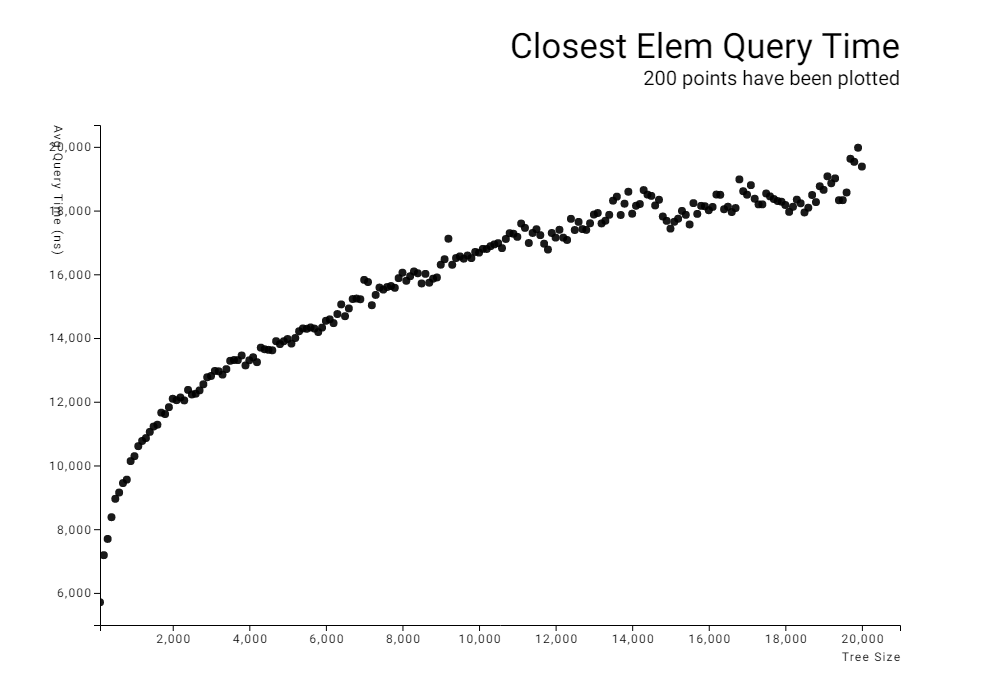
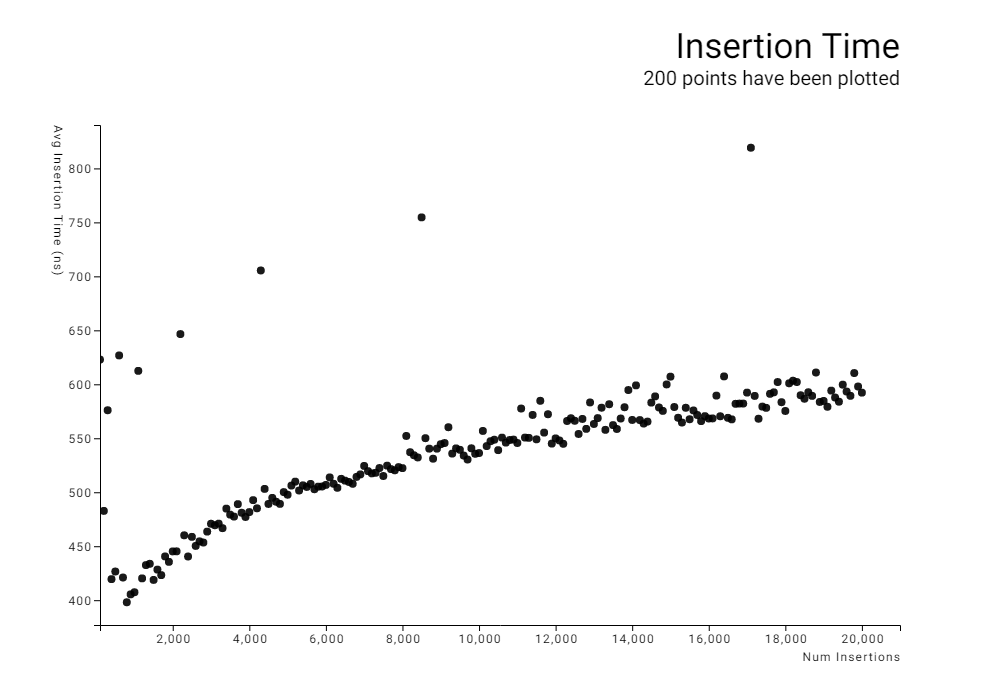
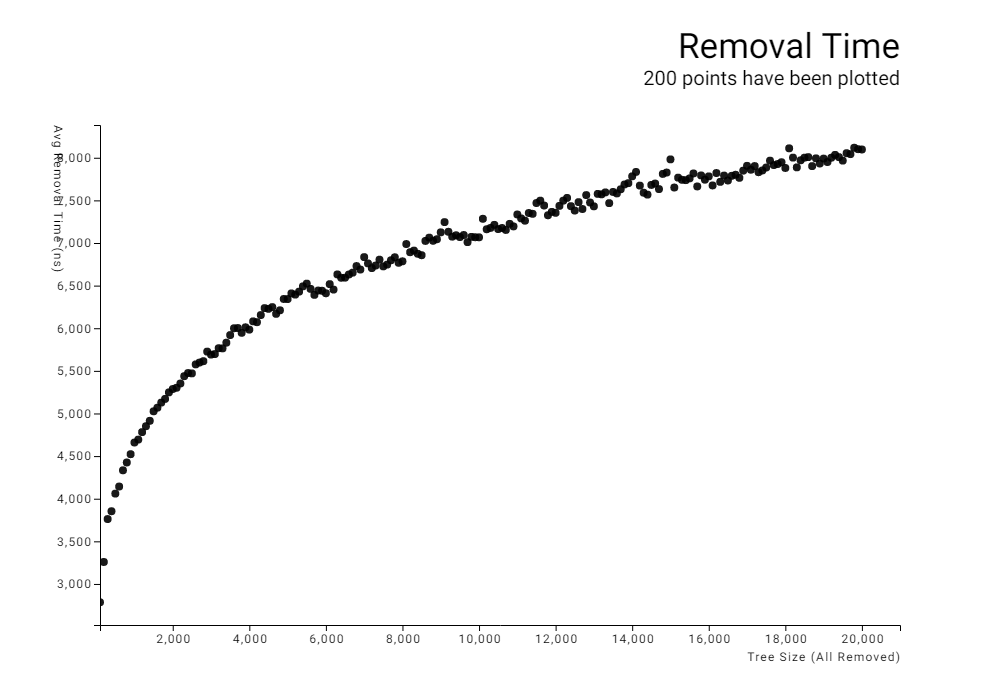
这些结果清楚地显示出对数时间复杂度。进行了一项额外的测试,树的大小达到100,000,我手动将自然对数函数拟合到数据上。
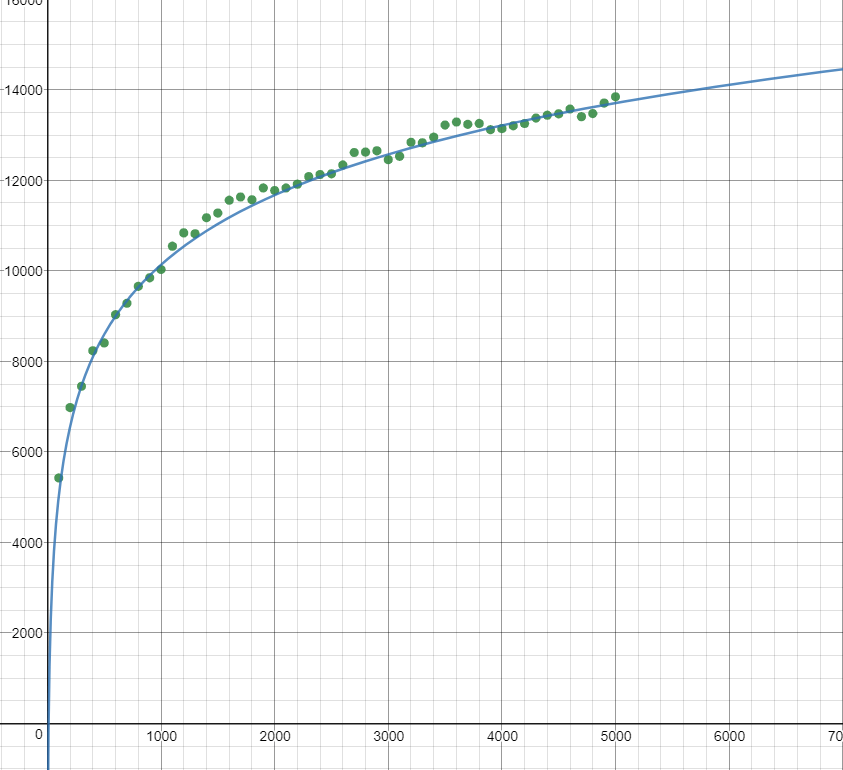
曲线似乎接近以下关系
时间=2220ns* ln(大小) +5200ns
依赖项
~560KB
~11K SLoC