8个版本 (5个破坏性更新)
| 0.6.1 | 2020年12月2日 |
|---|---|
| 0.6.0 | 2020年11月12日 |
| 0.5.0 | 2020年10月5日 |
| 0.4.0 | 2020年9月18日 |
| 0.1.0 | 2020年7月16日 |
#279 in #response
22KB
323 行
冲击响应积分方法
一个用于模拟动态系统,专注于大型稀疏连接系统的工具。
该方法通过测量系统的冲击响应来实现。如果系统是线性和时不变的,则冲击响应完全描述了该系统。可以通过将系统的初始状态与冲击响应卷积来计算系统的确切状态。此方法使用这些事实来解决使用有效稀疏矩阵-向量乘法进行初始值积分问题。
文献
Rotter, S., Diesmann, M. 准确数字模拟时不变线性系统及其在神经元建模中的应用。Biol Cybern 81, 381–402 (1999)。 https://doi.org/10.1007/s004220050570
详细信息
用户使用以下两种方式指定他们的系统
-
状态向量,它完全描述了在某一时刻的系统。
-
状态的导数,作为当前状态的一个函数。
假设用户系统是线性和时不变的。
此方法不允许外部输入。相反,用户应直接修改状态以考虑任何输入。
此方法使用冲击响应以固定的时间步长推进系统状态。首先使用Crank-Nicolson方法和可变长度时间步长,以高保真度计算冲击响应。在冲击后的 time_step 处采样响应。测量每个状态的平均响应并将它们存储在矩阵中。然后为了推进积分状态,将矩阵与状态向量相乘。
冲击响应矩阵是一个方阵,因此其大小是状态向量长度的平方。直观上,这可能会对具有非常大的状态向量的系统造成性能问题。然而,在大多数具有非常大的状态向量的系统中:在测量冲击响应的相对较短的时间步长 time_step 中,大多数状态之间没有相互交互。因此,冲击响应大多是零,冲击响应矩阵可以压缩成稀疏矩阵。
冲击响应积分方法运行速度快,但在启动时需要消耗大量时间和内存来计算和存储冲击响应。
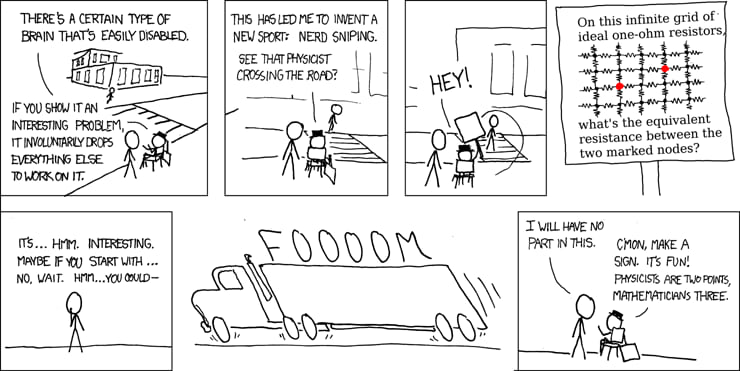
示例:测量等效电阻
这个漫画条提出了一个有趣的问题。这个问题确实有一个已知的解析解,4/pi - 1/2,但也可以使用数值方法进行近似。我演示了如何使用脉冲响应库来完成这个任务。
数值解法
-
首先改变电阻网格的大小,从无限网格到一个非常大的网格。否则就无法计算!因为这个改变,所得的近似值将高估真实值。在极限情况下,当网格大小趋近于无限时,这个高估误差趋近于零。
-
在每个网格节点上连接一个电容器。这模拟了所有导线中存在的寄生电容。为了模拟电荷流动,需要在模型中包含电容。
-
在两个标记节点之间连接一个电压源,并测量通过电压源的电流量。然后使用公式计算等效电阻:
V = I R。由于系统中包含电容器,电流需要时间才能达到稳态。测量稳态电流意味着需要模拟相当长一段时间。
实现和结果
源代码是使用这个库的一个注释示例。链接:impulse_response/examples/nerd_sniping.rs
32x32网格运行代码的结果
$ time cargo run --example nerd_sniping --release
Model Size: 1024 Nodes
Equivalent Resistance: 0.8825786612296072 Ohms
Exact Answer: 4/PI - 1/2 = 0.7732395447351628 Ohms
现在让我们将网格大小增加到633x633,并观察等效电阻更接近正确值。
$ cargo run --example nerd_sniping --release
Model Size: 400689 Nodes
Equivalent Resistance: 0.8416329950362197 Ohms
Exact Answer: 4/PI - 1/2 = 0.7732395447351628 Ohms
运行时间:2天。
测量误差约为8%。
更多示例
tests/leaky_cable.rs
- 模拟神经元树突中的电。
tests/conservation.rs
- 一个人工场景。
- 演示在系统运行时修改系统。
依赖项
~1.5MB
~30K SLoC