3个版本
| 0.1.2 | 2021年12月13日 |
|---|---|
| 0.1.1 | 2019年11月25日 |
| 0.1.0 | 2019年11月16日 |
在 算法 中排名第 516
每月下载 30 次
在 3 crate 中使用
130KB
953 行
希尔伯特曲线变换
Hilbert 库实现了在 Rust 中对二维点的希尔伯特曲线变换及其逆变换的高效 Skilling 算法,最高可扩展到数千维度的点。原始的 C 语言算法可在此会议文章中找到:https://doi.org/10.1063/1.1751381
"Programming the Hilbert curve" by John Skilling. AIP Conference Proceedings 707, 381 (2004);
希尔伯特曲线的用途
研究人员已经发现许多希尔伯特曲线的用途,包括
- 加速K-最近邻搜索
- 无辅助的高维聚类
- 数据压缩
- 伪随机数生成
- 处理激光雷达点云
- 数据库查询优化
- 近似旅行商问题解决方案
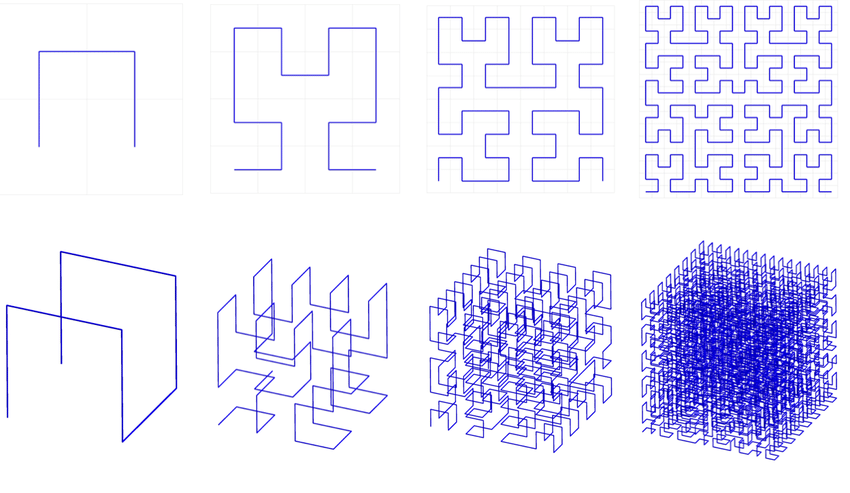
The 1st Three Iterations of the HILBERT CURVE
╔════════════╗ ╔═════╗ ╔═════╗
║ ║ ║ ║ ║ ║
║ ║ ║ ╚════╝ ║
║ ║ ║ ║
║ ║ ╚═════╗ ╔═════╝
║ ║ ║ ║
║ ║ ║ ║
══════╝ ╚══════
1 iteration 2 iterations
╔════╗ ╔════╗ ╔════╗ ╔════╗
║ ║ ║ ║ ║ ║ ║ ║
║ ║ ║ ║ ║ ║ ║ ║
║ ╚════╝ ║ ║ ╚════╝ ║
║ ║ ║ ║
║ ║ ║ ║
╚════╗ ╔════╝ ╚════╗ ╔════╝
║ ║ ║ ║
║ ║ ║ ║
╔════╝ ╚══════════════╝ ╚════╗
║ ║
║ ║
║ ╔═════════╗ ╔═════════╗ ║
║ ║ ║ ║ ║ ║
║ ║ ║ ║ ║ ║
╚════╝ ╔════╝ ╚════╗ ╚════╝
║ ║
║ ║
╔════╗ ╚════╗ ╔════╝ ╔════╗
║ ║ ║ ║ ║ ║
║ ║ ║ ║ ║ ║
║ ╚═════════╝ ╚═════════╝ ║
3 iterations
性能
Skilling 算法可以在与 D(维度数)和B(编码每个坐标所需的位数)成线性比例的时间内执行变换。当处理高维点(超过六个维度)时,这种性能优于文献中的大多数,如果不是所有其他算法。
特性
此库提供以下特性
- 正向希尔伯特曲线变换 从 D 维点到 1 维索引(表示为
BigUint)。请参阅fast_hilbert模块。点可以从两维到数千维。 - 逆向希尔伯特曲线变换 从 1 维
BigUint索引回到 D 维点。请参阅fast_hilbert模块。 - D 维点 的欧几里得距离公式已优化,使其适合用于 K 近邻 搜索。请参阅
Point类。hilbert_sort方法根据希尔伯特曲线对点进行排序。 - 数据归一化 程序,以准备输入数据,使其可以应用希尔伯特变换。请参阅类
IntegerDataRange和FloatDataRange。normalize和compress方法可以将输入数据平移和缩放,并将其强制转换为希尔伯特变换所需的无符号值。 - 排列逻辑,用于生成相同数据的交替希尔伯特曲线。参见
Permutation类。
基准测试
运行基准测试
> cargo bench
基准测试依赖于 criterion crate,如果安装了 gnu-plot 则运行效果最佳。如果已安装且路径中可查找,它将在此处生成报告
hilbert\target\criterion\report\index.html
示例
以下是一些使用此 crate 的示例
- 创建两个 3-D 点并获取它们之间的距离的平方。
- 对单个点执行希尔伯特变换。
- 创建几个点并将它们归一化。
- 按希尔伯特曲线对点进行排序,每个维度使用 11 位。
- 往返,展示如何将点转换为希尔伯特索引然后再转换回来。
// 1. Create two 3-D points and get the square of the distance between them.
let p1 = Point::new(0, &[3, 4, 5]);
let p2 = Point::new(1, &[0, 8, 10]);
let sqr_dist = p1.square_distance(&p2);
assert!(sqr_dist == 50, "Square distance should be 50");
// 2. Perform the Hilbert Transform on a single point,
// using 5 bits per dimension (which assumes no coordinate exceeds 31).
let index1 = p1.hilbert_transform(5);
// 3. Create several points and normalize them.
// This will ensure that the ids begin at zero and that all values
// are multiplied by 10.0 before being rounded to the nearest integer,
// to preserve the predetermined precision.
let point_data : Vec<Vec<f64>> = vec![
vec![-10.5, 5.27, 3.66],
vec![-4.802, 20.2, 100.19],
vec![42.0, -100.0, 0.0]
];
let (mut points, bits) = point_list::make_points_f64(&point_data, 0, None, None, 10.0);
// 4. Sort the points by the Hilbert Curve, using 11 bits per dimension,
// because the range of data is 200.19, multiplied by the scale of 10
// yields 2001.9, ceiling of that yields 2002, which is between 1024 (2^10)
// and 2048 (2^11), so 11 bits are required to store the
// highest coordinate value.
Point::hilbert_sort(&mut points, 11);
// 5. Round trip, from point to Hilbert index and back.
let p1 = Point::new(0, &[3, 4, 5]);
let index = p1.hilbert_transform(5);
let p2 = Point::new_from_hilbert_index(0, &index, 5, 3);
依赖项
~9–20MB
~266K SLoC