7 个版本
| 0.2.10 | 2024年5月28日 |
|---|---|
| 0.2.8 | 2023年10月16日 |
| 0.2.3 | 2023年4月26日 |
| 0.2.2 | 2022年11月10日 |
| 0.1.4 | 2022年10月24日 |
#25 在 科学
42 次每月下载
在 2 个 Crates 中使用(通过 qecp)
1.5MB
23K SLoC
融合之花
量子错误纠正(QEC)的最小权重完美匹配(MWPM)求解器
请参阅我们的教程,以获得快速解释和一些 Python 示例。
我们的论文已在 arXiv 上发表!https://arxiv.org/abs/2305.08307
主要功能
- 正确性:这是一个精确的 MWPM 求解器,经过与 Blossom V 库 的数百万个随机测试用例验证。
- 线性复杂性:在小物理错误率下,平均解码时间大致为 $O(N)$,与缺陷顶点的数量 $N$ 成正比。
- 并行性:单个 MWPM 解码问题可以分割并在并行中解决,然后 融合 以找到精确的全局 MWPM 解。
- 简单接口:图问题被抽象化,对于 QEC 应用易于使用。特别是,它支持解码擦除错误(通过动态设置一些边的权重为 0)。
基准测试亮点
- 在具有 $p$ = 0.001 的电路级噪声模型中,码距 $d$ = 21,旋转 CSS 代码,100000 个测量轮次
- 单线程:每个缺陷顶点 3.9us 或每个测量轮次 13us
- 64-线程:每个缺陷顶点 95ns 或每个测量轮次 0.3us
- 在流模式中,延迟 0.7ms 与测量轮次无关
背景和关键思想
MWPM解码器因其高精度而广为人知,并经过多种优化以进一步提高其精度[1] 和[2]。然而,在过去10年中,关于提高MWPM解码器速度的出版物并不多。Fowler在[3]中实现了一个$O(N)$渐近复杂度的MWPM解码器,并在[4]中提出了一个$O(1)$复杂度的并行MWPM解码器,但据我们所知,这些都没有公开发布。Higgott实现了一个快速但近似的MWPM解码器(即“局部匹配”),其复杂度约为$O(N)$[5]。随着最近在真实硬件上成功实现量子纠错(QEC)的实验,是时候让快速且精确的MWPM解码器对社区开放了。
我们的想法源于我们对Union-Find(UF)解码器[6]的研究。UF解码器是一个具有$O(N)$最坏情况时间复杂度的快速解码器,但与MWPM解码器相比,精度较低。受Fowler的图[3]的启发,我们发现UF解码器之间存在某种关系[7]。这个精彩的动画(按空格键触发动画)可以帮助人们看到UF和MWPM解码器之间的类比。通过这种解释,我们能够结合UF和MWPM解码器的优点。
- 从UF解码器中,我们学会了使用稀疏解码图表示以实现快速速度
- 从MWPM解码器中,我们学会了找到精确的最小权完美匹配以实现高精度
请注意,Oscar Higgott和Craig Gidney独立地提出了使用稀疏解码图以更高效地解决MWPM的相同方法,这在PyMatching V2[8]中得到了体现。他们比融合-绽放(约5倍-20倍的速度提升)具有更好的单线程性能。他们使用了更多优化,如出现在现有文献中的优先队列,这些优化是花朵算法中的(查看他们的论文[9])。此外,他们使用C++语言而不是Rust编程语言。Rust强制执行内存安全,这增加了运行时开销(如向量边界检查和并行编程中的不必要的锁)。我们使用unsafe Rust将速度提高了1.5倍-3倍,但这些特性尚未在Python库中启用,并且仅在原生Rust库中使用时才可用。实际上,PyMatching V2的优化和融合-绽放的并行计算(融合操作)是兼容的。随着他们令人印象深刻的工作,我们期待着并行MWPM解码器速度再提高5倍-20倍。目前,用户应使用PyMatching在大型模拟中实现更好的CPU效率,并使用融合-绽放库作为教育工具,配合可视化工具和入门教程。
演示
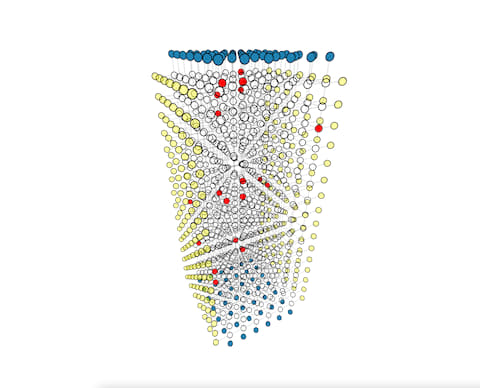
我们强烈建议您观看这里的几个演示,以了解算法的工作原理。我们的所有演示都是从真实算法执行中捕获的。实际上,我们向您展示了我们为融合-绽放编写的可视化调试工具。该演示是一个3D网站,您可以按自己的喜好控制视图点。
点击下面的演示图像以查看相应的演示
串行执行
并行执行(以串行形式显示,以便更好地可视化)
用法
我们的代码是用 Rust 编程语言编写的,以实现速度和内存安全,但这并不是一个容易学习的语言。为了使解码器更易于使用,我们将库与 Python 绑定,用户只需使用以下命令安装库:pip3 install fusion-blossom。
我们在 教程网站 上有多个 Python 示例。还有一个解码器的简单示例,您可以通过克隆项目并运行以下命令来运行它:python3 scripts/demo.py。
对于并行求解器,需要用户提供分区策略。请参阅我们的论文,以详细了解分区的工作原理。
接口
稀疏解码图和整数权重
在 QEC 解码图中,权重是通过计算错误概率的对数来计算的,例如 $w_e = \log{(1-p)/p}$ 或大致 $w_e = -\log{p}$,我们可以通过例如将权重乘以 1e6 并截断到最接近的整数来安全地使用整数来保存权重。这样,整数权重的截断误差 $\Delta w_e = 1$ 对应于相对误差 $\Delta p /{p}=10^{-6}$,这是足够小的。假设物理错误率 $p$ 在一个正的 f64 变量(2.2e-308 到 1)的范围内,最大权重为 7e7,这远远低于 u32 变量的最大值(4.3e9)。由于权重只在我们算法中求和(没有乘法),u32 足够大且足够准确。默认情况下,我们使用 usize,这是与平台相关的(通常是 64 位),但您也可以
我们使用整数是为了更容易迁移到 FPGA 实现。为了将更多顶点放入单个 FPGA,有必要减少每个顶点的资源使用。整数比浮点数便宜得多,并且它还允许在资源使用和精度之间进行灵活的权衡,例如,如果所有权重都相等,我们可以简单地使用 2 位整数。
请注意,MWPM 求解器的其他库(如 Blossom V)也默认使用整数权重。虽然可以更改宏以使用浮点权重,但并不建议这样做,因为“代码甚至可能因为舍入错误而卡住”。
测试
为了测试我们的 MWPM 求解器的正确性,我们需要一个真实情况下的 MWPM 求解器。在现有的 MWPM 解码器中广泛使用的 Blossom V,但根据许可证,我们无法将其嵌入到这个库中。要运行与真实情况比较的测试用例或启用类似 blossom_v_mwpm 的功能,您需要从以下网站下载此库 在此网站 到名为 blossomV 的文件夹中,该文件夹位于 git 仓库的根目录。
wget -c https://pub.ist.ac.at/~vnk/software/blossom5-v2.05.src.tar.gz -O - | tar -xz
cp -r blossom5-v2.05.src/* blossomV/
rm -r blossom5-v2.05.src
可视化
可视化单个解码问题的求解过程
要启动服务器,请运行以下命令
cd visualize
python3 server.py # server
# to view it in a browser interactively, you can run the following command to get url
cd ..
cargo test visualize_paper_weighted_union_find_decoder -- --nocapture
# alternatively, you can choose to render locally
npm install # to download packages
node index.js <url> <width> <height> # local render
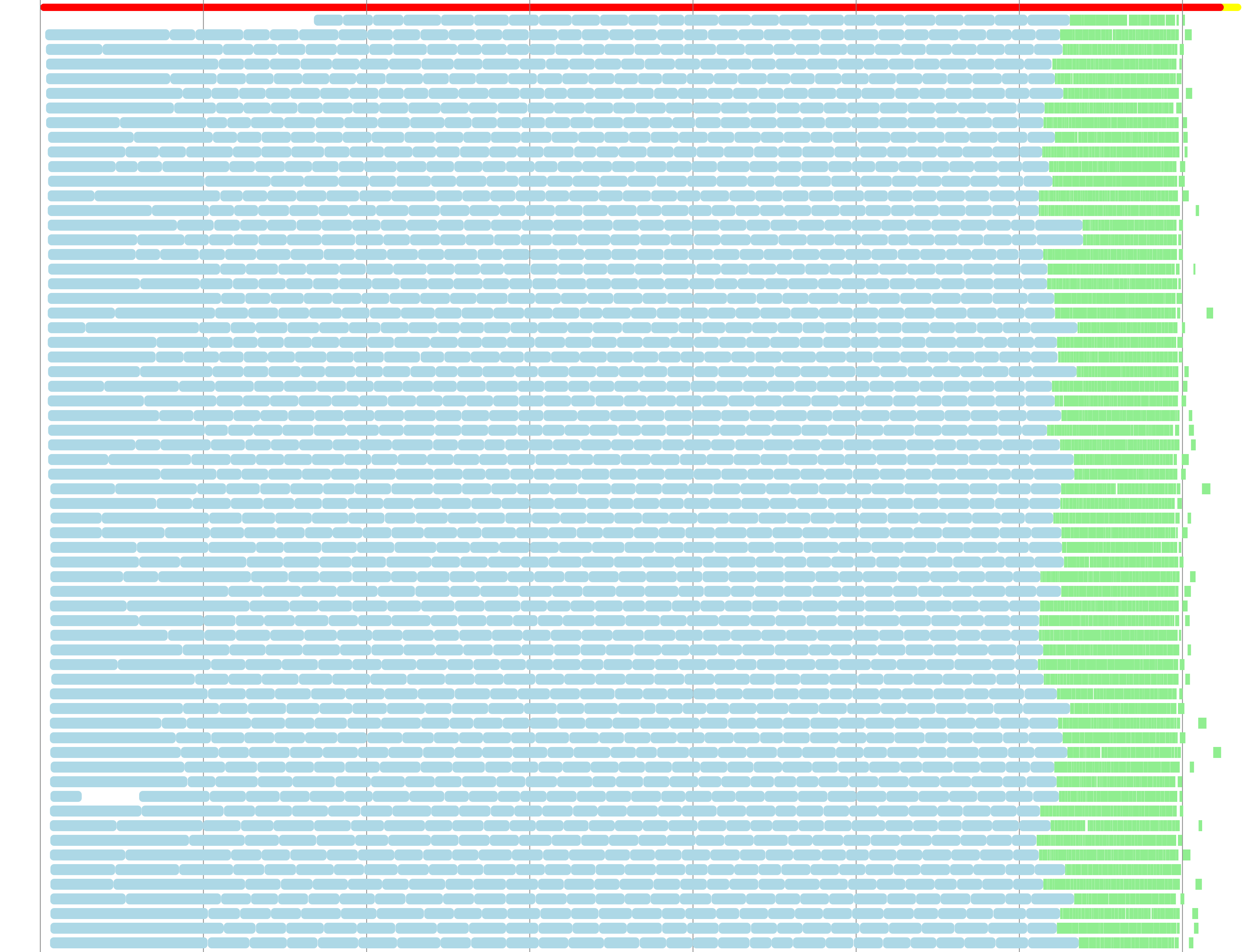
可视化多个解码问题的并行执行
为了理解并行执行的瓶颈,我们编写了一个可视化工具,用于显示多个线程上的基本分区和融合操作的执行窗口。融合操作仅与融合边界的尺寸和活动分区的深度成比例,与基本分区的尺寸无关。我们在论文中研究了不同的分区和融合策略。以下是在 64 个线程上的并行执行。蓝色块是基本分区,每个包含 49 轮测量。绿色块是融合操作,一个轮次测量被两个相邻的基本分区所包围。您可以点击图片,它将跳转到这个交互式可视化工具。
待办事项
- 支持并行求解器中的擦除
致谢
本项目由NSF MRI: Development of PARAGON: Control Instrument for Post NISQ Quantum Computing资助。
参考文献
福勒,奥斯汀·G. 等。 "拓扑代码自调优。" 物理评论X 2.4 (2012): 041003。
克里格,本,和伊姆兰·阿什拉夫。 "用于解码二维拓扑码的多路径求和。" 量子 2 (2018): 102。
福勒,奥斯汀·G.,亚当·C. 怀特赛德,和洛伊斯·C. 霍兰德伯格。 "向表面代码的实用经典处理迈进:时序分析。" 物理评论A 86.4 (2012): 042313。
福勒,奥斯汀·G. "平均 $ O (1) $ 并行时间中容忍故障的拓扑量子纠错的最小权完美匹配。" arXiv预印本arXiv:1307.1740 (2013)。
希戈特,奥斯卡。 "PyMatching:一个用于解码量子码的最小权完美匹配的Python包。" ACM量子计算transactions 3.3 (2022): 1-16。
德尔沃斯,尼古拉,和纳奥米·H. 尼科尔森。 "拓扑码的几乎线性时间解码算法。" 量子 5 (2021): 595。
吴越。 APS 2022年3月会议演讲 "加权图上并查集解码的解释及其在XZZX表面码中的应用"。 演示文稿:https://us.wuyue98.cn/aps2022,视频:https://youtu.be/BbhqUHKPdQk
希戈特,奥斯卡。 PyMatching v2 https://github.com/oscarhiggott/PyMatching
希戈特,奥斯卡,和克雷格·吉丁尼。 "使用最小权匹配每核心每秒纠正一百万个错误:稀疏花簇。" arXiv预印本arXiv:2303.15933 (2023)。
依赖项
~7–20MB
~280K SLoC