我们在以下四个上下文中测试了上述数据类型的散列性能

• hashonly - 仅散列值所需的时间，
• lookupmiss - 在包含随机元素的1,000元素哈希表中查找所需的时间，仅采样我们知道不在哈希表中的键，
• lookuphit - 类似于 lookupmiss，不同之处在于键是从已知存在于哈希表中的键中采样的。
• setbuild - 从1,000个随机采样的元素（每个元素重复10次，因此总共10,000次插入，其中大约90%是重复的）构建包含1,000个元素的 HashSet 所需的时间。

所有时间都是以每操作预期的平均时间为单位，因此分别是：一次哈希、一次查找或一次插入。完整结果 可以在此处找到。为了总结，我们在此只展示针对 u64 和 strenglishword 的结果，以及在整个基准测试中的观察到的几何平均数和平均排名。

Xeon 8481c

┌────────────────┬────────────┬────────────┬────────────┬─────────┬─────────┬─────────┐
│              avg_rank       ┆       1.58 ┆       2.66 ┆    2.09 ┆    3.70 ┆    4.97 │
│        geometric_mean       ┆       6.21 ┆       7.01 ┆    7.56 ┆    8.74 ┆   28.70 │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│          distr ┆      bench ┆ foldhash-f ┆ foldhash-q ┆  fxhash ┆   ahash ┆ siphash │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│            u64 ┆   hashonly ┆       0.79 ┆       1.03 ┆    0.67 ┆    1.23 ┆    9.09 │
│            u64 ┆ lookupmiss ┆       2.01 ┆       2.44 ┆    1.73 ┆    2.73 ┆   12.03 │
│            u64 ┆  lookuphit ┆       3.04 ┆       3.59 ┆    2.64 ┆    3.84 ┆   12.65 │
│            u64 ┆   setbuild ┆       6.13 ┆       6.52 ┆    4.88 ┆    6.66 ┆   17.80 │
|            ... ┆        ... ┆        ... ┆        ... ┆     ... ┆     ... ┆     ... |
│ strenglishword ┆   hashonly ┆       2.63 ┆       2.98 ┆    3.24 ┆    3.57 ┆   11.87 │
│ strenglishword ┆ lookupmiss ┆       4.63 ┆       5.03 ┆    4.51 ┆    5.86 ┆   15.19 │
│ strenglishword ┆  lookuphit ┆       8.62 ┆       9.25 ┆    8.28 ┆   10.06 ┆   21.35 │
│ strenglishword ┆   setbuild ┆      14.77 ┆      15.57 ┆   18.86 ┆   15.72 ┆   35.36 │
└────────────────┴────────────┴────────────┴────────────┴─────────┴─────────┴─────────┘

Xeon 8481c with RUSTFLAGS="-C target-cpu=native"

┌────────────────┬────────────┬────────────┬────────────┬─────────┬─────────┬─────────┐
│              avg_rank       ┆       1.89 ┆       3.12 ┆    2.25 ┆    2.77 ┆    4.97 │ 
│        geometric_mean       ┆       6.00 ┆       6.82 ┆    7.39 ┆    6.94 ┆   29.49 │ 
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│          distr ┆      bench ┆ foldhash-f ┆ foldhash-q ┆  fxhash ┆   ahash ┆ siphash │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│            u64 ┆   hashonly ┆       0.79 ┆       1.01 ┆    0.67 ┆    1.34 ┆    9.24 │
│            u64 ┆ lookupmiss ┆       1.68 ┆       2.12 ┆    1.62 ┆    1.96 ┆   12.04 │
│            u64 ┆  lookuphit ┆       2.68 ┆       3.19 ┆    2.28 ┆    3.16 ┆   13.09 │
│            u64 ┆   setbuild ┆       6.16 ┆       6.42 ┆    4.75 ┆    7.03 ┆   18.88 │
|            ... ┆        ... ┆        ... ┆        ... ┆     ... ┆     ... ┆     ... |
│ strenglishword ┆   hashonly ┆       2.60 ┆       2.97 ┆    3.25 ┆    3.04 ┆   11.58 │
│ strenglishword ┆ lookupmiss ┆       4.41 ┆       4.96 ┆    4.82 ┆    4.79 ┆   32.31 │
│ strenglishword ┆  lookuphit ┆       8.68 ┆       9.35 ┆    8.46 ┆    8.63 ┆   21.48 │
│ strenglishword ┆   setbuild ┆      15.01 ┆      16.34 ┆   19.34 ┆   15.37 ┆   35.22 │
└────────────────┴────────────┴────────────┴────────────┴─────────┴─────────┴─────────┘

Apple M2

┌────────────────┬────────────┬────────────┬────────────┬─────────┬─────────┬─────────┐
│              avg_rank       ┆       1.62 ┆       2.81 ┆    2.02 ┆    3.58 ┆    4.97 │
│        geometric_mean       ┆       4.41 ┆       4.86 ┆    5.39 ┆    5.71 ┆   21.94 │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│          distr ┆      bench ┆ foldhash-f ┆ foldhash-q ┆  fxhash ┆   ahash ┆ siphash │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│            u64 ┆   hashonly ┆       0.60 ┆       0.70 ┆    0.41 ┆    0.78 ┆    6.61 │
│            u64 ┆ lookupmiss ┆       1.50 ┆       1.61 ┆    1.23 ┆    1.65 ┆    8.28 │
│            u64 ┆  lookuphit ┆       1.78 ┆       2.10 ┆    1.57 ┆    2.25 ┆    8.53 │
│            u64 ┆   setbuild ┆       4.74 ┆       5.19 ┆    3.61 ┆    5.38 ┆   15.36 │
|            ... ┆        ... ┆        ... ┆        ... ┆     ... ┆     ... ┆     ... |
│ strenglishword ┆   hashonly ┆       1.84 ┆       2.13 ┆    1.85 ┆    2.13 ┆   11.61 │
│ strenglishword ┆ lookupmiss ┆       2.71 ┆       2.96 ┆    2.47 ┆    2.99 ┆    9.27 │
│ strenglishword ┆  lookuphit ┆       7.54 ┆       8.77 ┆    7.83 ┆    8.77 ┆   18.65 │
│ strenglishword ┆   setbuild ┆      16.61 ┆      17.09 ┆   14.83 ┆   16.52 ┆   26.42 │
└────────────────┴────────────┴────────────┴────────────┴─────────┴─────────┴─────────┘

从上述基准测试中我们可以看出，对于哈希表性能而言，foldhash-q 提供的额外质量几乎从未真正值得它相对于 foldhash-f 的微小但不可忽视的计算开销。这就是我们为什么将 foldhash::fast 作为默认选择提供的原因，尽管它具有可测量的偏差（也请参阅“质量”部分）。

fxhash在基准测试中对小输入通常表现不错，然而作为哈希函数，它具有结构上的弱点，我们认为不建议将其用作通用哈希函数。例如，在Apple M2上针对 u64hibits 的 lookuphit 基准测试中，foldhash的每次查找需要1.77纳秒，而fxhash需要67.72纳秒（由于所有内容都发生冲突 - 如果使用更大的哈希表，效果会更差）。我们认为foldhash-f在质量与性能之间达到了哈希表的正确平衡，而fxhash则过于接近太阳。

当使用AES指令支持编译时，aHash在中等长度的字符串上比foldhash快，但在几乎所有其他情况下或当AES指令不可用时会慢。

质量

foldhash-f在64位完整输出方面是一个相当强的哈希。然而，像SMHasher3这样的统计测试可以区分它和理想哈希函数在关注单个输入/输出位之间关系的测试中。这样的一个属性是雪崩效应：当使用foldhash-f时，输入中的单个比特改变不会以50%的概率翻转另一个比特，这与它像合适的随机预言机那样行为时应发生的相反。

如上述基准测试所示，在foldhash-f上花费更多精力来提高哈希质量并不会导致更好的哈希表性能。然而，也存在一些哈希函数的使用场景，其中每个（比特的）哈希都是无偏的，并且是输入中所有比特的随机函数，例如在HyperLogLog或MinHash等算法中。

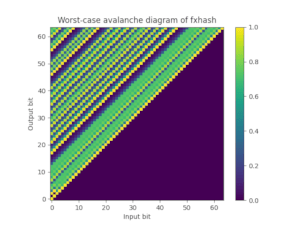
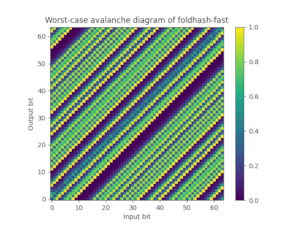
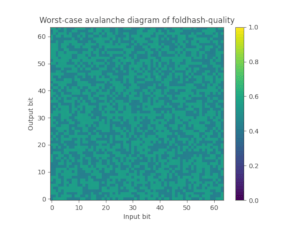
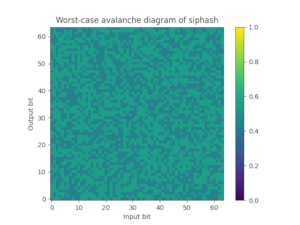
为此，我们还提供了foldhash-q，它只是foldhash-f的后处理版本，以正确地雪崩所有比特。Foldhash-q通过了 SMHasher3 测试套件 没有任何失败。您还可以绘制翻转输入比特时翻转特定输出比特的极端概率（50%是理想的），这可以很好地展示fxhash和foldhash-f如何失败这个雪崩属性，而foldhash-q和SipHash-1-3如何通过。

FxHash	Foldhash-f	Foldhash-q	SipHash-1-3

背景

foldhash这个名字来源于折叠乘法技术。这种方法将两个64位单词压缩成一个64位单词，同时充分混合比特。它通过64 x 64位 -> 128位的乘法来实现，然后使用XOR操作将128位乘积的两个半部分折叠在一起。

let full = (x as u128) * (y as u128);
let lo = full as u64;
let hi = (full >> 64) as u64;
let folded = lo ^ hi;

我们不知道有关于这种操作形式的正式分析，但根据经验，它工作得非常好。为什么它应该有效的一个非正式的直观理解是，乘法可以看作是一个参数的多个平移副本的和，只包括另一个参数中设置了位的那些平移副本，例如，对于乘以4位字 abcd 和 efgh

abcd * efgh =

  abcd    * e
   abcd   * f
    abcd  * g
     abcd * h
--------------- +

请注意，乘积的中间位是许多输入位的一个函数，而最高位和最低位受较少的输入位的影响。通过将上半部分折叠回下半部分，这些影响相互补偿，使得所有输出位都受到大部分输入位的影响。

我们并非发明了折叠乘法，它以前以基本上相同的方式在 aHash，wyhash 和 xxhash3 中使用过。该操作也用于 mum-hash，以及可能的其他地方。我们不知道谁最初发明了它，我们能找到的最早参考文献是 Steven Fuerst 在 2012 年 撰写关于它的博客。

抗哈希拒绝服务（HashDoS）

折叠乘法有一个相当明显的缺陷：如果一个半部分是零，输出就是零。这使得创建大量的哈希冲突变得容易（甚至可能是偶然的，因为零是哈希的常见输入）。为了应对这个问题，foldhash 中的每个折叠乘法都有以下形式

folded_multiply(input1 ^ secret1, input2 ^ secret2)

在这里，secret1 或 secret2 要么是 foldhash 事先生成的秘密随机数，要么是受此类秘密影响的部分哈希结果。这（加上哈希函数中的其他精心设计）确保了不可能创建一个输入列表，该列表在 foldhash 的每个实例中都发生冲突，并且还通过确保每个哈希表使用不同的种子和因此不同的访问模式，防止了哈希表上的某些访问模式成平方增长。当我们声称 foldhash 是“最小化 DoS-抵抗的”时，我们指的是这两个属性：它做了最小的工作来击败非常简单的攻击。

然而，为了清楚起见，foldhash 不声称能抵御交互式攻击者的哈希拒绝服务（HashDoS）。对于密码学的学生来说，从直接观察哈希输出中推导出秘密值应该是显而易见的，从间接观察哈希（例如通过时间攻击或哈希表迭代）中推导出秘密值也是可行的。一旦攻击者知道了秘密值，他们就可以再次轻松地创建无限多的哈希冲突。