5 个不稳定版本
使用旧的 Rust 2015
| 0.4.2 | 2018 年 11 月 3 日 |
|---|---|
| 0.4.1 | 2018 年 11 月 3 日 |
| 0.4.0 | 2018 年 10 月 13 日 |
| 0.2.1 | 2018 年 9 月 1 日 |
| 0.1.0 | 2018 年 8 月 3 日 |
#78 in 解析工具
29 每月下载量
160KB
2K SLoC
DynParser
一个小巧简单的动态解析器。它不是编译时解析器。
您可以在运行时创建和修改语法。
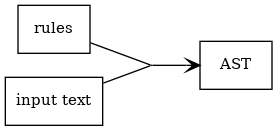
解析器是一种接受 input,用一些 rules 处理它并生成一个 AST 的东西
还有一些工具可以管理 AST(修剪、压缩、展平等)
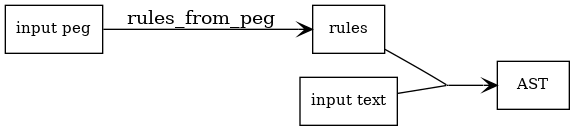
为了创建语法,您可以构建一组规则,或者您可以使用宏来使用更好的语法。但是,最简单的方法是使用 peg 语法。
然后我们需要一个额外的步骤。
下面是有关 peg 语法的更多信息。
您还可以从 peg 生成的规则生成 rust 代码。
这允许您避免 peg 步骤以及更多...
实际上,为了使用 peg 语法,您必须解析它。如何解析 peg 语法?嗯,这是一个解析器,因此...
下面将在(解析解析器)部分提供更多详细信息。
用法
添加到 cargo.toml
[dependencies]
dynparser = "0.4.0"
查看下面的示例
修改
0.1.0 First version
0.2.0 Fixed some errors
Rules code for peg parsing generated automatically from peg
0.3.0 Passthrow method on AST
0.4.0 Literals with escape (optional)
Error constructor on peg grammar
Flattening the AST
0.4.2 Fixed error managing error("xxx")
Working on modules
待办事项
- 通过示例 2.0 将其移动到宏并改进一些
- 应用尾递归解析规则
- eof 的宏
基本示例
让我们创建下一个语法
main = letter letter_or_num+
letter = [a-zA-Z]
letter_or_num = letter
/ number
number = [0-9]
这个语法将接受一个字母,后面跟一个或多个字母或数字
仅从 peg

简单...
extern crate dynparser;
use dynparser::{parse, rules_from_peg};
fn main() {
let rules = rules_from_peg(
r#"
main = letter letter_or_num+
letter = [a-zA-Z]
letter_or_num = letter
/ number
number = [0-9]
"#,
).unwrap();
assert!(parse("a2AA456bzJ88", &rules).is_ok());
}
如果您想打印更多信息...
extern crate dynparser;
use dynparser::{parse, rules_from_peg};
fn main() {
let rules = rules_from_peg(
r#"
main = letter letter_or_num+
letter = [a-zA-Z]
letter_or_num = letter
/ number
number = [0-9]
"#,
).map_err(|e| {
println!("{}", e);
panic!("FAIL");
})
.unwrap();
println!("{:#?}", rules);
let result = parse("a2Z", &rules);
match result {
Ok(ast) => println!("{:#?}", ast),
Err(e) => println!("Error: {:?}", e),
};
}
生成的 AST 将是
Rule(
(
"main",
[
Rule(
(
"letter",
[
Val(
"a"
)
]
)
),
Rule(
(
"letter_or_num",
[
Rule(
(
"number",
[
Val(
"2"
)
]
)
)
]
)
),
Rule(
(
"letter_or_num",
[
Rule(
(
"letter",
[
Val(
"Z"
)
]
)
)
]
)
)
]
)
)
AST 类型是
pub enum Node {
Val(String),
Rule((String, Vec<Node>)),
EOF,
}
您还可以处理扁平化的 AST。在许多情况下,访问扁平化的 AST 会更简单。
扁平化的 AST 是
pub enum Node {
Val(String),
BeginRule(String),
EndRule(String),
EOF,
}
}
就是这样(记住,关于 peg 语法的更多信息见下文)
示例 2
您将配置一组要解析的规则。
规则由一个名称、一个箭头和一个待解析的表达式组成。
基本示例
让我们创建下一个语法
main = 'a' ( 'bc' 'c'
/ 'bcdd'
/ b_and_c d_or_z
)
b_and_c = 'b' 'c'
d_or_z = 'd' / 'z'
仅从第2个图钉开始
extern crate dynparser;
use dynparser::{parse, rules_from_peg};
fn main() {
let rules = rules_from_peg(
r#"
main = 'a' ( 'bc' 'c'
/ 'bcdd'
/ b_and_c d_or_z
)
b_and_c = 'b' 'c'
d_or_z = 'd' / 'z'
"#,
).unwrap();
assert!(parse("abcz", &rules).is_ok());
assert!(parse("abcdd", &rules).is_ok());
assert!(parse("abcc", &rules).is_ok());
assert!(parse("bczd", &rules).is_err());
}
出口将是下一个AST
Rule(
(
"main",
[
Val(
"a"
),
Rule(
(
"b_and_c",
[
Val(
"b"
),
Val(
"c"
)
]
)
),
Rule(
(
"d_or_z",
[
Val(
"d"
)
]
)
)
]
)
)
这是一个动态解析器,您可以在执行时添加规则。
待定:示例
使用宏手动生成规则
您可以使用宏创建此语法并解析字符串“abcd”,如下所示
#[macro_use]
extern crate dynparser;
use dynparser::parse;
fn main() {
let rules = rules!{
"main" => and!{
lit!("a"),
or!(
and!(lit!("bc"), lit!("c")),
lit!("bcdd"),
and!(
ref_rule!("b_and_c"),
ref_rule!("d_or_z")
)
)
},
"b_and_c" => and!(lit!("b"), lit!("c")),
"d_or_z" => or!(lit!("d"), lit!("z"))
};
let result = parse("abcd", &rules);
match result {
Ok(ast) => println!("{:#?}", ast),
Err(e) => println!("Error: {:?}", e),
};
}
在执行时添加规则
#[macro_use] extern crate dynparser;
use dynparser::parse;
fn main() {
let rules = rules!{
"main" => and!{
rep!(lit!("a"), 1, 5),
ref_rule!("rule2")
}
};
let rules = rules.add("rule2", lit!("bcd"));
assert!(parse("aabcd", &rules).is_ok())
}
当然,您可能需要一次性添加(或合并)多个规则
当然,您可以一次性添加多个规则
#[macro_use] extern crate dynparser;
use dynparser::parse;
fn main() {
let r = rules!{
"main" => and!{
rep!(lit!("a"), 1, 5),
ref_rule!("rule2")
}
};
let r = r.merge(rules!{"rule2" => lit!("bcd")});
assert!(parse("aabcd", &r).is_ok())
}
merge 接管两组规则的所有权并返回一个“新”(实际上是修改后的)规则集。这有助于减少可变性
main 规则是入口点。
更多信息请参阅文档
计算器示例
没有基本数学表达式解析器示例,解析器就不是解析器。
下面是...
extern crate dynparser;
use dynparser::{parse, rules_from_peg};
fn main() {
let rules = rules_from_peg(
r#"
main = _ expr _
expr = add_t (_ add_op _ add_t)*
/ portion_expr
add_t = fact_t (_ fact_op _ fact_t)*
fact_t = portion_expr
portion_expr = '(' expr ')'
/ item
item = num
num = [0-9]+ ('.' [0-9]+)?
add_op = '+' / '-'
fact_op = '*' / '/'
_ = ' '*
"#,
).map_err(|e| {
println!("{}", e);
panic!("FAIL");
})
.unwrap();
let result = parse(" 1 + 2* 3 +(5/5 - (8-7))", &rules);
match result {
Ok(ast) => println!(
"{:#?}",
ast.compact()
.prune(&vec!["_"])
.passthrow_except(&vec!["main", "add_t", "fact_t"])
),
Err(e) => println!("Error: {:?}", e),
};
}
PEG
规则元素枚举
以下示例
| 标记 | 描述 |
|---|---|
= |
在左侧,符号;在右侧定义符号的表达式 |
符号 |
它是一个不带引号的字符串 |
. |
任何字符 |
'...' |
由单引号分隔的文本 |
"..." |
由引号分隔的文本。它接受转义字符 |
空格 |
分隔标记和规则连接(和操作) |
/ |
或操作 |
(...) |
由子表达式组成的表达式 |
? |
一个可选的 |
* |
重复0次或更多 |
+ |
重复1次或更多 |
! |
否定表达式 |
[...] |
匹配字符。它是一个列表或范围(或两者都是) |
错误(...) |
让我们定义特定错误 |
-> |
待定... |
: |
待定... |
让我们通过示例看看
示例规则
了解PEG语法的最好方法是查看PEG语法。是的,它就在PEG语法中 :-)
一个简单的文本字符串。
main = 'Hello world'
有两种文本类型。
没有转义文本,由'分隔
转义文本,由"分隔。例如,"\n"将转换为换行符,即。
可以用十六进制数表示一个字符。例如,"0x13"
main = "Hello\nworld"
main = "Hello\0x13world"
main = 'Hello' "\n" 'world'
main = 'Hello' "\0x13" 'world'
使用这两种类型的文本,很容易有"和'
main = "'"
main = '"'
建议尽可能使用非转义文本,并在必要时使用转义文本。
连接(和)
main = 'Hello ' 'world'
引用符号(规则)
符号
main = hi
hi = 'Hello world'
或/
main = 'hello' / 'hi'
或多行
main
= 'hello'
/ 'hi'
/ 'hola'
或多行2
main = 'hello'
/ 'hi'
/ 'hola'
或无序
main = 'hello'
/ 'hi' / 'hola'
关于or的一个重要注意事项
main = 'hello'
/ 'hello world'
/ 'hola'
给定文本hello world,第一个选项将匹配处理输入的第一个单词,而第二个选项将永远不会被执行。这可以修复,但...看起来不是一个好主意。
修复语法以避免这种问题很容易。尝试修复解析器以允许这种类型的语法,代价很高。
括号
main = ('hello' / 'hi') ' world'
仅多行
多行1
main
= ('hello' / 'hi') ' world'
多行2
main
= ('hello' / 'hi')
' world'
多行3
main = ('hello' / 'hi')
' world'
建议在每个新行上使用或操作符/,并在第一行上使用=,如下所示
多行有序
main = ('hello' / 'hi') ' world'
/ 'bye'
一个可选的
main = ('hello' / 'hi') ' world'?
重复
main = one_or_more_a / zero_or_many_b
one_or_more = 'a'+
zero_or_many = 'b'*
否定不会移动当前位置
下一个示例将消费所有字符,直到得到一个'a'。
否定
main = (!'a' .)* 'a'
消费直到
// This is a line comment
/* This is a
multiline comment */
comment = '//' (!'\n' .)* // line comment can be at the end of line
/ '/*' (!'*/' .)* '*/' /* a multiline comment can start
at any place
*/
匹配一组字符。字符可以通过范围定义。
number = digit+ ('.' digit+)?
digit = [0-9]
a_or_b = [ab]
id = [_a-zA-Z][_a-zA-Z0-9]*
a_or_b_or_digit = [ab0-9]
简单递归
一个或多个'a'递归
as = 'a' as
/ 'a'
// simplified with `+`
ak = 'a'+
递归匹配括号
递归匹配par
match_par = '(' match_par ')'
/ '(' ')'
这很好,但我们可以改进错误消息...
为了改进错误消息,修改语法会很有趣。
见下一节。
在某些情况下,我们可能会遇到一个错误,因为它不会终止地消费完整输入。
原因在于
...
and_expr = compl_expr ( ' ' _ and_expr)*
...
显示一个错误,告知我们没有消费完整输入,并不是最好的。
在这里,我们说,“嘿,尝试查找一个序列,或者不是 *”
如果不是,解析器会说,我匹配了规则,我必须继续验证其他先前分支。但是没有先前部分应用的分支。然后解析器结束,没有消费所有输入。
为了改进错误消息,有趣的是有像这样的东西
错误包括在peg语法中也将有助于这种情况(见下一节)
下面的peg格式中的完整语法(一个语法的语法)...
错误
错误非常重要。
看看这个语法
main = '(' main ')'
/ 'hello'
它将强制匹配单词'hello'周围的括号
那很好,但如果我们写 ((hello)
系统会指出错误位置,但...消息会是什么?
我们希望得到一个像 unbalanced parenthesis 的消息
我们可以...
main = '(' main ( ')' / error("unbalanced parenthesis") )
/ 'hello'
使用这个构造函数,我们可以改进我们的错误消息 :-)
我们还可以删除类似于 not consumed full input 的错误
记住。了解peg语法的最好方法是查看peg语法。是的,它就在peg语法中 :-)
完整的示例...
extern crate dynparser;
use dynparser::{parse, rules_from_peg};
fn main() {
let rules = rules_from_peg(
r#"
main = '(' main ( ')' / error("unbalanced parenthesis") )
/ 'hello'
"#,
).unwrap();
match parse("((hello)", &rules) {
Ok(_) => panic!("It should fail"),
Err(e) => assert!(e.descr == "unbalanced parenthesis"),
}
}
文本
嘿,我是一个文本解析器,我需要一个文本来解析 ;-P
如果您想解析对缩进敏感的文本,我推荐您使用库 indentation_flattener
语法的语法
定义解析器将要解析的语法的语法。 ;-P
我将使用这个解析器语法定义规则来定义语法。
一个语法是一组规则。
一个规则是一个符号后跟 = 和一个表达式
grammar = rule+
rule = symbol '=' expr
在这里,我们放宽了验证,以使语法尽可能简单。它也缺少非重要空格。
关于表达式。
正如您所知,接受有效输入很重要,但构建具有适当优先级的AST也很重要。
下一个语法
main = 'A' 'B' / 'B' 'C'
它相当于
main = ('A' 'B') / ('B' 'C')
但不相当于
main = (('A' 'B') / 'B') 'C'
为了表示这种优先级,表达式规则必须按子代优先级方式定义
expr = or_expr
or_expr = and_expr ('/' or_expr)*
and_expr = simpl_expr (' ' and_expr)*
simpl_expr = '!' atom_or_par
/ simpl_par ('*' / '+')
atom_or_par = (atom / parenth_expr)
parenth_expr = '(' expr ')'
子代定义
| expr | 描述 |
|---|---|
| atom_or_par | 它是一个原子或括号表达式 |
| rep_or_neg | 它不是一个由 and 或 or 表达式组成的组合。它可以有否定或重复 |
| parenth | 它是一个带括号的表达式 |
| and | 通过空格分隔的表达式序列 |
| or | 通过 '/' 分隔的表达式序列 |
现在,轮到 atom 了
atom = literal
/ match
/ dot
/ symbol
literal = "\"" (!"\"" .)* "\""
match = '[' ((. '-' .) / (.))+ ']'
dot = '.'
symbol = [a-zA-Z0-9_]+
关于注释怎么办?
关于非重要空格和回车怎么办?
它将在 '_' 符号上定义
这是总体思路。解析器使用的peg将演变为添加错误控制、变量、字符串中的转义符以及其他想法。
由于解析器将从 peg 生成代码来自我解析... 因此,保持用于从 peg 解析的 peg 语法更新很容易。
main = grammar
grammar = rule+
rule = _ symbol _ '=' _ expr _eol _
expr = or
or = and ( _ '/' _ or )*
and = rep_or_neg ( _1 _ !(symbol _ '=') and )*
rep_or_neg = atom_or_par ('*' / '+' / '?')?
/ '!' atom_or_par
atom_or_par = (atom / parenth)
parenth = '(' _ expr _ ')'
atom = literal
/ match
/ dot
/ symbol
literal = lit_noesc / lit_esc
lit_noesc = _' ( !_' . )* _'
_' = "'"
lit_esc = _"
( esc_char
/ hex_char
/ !_" .
)*
_"
_" = '"'
esc_char = '\r'
/ '\n'
/ '\\'
/ '\"'
hex_char = '\0x' [0-9A-F] [0-9A-F]
symbol = [_a-zA-Z0-9] [_'"a-zA-Z0-9]*
eol = ("\r\n" / "\n" / "\r")
_eol = ' '* eol
match = '['
(
(mchars mbetween*)
/ mbetween+
)
']'
mchars = (!']' !(. '-') .)+
mbetween = (. '-' .)
dot = '.'
_ = ( ' '
/ eol
)*
_1 = (' ' / eol)
解析解析器
或者... 如何解析自己
记住,我们是从简单的解析器概念开始的...
从一组规则和要处理的输入开始,我们将生成 AST

在此基础上,我们添加了一个额外步骤,从 peg 语法 生成规则,避免手动编写代码。
然后,我们有一个接受 peg 语法的解析器。
现在,我们不再提供规则集,而是可以提供一个 peg 定义和输入来生成 AST

但是,必须处理(解析)输入 peg 语法。我们必须编写 rules_from_peg 代码来解析 输入 peg
谁将解析语法 peg?一个解析器?
让我想想... 嗯嗯!!!
我就是解析器!!!
我们有一个功能,可以生成从 peg 语法生成的 AST 树的 Rust 代码。哦?!
所以,解析 peg 语法的代码将自动由这个解析器生成

然后我们将自动递归地生成 rules_from_peg
完成这些后,我们现在可以以经典方式使用解析器
记住,正常的解析,我们有两个输入。
peg 语法- 输入文本
现在,首先,两个输入都将是一个定义自身的 peg 语法(一个 peg 语法 定义一个 peg 语法)
- 输入:定义自身的
peg 语法 - 运行
rules_from_peg以为这个peg 语法生成一组规则 - 通过这两点,我们将解析创建
peg 语法的AST - 现在我们将调用
ast::generate_rust来生成rules_from_peg的代码 - 我们将把这段代码插入到解析器中
- 然后我们可以用
peg 语法解析输入,以生成AST
点 rules_from_peg 很特殊。
pub fn rules_from_peg(peg: &str) -> Result {
let ast = parse(peg, &rules::parse_peg())?;
let nodes = ast.compact().prune(&["_", "_1", "_eol"]).flatten();
rules_from_flat_ast(&nodes)
}
如您所见,我们解析了 peg 语法(在这种情况下是一个定义 peg 语法的 peg)。
然后,我们通过压缩、删除节点和扁平化来转换 AST。
一个扁平化的 AST 只是需要解析的东西,但我们用标记而不是字符工作,它是一个 LL(1) 解析器。
错误将在之前的解析中找到并注册。
然后,我们必须手动编写 LL(1) 解析器,但这很容易(不需要控制错误,不处理字符,只是 LL(1))
为什么要这样做?
首先,这是可能的,并且是一个很好的测试。
其次。如果我们想修改我们的 peg 语法,手动编写代码既无聊又容易出错。
使用 peg 文件自动生成 rules_from_peg,使文档和代码保持同步(始终同步)
图表生成
echo "[ input peg ] -- rules_from_peg --> [ rules ][ input text ], [ rules ] --> { end: back,0; } [ AST ]" | graph-easy --dot | dot -Tpng -o doc_images/basic.png
echo "[ rules ][ input text ], [ rules ] --> { end: back,0; } [ AST ]" | graph-easy --dot | dot -Tpng -o doc_images/simple_parser.png
echo "
[input peg \\n
for peg grammar ] -- [rules_from_peg] { shape: none; } -->
[rules_peg_gramm] { label: rules\\n
for peg grammar }
[input peg \\n
for peg grammar ], [ rules_peg_gramm ] -- parse --> { end: back,0; } [ AST ]
[AST] ~~ generate rust ~~> [rules_from_peg] { shape: none; }
" | graph-easy --dot | dot -Tpng -o doc_images/automatic_diagram.png