7个版本 (3个稳定版本)
使用旧Rust 2015
| 1.0.2 | 2022年6月19日 |
|---|---|
| 1.0.1 | 2020年10月25日 |
| 1.0.0 | 2018年7月18日 |
| 0.1.3 | 2017年5月8日 |
| 0.1.1 | 2017年1月6日 |
#318 in 算法
15,517 每月下载量
用于 31 个crate(5个直接使用)
20KB
263 行
摘要
这是一个针对几乎有序数据的自适应排序算法实现。DM排序特别适用于80%以上的数据已经有序且无序元素分布均匀的情况。一个示例用例是在对已排序列表进行少量修改后重新排序。
当排序长列表(10k元素或更多)且80%以上的数据已经有序时,DM排序比quicksort快2-5倍,而其实现比其他自适应排序算法简单得多。
当列表中有N个元素,其中K个元素是无序的,DM排序进行 O(N + K⋅log(K)) 比较和使用 O(K) 额外内存。
定义:如果最长非递减子序列包含X%的元素,则X%的元素是有序的。
开始使用crate
将其添加到 Cargo.toml
[dependencies]
dmsort = "1.0.0"
然后使用它
extern crate dmsort;
fn main() {
let mut numbers : Vec<i32> = vec!(0, 1, 6, 7, 2, 3, 4, 5);
dmsort::sort(&mut numbers);
assert_eq!(numbers, vec!(0, 1, 2, 3, 4, 5, 6, 7));
}
性能
为了测试此算法的性能,我生成了类似这样的几乎有序数据(伪代码)
function generate_test_data(length, disorder_factor) -> Vec {
result = Vec::new()
for i in 0..length {
if random_float() < disorder_factor {
result.push(random_integer_in_range(0, length))
} else {
result.push(i)
}
}
return result
}
然后,我对Drop-Merge排序与以下算法进行了基准测试
- 默认Rust排序算法(《Vec::sort》,一个基于Timsort的稳定排序算法)
- pdqsort(模式破坏quicksort)
- quickersort(双轴quicksort)
基准测试是在2013年早期MacBook Pro Retina上使用rustc 1.15.0 (10893a9a3 2017-01-19)。
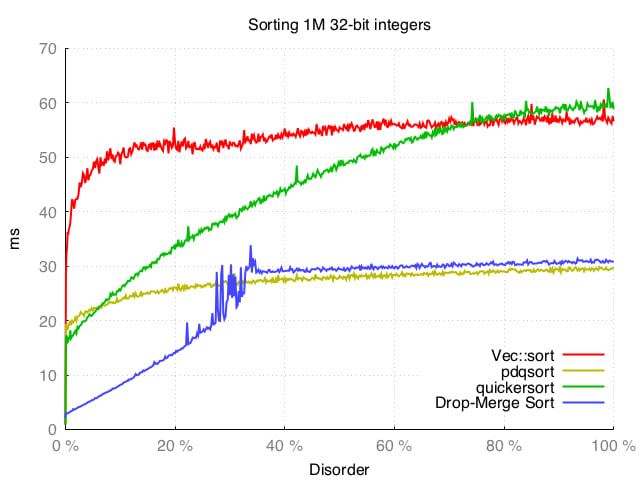
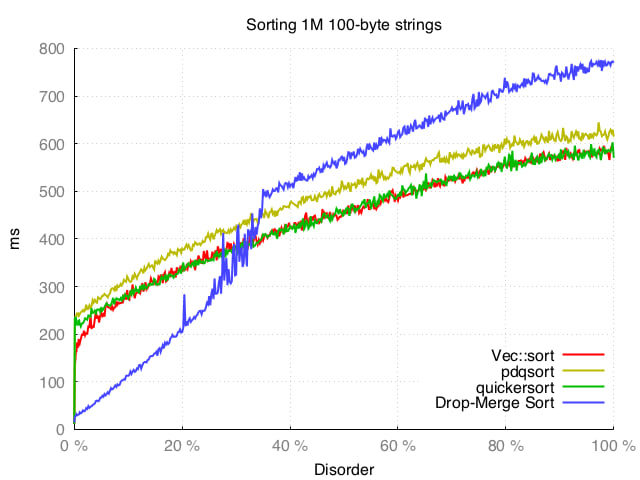
我们可以看到,所有四种算法都能够处理几乎排序好的数据,但当无序因素低于30%(超过70%的元素是有序的)时,Drop-Merge排序更具优势。
当数据变得更加随机时,它表现良好,在最糟糕的情况下,它仍然只比pdqsort慢大约30%(pdqsort是Drop-Merge排序的回退选项)。
以下是0-50%无序数据的数据视图
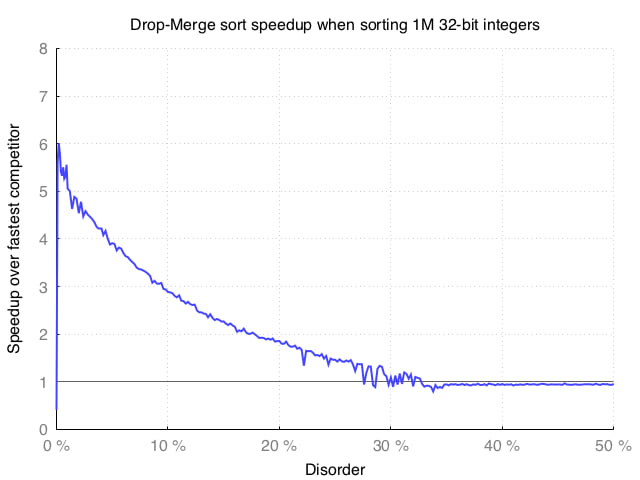
在这里,我们可以看到当99%的元素是有序的时,我们比quicksort快5倍,当85%的元素是有序的时,我们快2倍。
当无序因素高于30%(低于70%的元素是有序的)时,Drop-Merge排序比其竞争对手慢。
算法细节
背景
由Abram Jackson和Ryan McCulloch撰写的论文《对Dropsort,一种损失性排序算法的改进》介绍了对神秘“损失性”排序算法Dropsort的改进。在Dropsort中,无序元素只是简单地“丢弃”(即删除)。在论文中,Jackson等人对Dropsort进行了改进,从而提高了对无序元素的检测,使得更多元素被保留,而丢弃的更少。
尽管论文没有明确指出,但它实际上描述了一个快速O(N)算法,用于寻找最长非递减子序列(LNS)问题的近似解。当列表中的大多数元素是有序的(LNS的一部分)时,该算法非常有效。
示例输入,其中大部分数据是有序的
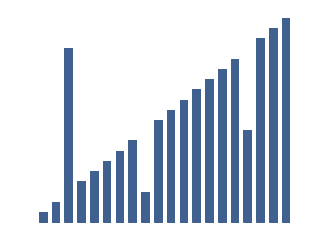
Drop-Merge排序
Drop-Merge排序的主要思想是这样的
- 使用Jackson等人论文中描述的方法来寻找最长非递减子序列(LNS)。
- 保留LNS并将异常值放入另一个列表中。
- 使用标准排序算法(在此实现中使用sort_unstable)对丢弃的异常值列表进行排序。
- 将异常值合并回已排序的LNS的主列表中。
因此,尽管其遗产如此,Drop-Merge排序是一种无损失的排序算法(即常规类型)。
寻找最长非递减子序列
实现使用了Jackson等人论文中的“内存”思想来检测“错误”——那些本应该被丢弃而不是被接受的元素。考虑以下数字序列
0 1 12 3 4 5 6 7 8 9
简单的Dropsort算法将接受0 1 12并丢弃其余的值(因为它们都小于12)。内存的思想是检测当我们连续丢弃了一定数量的元素时。当这种情况发生时,我们将回滚并丢弃最后一次长串丢弃之前的最后一个元素。这是一种回溯形式,解决了上述问题。在上述输入的情况下,算法将丢弃12并保留所有其他元素。在此实现中,我们考虑连续丢弃8个元素作为回滚和撤销的截止点。这包含了一个假设,即不会有超过8个异常值连续出现。这是一个在实践中表现很好的非常简单的方法。
Drop-Merge排序将保持有序元素的位置不变,将它们移动到列表的开始处。这有助于降低内存使用并提高性能。
如果元素是无序的,Drop-Merge排序可能比传统排序算法慢约10%。因此,Drop-Merge排序将尝试检测这种无序输入并中止,回退到标准排序算法。
与其他自适应排序算法的比较
自适应排序算法是一种可以利用现有顺序的算法。这些算法从复杂到简单都有。
在复杂的一端,有著名的Smoothsort,然而,它似乎相当不受欢迎——可能是因为其复杂性。我未能找到Smoothsort的良好实现,以便与Drop-Merge排序进行比较。Timsort是一种更现代且更受欢迎的自适应排序算法。它需要长序列的非递减元素才能与Drop-Merge排序的性能相媲美。标准的Rust排序使用Timsort的变体,从性能比较中可以看出,Drop-Merge排序在它设计的几乎排序的情况下获胜。
在简单的一端,有当只有一两个元素错位或列表非常短(最多几百个元素)时表现得非常好的O(N²)算法。例如包括插入排序和鸡尾酒排序。
Drop-Merge排序找到了一个有趣的平衡点——它相对简单(少于100行代码),但仍然能够在长列表上表现出良好的性能。然而,请注意,Drop-Merge排序依赖于另一个排序算法(例如快速排序)来对错位元素进行排序。
当Drop-Merge排序表现最佳时
- 少于20-30%的元素错位,并且这些错位元素在数据中随机分布(不是成群分布)。
- 您拥有大量数据(10k个元素或更多,当达到数百万时更是如此)。
限制和未来工作
Drop-Merge排序不是稳定的,这意味着它不会保持相等元素的顺序。
Drop-Merge排序不是原地排序,它将使用O(K)额外内存,其中K是错位元素的数量。
该算法使用recency=8,这意味着它一次最多只能处理8个连续的异常值。这个数字是通过实验选择的,也许可以根据性能进行动态调整。
其他实现
待办事项
- 设置TravisCI