3 个稳定版本
使用旧的 Rust 2015
| 1.0.2 | 2018年7月23日 |
|---|---|
| 1.0.1 | 2018年7月18日 |
#561 in 科学
9KB
Rust 中的范畴论
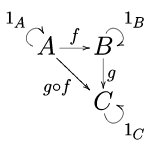

入门
我打算让每个小版本大致对应一个文档章节的增加。我将直到到达第二个 Milewski 课程,然后是第三个等,才提升主版本。
注意:这个 crate 更像是一个日志或笔记本,而不是一个功能库;请自行决定是否导入。
© 2018 Damien Stanton
查看 LICENSE 获取详细信息。
lib.rs:
或,对系统程序员而言的范畴论探索
本库中的内容源于 程序员范畴论,这是 Bartosz Milewki 持续多年的博客系列。从原始博客文章创建的“书籍”可以在 这里 找到。
crate 健康状况
目标
我的意图是通过使用 Rust 提供的内置文档和测试功能,简单地分享我对范畴论的学习经验。我还会进行屏幕录制来探索每个实现,以确保我提交到 crate 中的内容是合理的。我希望通过这样做,其他人可以将这些知识应用到他们在 C++、Go、Java 等语言中的工作中。
目录
| CTFP 章节 | 主题 | 文章 | 讲座视频 | 笔记 |
|---|---|---|---|---|
| 1 | 引言 | 范畴:组合的本质 | 动机,什么是范畴? | 见 id 和 compose |
非代码挑战问题
第 1 章
全球互联网在任何意义上都是一个范畴吗?链接是态射吗?
我会说是的。我们知道网页有类似恒等态射的东西:其 URI/URL。页面之间的链接可能是可组合的(从一个站点 A 到 B 的链接可以通过重定向协议映射到第三个站点 C)。
更新:在与 FP Slack 上的 #categorytheory 频道中的几个人交谈后,我们必须注意,我们指的是定义链接在整个 REST 或 HATEOAS 命令周期中的态射,而不是链接本身。因此,Bartosz 的正确答案取决于我们如何定义 links。
Facebook是否是一个范畴,其中人以对象出现,友谊以态射出现?
并非如此,因为社会关系并不总是可以组合的。C是B的朋友,但这并不意味着C一定是A的朋友。
什么时候一个有向图是一个范畴?
如果图 G 有顶点 V 和边 E,并且满足以下条件,则有向无环图(DAG)可以归类为范畴:
- 图中所有路径都可以连接起来
- 每个顶点V都有一个边E可以回到自己(从而满足恒等性)
