8个版本 (稳定版)
| 1.1.6 | 2024年4月11日 |
|---|---|
| 1.1.5 | 2024年4月9日 |
| 0.1.0 | 2024年4月4日 |
在游戏分类中排名77
每月下载34次
22KB
237 行
Copy Cards
这是什么?
这是一个我们需要共同完成的项目,我们需要创建一个赌场游戏并计算其背后的所有复杂数学。
游戏规则
玩家从关闭的盒子中抽取一张牌。这张牌会被记录然后放回。玩家总共抽取10次。如果抽到重复的牌,则玩家输掉游戏,如果没有发生这种情况,则玩家获胜。抽到3张牌后,玩家可以选择加倍下注。如果玩家获胜,他们将获得双倍的下注金额,如果玩家失败,赌场将保留这笔钱。
概率
生日悖论
这个游戏基于生日悖论。直观上,你可能需要很多人才能有50%的几率两个人分享相同的生日。然而,只需要23个人。计算这个的公式是:$P(c)=1-\frac{n!}{(n-k)!\cdot n^{k}}$。在这个公式中,$n$ 是生日的数量(通常是365),而 $k$ 是人的数量。
期望值
使用前面的公式,我们可以计算期望值。$$P(c)=1-\frac{52!}{(52-10)!\cdot52^{10}}\approx60.2\%$$ 抽到3张牌后,玩家可以加倍下注。这是在加倍之前、加倍之后和玩家获胜时赌场获胜的概率。$$P(c_{1-3})=1-\frac{52!}{(52-3)!\cdot52^{3}}\approx5.7\%$$ $$P(c_{4-10})=1-((1-\frac{52!}{(52-3)!\cdot52^{3}})+\frac{52!}{(52-10)!\cdot52^{10}})\approx54.6\%$$ $$P(p)=\frac{52!}{(52-10)!\cdot52^{10}}\approx39.7\%$$
金钱
因此,赌场大约赚取:$$m(g,s,d)=g\cdot(s\cdot0.056+s(b+1)\cdot0.547-s(b+1)\cdot.397)$$ 其中 $m$ 是金钱,$g$ 是游戏数量,$s$ 是赌注,$d$ 是玩家是否加倍(这是一个布尔值,0或1)。想象一下这个游戏被玩了10,000次,玩家每次在抽到第三张牌时都加倍下注。他的初始赌注是10欧元。$$m(10000,10,1)=10000\cdot3.56=€35600$$
正态分布
让我们再玩10,000次。当 $n$ 接近无穷大时,我们可以假设
$$\mathcal{B}(n,p)\sim\mathcal{N}(np,\sqrt{np(1-p})$$ 现在我们可以计算 $\mu$ 和 $\sigma$ 的值。
$$\mu=np=10000\cdot0.602=6020$$
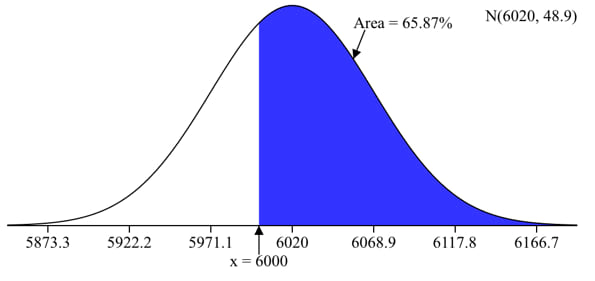
$$\sigma=\sqrt{np(1-p)}=\sqrt{10000\cdot0.602\cdot(1-0.602)}\approx48.9$$ 我们可以使用这个来绘制一个图表。
我们可以看到,有65.9%的几率赌场在10,000场比赛中赢得6000场或更多。
安装
要玩这款游戏,您需要执行以下操作之一:
访问 发行版 并下载与您的操作系统对应的文件。
您也可以使用 cargo 安装游戏。请注意,您确实需要安装 Rust。
cargo install copy-cards
如果这样不行,或者您想本地构建,请按照以下步骤操作。这也需要安装 Rust。
git clone https://github.com/7ijme/copy-cards
cd copy-cards
cargo build --release
现在您可以玩游戏了,祝您玩得开心!
依赖项
~6–12MB
~123K SLoC