12个版本
| 0.1.11 | 2024年7月4日 |
|---|---|
| 0.1.10 | 2023年6月4日 |
| 0.1.3 | 2023年5月31日 |
| 0.1.1 | 2023年4月26日 |
#234 in 算法
237 每月下载量
用于 2 crates
590KB
4K SLoC
AUTOmata Utilities and Representation (AUTOUR)
法语中,“Autour”这个词指的是一种鸟。它在英语中对应“Goshawk”。
Autour 是一个小型工具箱,用于实验各种自动机和正则表达式。该项目更注重教学而不是性能。它仍在开发中。
形式
自动机形式如下
- 确定性有限自动机 (DFA)
- 非确定性有限自动机 (NFA)
- 具有即时转换的非确定性有限自动机 (NFAIT)(即具有ε转换)
- 具有基本正则表达式 (BRE) 标记转换的广义非确定性有限自动机 (GNFA)(尚未完全集成)
我们还可以操作正则表达式
- 基本正则表达式 (BRE)
- 扩展正则表达式 (ERE)(尚未完全集成)
特性
可以使用 graphviz_dot_builder crate 使用 GraphViz 绘制自动机。
以下我们将使用这些图形表示法来介绍工具箱的一些功能。
转换
不同形式之间的转换是可能的。在下面的示例中,我们将一个 GNFA 转换为(从左到右)一个 DFA、一个 NFAIT 和一个 BRE。
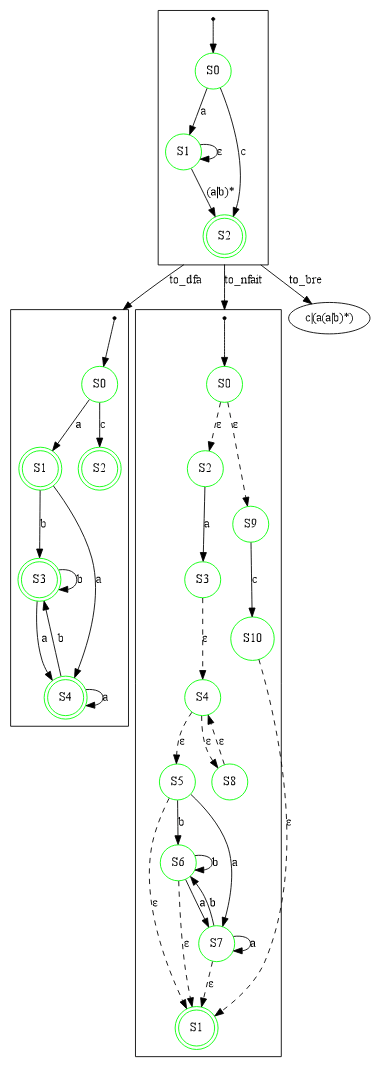
(共)可达性
各种算法允许
- 确定自动机是否可达
- 使自动机可达
- 确定自动机是否是共可达的
- 使自动机共可达
- 确定自动机是否是共可达的
- 使自动机共可达
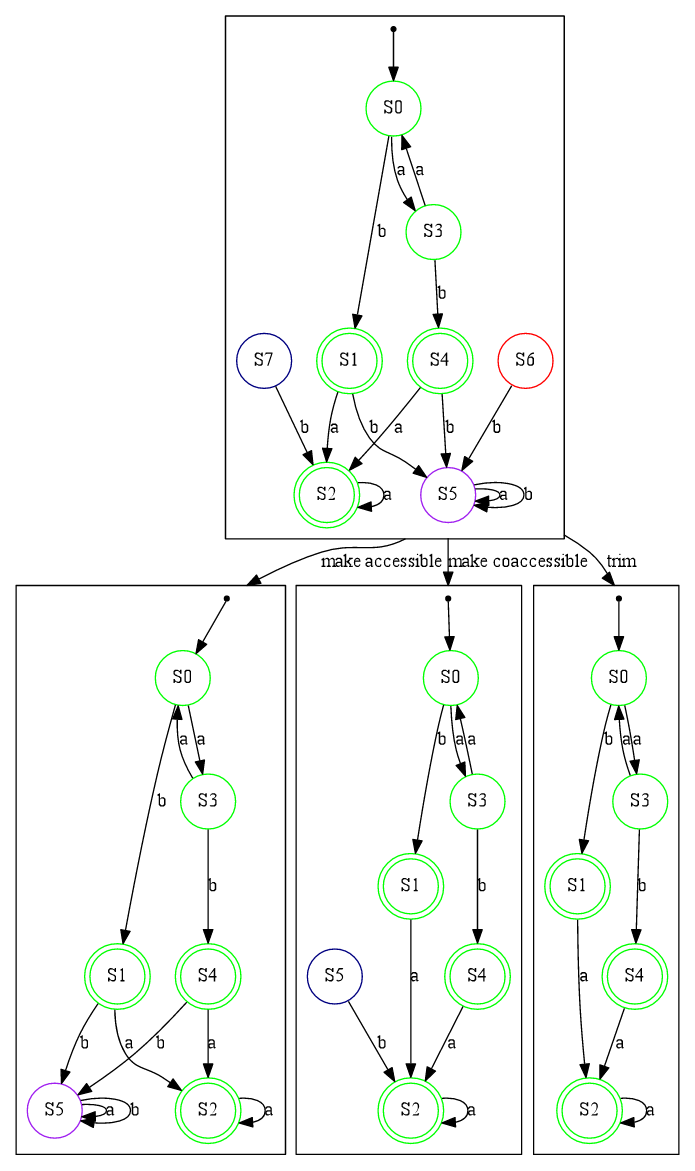
以下示例中,我们有一个最初表示在图像顶部的初始 DFA。
- 绿色节点既是可达的也是共可达的。
- 紫色节点是可达的,但不是共可达的。
- 蓝色节点是共可达的,但不是可达的。
- 红色节点既不可达也不共可达。
然后我们通过以下方式转换这个初始 DFA(从左到右)
- 使其可达
- 使其共可达
- 修剪它,即使其既可达又共可达
构建自动机
构建术语的方法
- 并集
- 交集
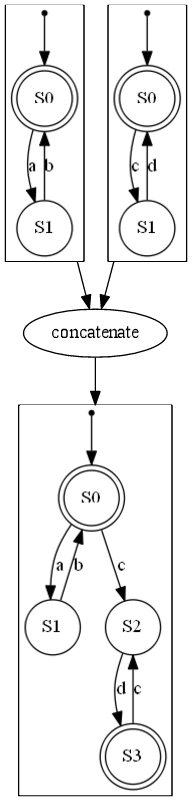
- 连接
- 重复
- 否定
- 反转
- 等等
以下是一些示例
| DFA 连接 | DFA Kleene | DFA 反转 | DFA 交错 | DFA 合并 |
 |
 |
 |
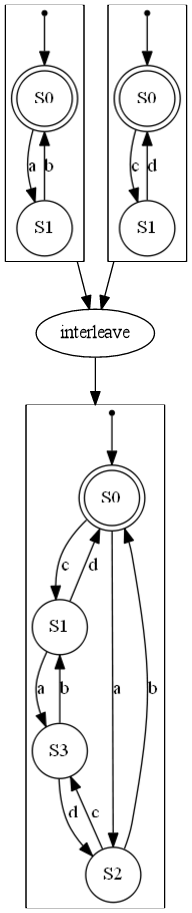 |
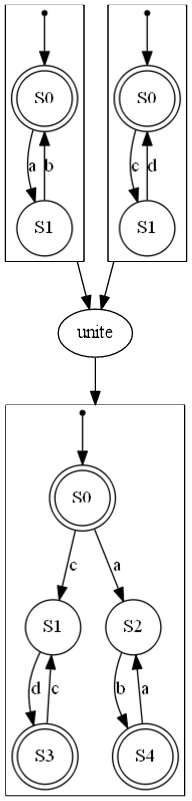 |
| NFA 合并 | NFA 交集 |
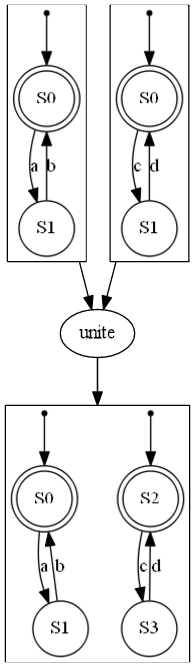 |
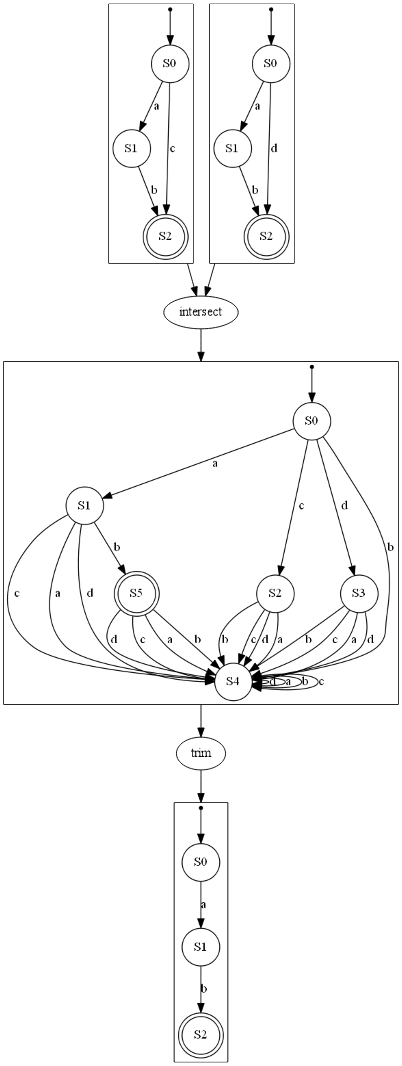 |
自动机最小化
DFA
DFA 最小化是通过 Brzozowski 算法实现的(反转的反转)。
以下是一个示例
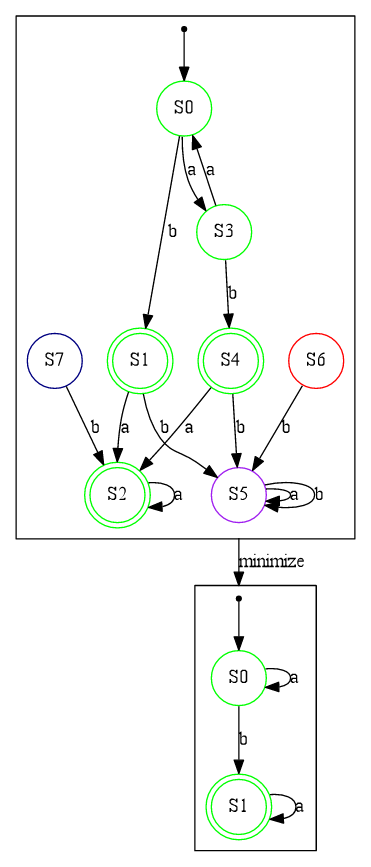
NFA
NFA 最小化是通过 Kameda-Weiner 算法实现的。以下展示了两个示例,详细描述了该过程。
第一个示例
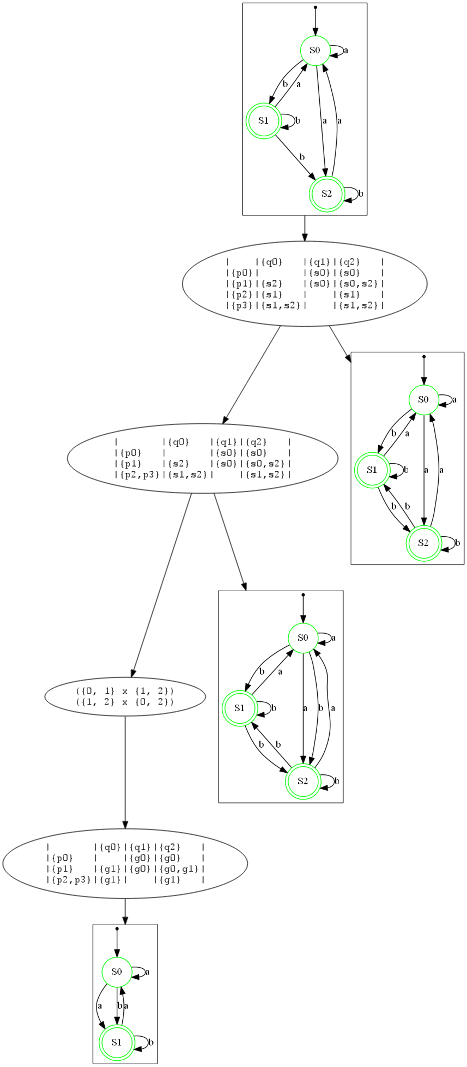
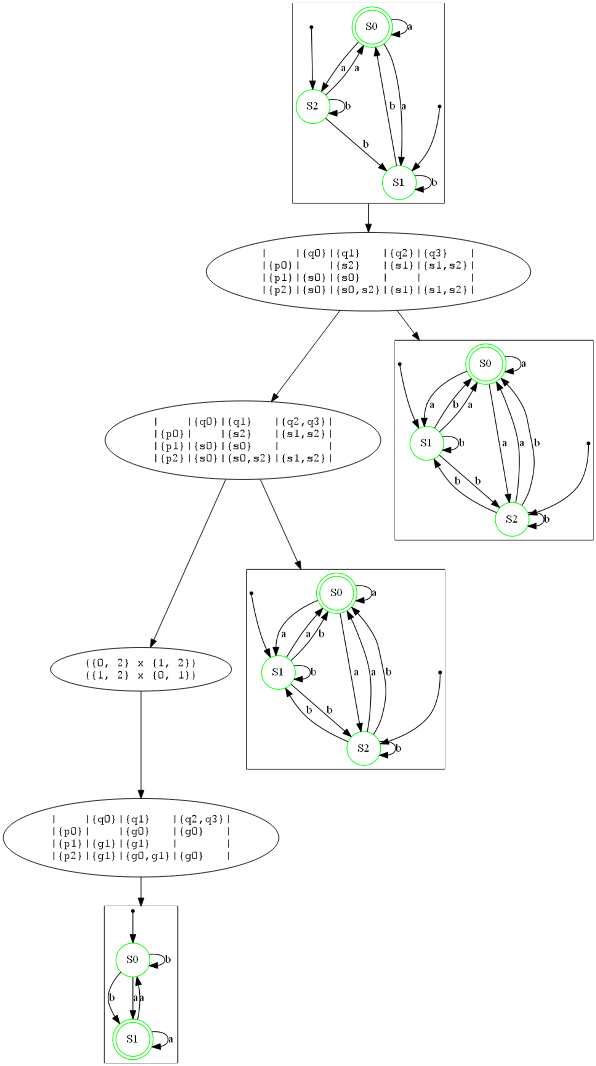
第二个示例是接受与第一个示例相对的反向语言 NFA(你可以注意到两个示例矩阵在行和列位置替换后的对称性)
字母隐藏和替换
我们还可以替换字母或隐藏它们。
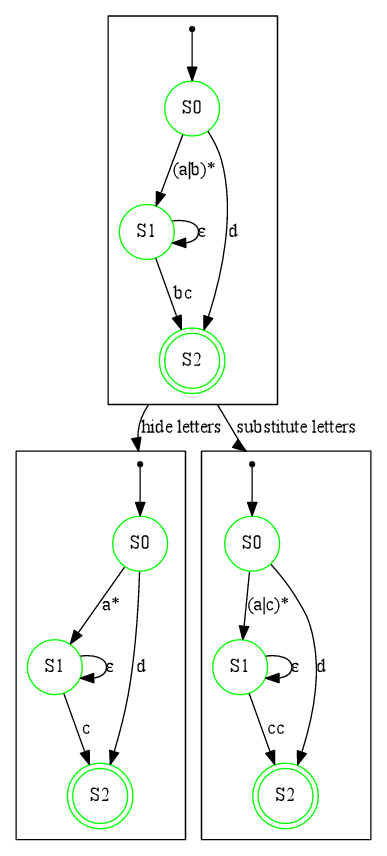
在下面的示例中,我们有一个初始 GNFA 在图像顶部绘制。然后,从左到右
- 我们在其中隐藏字母 'b'
- 我们在其中将字母 'b' 替换为字母 'c'
其他功能
- 字母表完成
- DFA/NFA 中的运行转换和轨迹
- 等等
依赖项
~1.3–1.8MB
~39K SLoC